Гетерогенные каталитические реакторы. Влияние диффузии внутри пор на селективность. Дезактивация катализатора, страница 6

получается интегрированием (1.50). Чтобы это сделать, запишем:

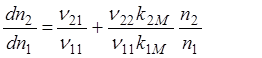
При n₂₀ = 0, промежуточное вещество А₂ в реактор не вводится:

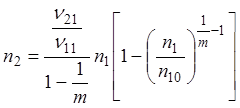
или

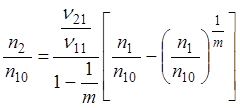
и, т.к. n₁=n₁₀(1-X₁)

При этих условиях:

                                        (1.52)

и

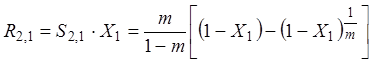
Если обе реакции существенно зависят от диффузии внутри пор, можно показать, что:

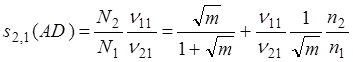                               (1.53)

где

N₂       = молярный поток А₂, покидающий,

N₁           = молярный поток А₁, поступающий в гранулу,

n₁₁/n₂₁ = отношение двух потоков в идеальной ситуации.

Зная также, что:

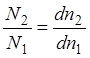
мы можем вычислить интегральную селективность (в соответствии с определением)

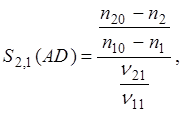
исходя из того, что

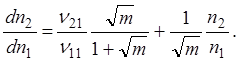
Интегрируя в предположении, что n₂₀ = 0, можно получить:

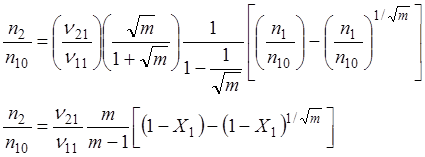
и, соответственно,

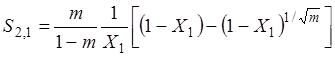                                   (1.54)

и

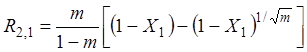
Если m больше 1, что часто имеет место, селективность при наличии диффузионных ограничений ниже. Для m»10 селективность снижается приблизительно на 50%. Уменьшение размера частицы позволяет устранить эти потери, по крайней мере, частично.

При отсутствии диффузионных ограничений в соответствие с (1.50). В самом начале реакции можно ожидать появления только А₂, реакция 2 практически отсутствует, селективность =1. (случай без диффузионных ограничений)

В случае наличия диффузионных ограничений, можно видеть, что начальная селективность равна . Это означает, что в начале реакции продукт А₃ заметно образуется из А₂. Это четко указывает на то, что А₂ задерживается в порах и не может выйти из пор без ущерба. Этот анализ может использоваться для решения вопроса о диффузионных ограничениях.

1.7. Оценка коэффициента диффузии D_e

Если поры относительно большие и давление достаточно велико (Р>>1 атм.), можно применять приближенное соотношение для D_e. Это модифицированное уравнение для коэффициента диффузии в гомогенной фазе, скорректированное с учетом доли объема пор в частицах:

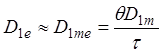                                                                   (1.55)

где

 - может быть оценено на основе соотношений для молекулярной диффузии в газе или  в жидкости,

 - пористость приводится в данных о грануле,

t - изменяется от 2 до 10: при отсутствии точных данных, можно считать, что t изменяется от 2 до 4.

В случае очень малых пор и низких давлений условия могут не соответствовать характерным для гомогенной фазы. Т.к. средняя длина свободного пробега молекул велика, а расстояние между стенками поры малы, молекулы смогут двигаться преимущественно вдоль поры. Этот диффузионный режим называется Кнудсеновским режимом, а вычисления коэффициента диффузии проводятся на основе кинетической теории газов. Считая, что средняя длина свободного пробега равна диаметру поры, можно получить, что:

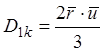                                                           (1.56)

где

=средний радиус пор,

=средняя скорость молекулы:

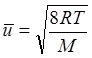 (в соответствии с кинетической теорией газов)

Так как:

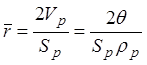                                                     (1.57)

можно получить:

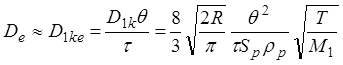                                             (1.58)

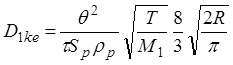                                                       (1.59)

где

q = пористость (безразмерный),

t = коэффициент (безразмерный),

S_p = удельная поверхность (м³/кг)

r_р = плотность частицы (кг/м³)

Т = температура (К)

М₁ = молекулярный вес (кг/моль)

R = 8.31 (Дж/(моль×К)),

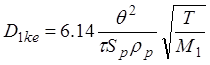(м²/с)                                       (1.60)

если М выражается в г/моль, как обычно

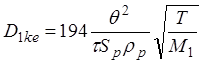                                                (1.61)

Порядок величин

Т = 600 К

М₁ = 200 г/моль

q = 0.5

t = 2

S_p = 200 м²/г или 2×10⁵ м²/кг

r_р = 1500 (кг/м³)

S_pr_р = 3×10⁸ м^-1

м²/с

Если D_1m/ D_1к>>1, D_1e» D_1к. Если D_1m/ D_1к <<1, D_1e» D_1m. В промежуточном случае используется среднее значение D_1e, определяемое на основе соотношения:

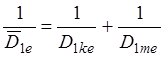                                                      (1.62)

1.8  Влияние внешнего массопереноса.

Концепция общей эффективности.

1.8.1. Суммарный (общий) коэффициент переноса