Гетерогенные каталитические реакторы. Влияние диффузии внутри пор на селективность. Дезактивация катализатора, страница 4

(b) Если n₂ < (- n₁), эффективность возрастает.

Викман и Горинг ввели модуль изменения объема:

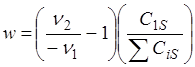                                                         (1.42)

где

С_1S = концентрация А₁ на внешней поверхности гранулы

SС_iS = сумма всех концентраций, включая инерт на внешней поверхности гранулы, выполнили анализ изменения отношения эффективности h_v (неизохорические условия) к h (изохорические условия) для различных величин порядка реакции, модуля Тиле и модуля w. На основе их результатов можно заключить, что 0,7<h_v /h<1,3, для характерных (обычных) величин:

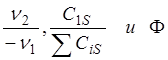                                                       (1.43)

На основании изложенного можно заключить, что неизохоричность редко является важным фактором, особенно, если учесть неточность в определении эффективного коэффициента диффузии.

1.5.4. Неизотермические реакции

Легко представить, что при протекании экзотермических реакций в грануле будет выделяться тепло, которое необходимо удалить из гранулы. Если тепло не полностью удаляется из гранулы, то это ведет к увеличению Т и скорости реакции. В зависимости от тепловыделения и теплопроводности гранулы внутри нее будет устанавливаться температурный градиент. Средняя температура гранулы будет выше в случае экзотермической реакции и ниже – в случае эндотермической реакции, чем температура на поверхности.

Важнейшие параметры в данном случае – это:

(а) Теплота реакции DН_R (Дж/моль)

(b) Энергия активации реакции Е (Дж/моль)

(с) Концентрация реактанта на поверхности С_1S (моль/м³) (С_1R – для сферической гранулы)

(d) Эффективная теплопроводность пористой гранулы l_е (Вт/(м×к))

(е) Температура поверхности Т_S (К)

(f) Коэффициент диффузии реактанта в пористой среде D_1е (м²/с)

Эти параметры могут быть сгруппированы в следующие безразмерные комплексы:

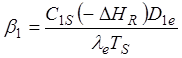  число Пратера                                      (1.44)

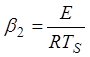 число Аррениуса                                                      (1.45)

где R – газовая постоянная (8,31 Дж/(моль×К))

необходимо повторить, что эффективность это отношение кажущейся скорости реакции в грануле, к теоретической скорости реакции, соответствующей температуре Т_S и концентрации С_1S. При этом, в соответствии с определением, вполне естественно получить эффективность существенно больше 1.

Для b₁<0, эффективность всегда меньше 1. Это соответствует эндотермической реакции. Для b₁>0 (экзотермическая реакция), имеют место два противоположных эффекта. Средняя температура гранулы может быть значительно выше Т_S, а средняя концентрация , наоборот, меньше, чем С_1S. Поэтому, в зависимости от величин Ф, b₁ и b₂, величина может быть ниже или выше 1.

При постоянных Т_S и b₁ увеличение b₂, происходящее за счет увеличения Е, ведет к увеличению эффективности (большая чувствительность к изменению температуры). Величины b₁ и b₂ могут изменяться в следующих пределах.

Физический смысл параметра b₁

Исходя из баланса энергии для сферического слоя толщиной d_z для стационарных условий,  можно получить:

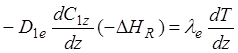                                                   (1.46)

Если l_е, D_1е и DH_R считать постоянными, то это выражение можно проинтегрировать и получить:

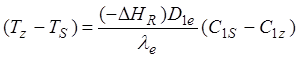                                                       (1.47)

Принимая во внимание, что минимальное значение С_1z равно 0, для максимального перехода температуры в грануле можно записать:

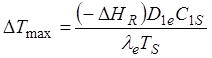
Откуда

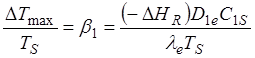                                                     (1.48)

Следовательно, b₁ максимальное относительное увеличение (снижение) температуры в грануле.

Если:

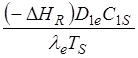
меньше 5К, то влиянием температуры на эффективность можно пренебречь.

Для Т_S = 500К, это соответствует b₁= 0.01.

Главная трудность в оценке b₁ состоит в оценке величины D_e и, особенно, l_е. Рис. 1.4 иллюстрирует изменение эффективности в зависимости от модуля Тиле и числа Пратера b₁, для b₂=20, соответствующего характерному случаю. Из рисунка видно, что