Булевы функции. Основные формулы булевой алгебры. Аналитическая запись булевых функций в булевом базисе. Дешифраторы. Мультиплексоры, страница 7

Одно из основных требований к системе логических элементов, состоит в том, чтобы из элементов этой системы можно было  построить любую логическую схему. Техническая задача отыскания такой системы элементов сводится к математической задаче определения набора функций, из которых методом суперпозиции можно получить любую функцию.

Система булевых функций называется функционально полной, если произвольную булеву функцию можно представить суперпозицией функций этой системы.

Для решения задачи были выделены пять классов булевых функций:

- сохраняющие нуль – это функции равные нулю на нулевом наборе аргументов: ;

- сохраняющие единицу – это функции равные единице на единичном наборе:

;

- самодвойственные булевы функции на каждой паре противоположных наборов принимают противоположные значения: ;

- линейные булевы функции - это функции, которые можно представить линейным полиномом: , где .

Если значения каждого аргумента одного набора больше или равно значению того же аргумента второго набора, то говорят, что первый набор не меньше второго. Следует заметить, что не все наборы являются сравнимыми, например (1,0,1) и (0,1,0) не сравнимы.

- монотонной булевой функцией называют функцию, у которой при любом возрастании набора аргументов значения функции не убывают.

Доказана теорема о функциональной полноте: для того чтобы система булевых функций была функционально полной, необходимо и достаточно, чтобы эта система включала:

- хотя бы одну функцию, не сохраняющую нуль;

- хотя бы одну функцию, не сохраняющую единицу;

- хотя бы одну нелинейную функцию;

-хотя бы одну немонотонную функцию;

-хотя бы одну несамодвойственную функцию.

В таблице показано, к каким классам относятся функции двух аргументов:

При рассмотрении таблицы можно выделить 44 функционально полных системы булевых функций: 2 – одно функциональных, 16 – двух функциональных, 23 –трех функциональных, 3 – четырех функциональных.

Система функций, которая является функционально полной, называется базисом.

Минимальным базисом называется такой базис, удаление из которого хотя бы одной функции превращает систему в неполную.

В настоящее время используются три базиса - базис Шеффера, базис Пирса и булев базис, в котором содержатся три функции И, ИЛИ, инверсия.

Заметим, что булев базис не является минимальным, т.к. из него можно удалить либо функцию И, либо функцию ИЛИ.

Аналитическая запись булевых функций в базисе Пирса.

Будем использовать следующее обозначение:

.

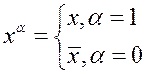Вспомним запись булевой функции в совершенной дизъюнктивной нормальной форме: . Символ  означает, что дизъюнкция берется только для таких наборов  на которых функция равна единице: . Попробуем записать эту функцию таким образом, чтобы оно содержало только функции Пирса и отрицания (отрицание также реализуется функцией Пирса: ). Просуммируем конституенты единицы наборов, где функция равно нулю. Мы получили новую функцию, значения которой противоположны исходной  функции, поэтому: 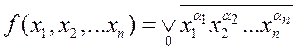.  Но последнее выражение есть не что иное, как функция Пирса: 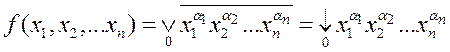 .  Однако конституенты единицы представляют собой конъюнкции переменных и от конъюнкций нужно также избавиться. Для этого преобразуем конституенты единицы: .