Если контур занимает половину таблицы, то над аналитическим описанием этого контура ставится дополнительное отрицание;
Если в таблице только один контур, то над ним также следует поставить дополнительное отрицание.
Естественно, если в таблице только один контур, и он занимает половину таблицы, то над ним ставятся два дополнительных отрицания.
Пример: минимизировать в базисе Пирса функции:
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
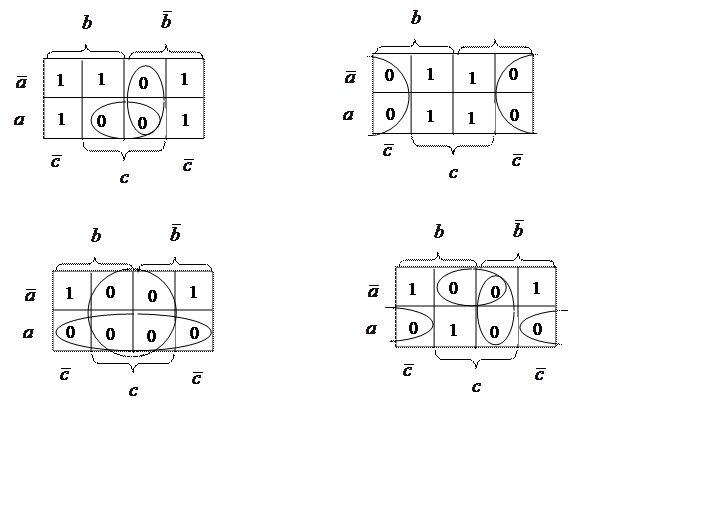
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Очевидно Вы заметили, что правила заполнения и обводки
одинаковы при минимизации в базисе Пирса и при получении минимальных
конъюнктивных нормальных форм. Следовательно, МКНФ можно получить из этих же
таблиц:![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Минимизация булевых функций большого числа аргументов.
Для минимизации булевых функций большого числа аргументов могут быть использованы различные методы: метод неопределенных коэффициентов, метод минимизирующих карт, метод Квайна – Мак-Класки и т.д. Многие из методов страдают громоздкостью записи при их использования, некоторые работают только с полностью определенными булевыми функциями, а большинство методов позволяет получить только минимальные дизъюнктивные нормальные формы.
Рассмотрим идею простейшего метода минимизации функций произвольного числа аргументов, который легко программируется и пригоден для минимизации не полностью определенных булевых функций. Используя эту идею легко получить алгоритмы минимизации булевых функций не только в МДНФ и МКНФ, но и в базисах Пирса и Шеффера.
В начале рассмотрим получение МДНФ.
Минимизация булевых функций методом подбора
кратчайших претендентов.
При использовании метода булева функция представляется матрицей наборов аргументов, на которых функция равна единице (матрица единиц) и матрицей наборов, на которых функция равна нулю (матрица нулей). Под претендентом будем понимать в зависимости от требуемой формы представления функции произведение, сумму, функцию Шеффера, либо функцию Пирса над аргументами, взятые с отрицанием, либо без него. При получении МДНФ претендент – произведение аргументов. При получении МКНФ претендент – сумма аргументов, при минимизации в базисах Шеффера и Пирса – претендент операция И-НЕ и ИЛИ-НЕ над аргументами.
Число аргументов претендента будем называть длиной претендента.
Рассмотрим метод получения МДНФ методом подбора кратчайших произведений.
Пример. Задана не полностью определенная булева функция
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
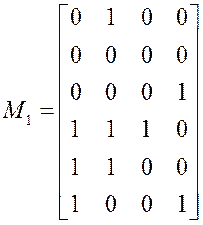 ,
,
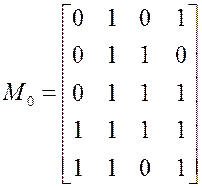
Берем первый набор матрицы единиц 0100.
Произведения, покрывающие этот набор, рассматриваются как претенденты на
вхождение в минимальную форму: ![]()
![]() - не подходит, поскольку оно
равно 1 не только на 0100 матрицы единиц, но и на наборах 0101, 0110, 0111
матрицы нулей;
- не подходит, поскольку оно
равно 1 не только на 0100 матрицы единиц, но и на наборах 0101, 0110, 0111
матрицы нулей;
![]() - не подходит, поскольку равно 1
на всех наборах матрицы нулей;
- не подходит, поскольку равно 1
на всех наборах матрицы нулей;
![]() -не подходит, т.к. равно 1 на
наборах 0101, 1101 матрицы нулей;
-не подходит, т.к. равно 1 на
наборах 0101, 1101 матрицы нулей;
![]() - не подходит, т.к. равно 1 на
наборе 0110;
- не подходит, т.к. равно 1 на
наборе 0110;
![]() -не подходит, т.к. равно 1 на
наборе 0101, 0110, 0111;
-не подходит, т.к. равно 1 на
наборе 0101, 0110, 0111;
![]() - не подходит, т.к. равно 1 на
наборе 0101;
- не подходит, т.к. равно 1 на
наборе 0101;
![]() - не подходит, т.к. равно 1 на
наборе 0110;
- не подходит, т.к. равно 1 на
наборе 0110;
![]() - не подходит, т.к. равно 1 на
наборах 0101 и 1101;
- не подходит, т.к. равно 1 на
наборах 0101 и 1101;
![]() - не подходит, т.к. равно 1 на
наборе 0110;
- не подходит, т.к. равно 1 на
наборе 0110;
![]() -подходит, поскольку не равно 1 ни на одном наборе матрицы нулей и покрывает
наборы 0100, 0000 матрицы единиц.
-подходит, поскольку не равно 1 ни на одном наборе матрицы нулей и покрывает
наборы 0100, 0000 матрицы единиц.
Вписываем ![]() в МДНФ
и удаляем наборы 0100 и 0000 из матрицы единиц:
в МДНФ
и удаляем наборы 0100 и 0000 из матрицы единиц: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.