Доказательство. Выбираем в таблице
истинности произвольный набор. Если на этом наборе функция равна нулю, то
записываем конституенту нуля равную нулю на этом наборе. Поскольку свойство
конъюнкции ![]() , то на данном наборе функция будет равна
нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на
этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны
1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной
совершенной нормальной формой (КСНФ).
, то на данном наборе функция будет равна
нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на
этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны
1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной
совершенной нормальной формой (КСНФ).
Алгоритм перехода к КСНФ:
-Выбрать в таблице истинности наборы на которых функция равна нулю.
-Записать конституенты нуля равные нулю на этих наборах. Для этого, если аргумент набора равен нулю, то он входит в конституенту без отрицания, если же аргумент входит в набор как 1, то в соответствующую конституенту нуля вписывается его отрицание.
-Все записанные конституенты нуля соединяем знаком конъюнкции.
Запишем КСНФ для функции из предыдущего примера:
![]() .
.
Дешифраторы.
При работе с дискретными устройствами приходится решать задачи анализа схем и задачи синтеза схем. При решении задачи синтеза после получения технического задания на проектирование устройства составляется математическая модель устройства, а затем разрабатывается схема устройства. Задача анализа обратная задаче синтеза. Решим задачу анализа, рассматривая схему простейшего дешифратора с прямыми выходами.
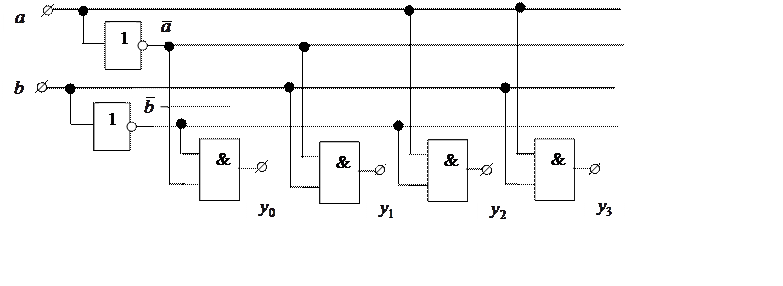
В схеме два входа ![]() ,
, ![]() и четыре выхода, которые описываются
булевыми уравнениями:
и четыре выхода, которые описываются
булевыми уравнениями: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Построим таблицы истинности для этих уравнений:
. Построим таблицы истинности для этих уравнений:
|
|
|
|
|
|
|
||
|
0 |
0 |
1 |
0 |
0 |
0 |
||
|
0 |
1 |
0 |
1 |
0 |
0 |
||
|
1 |
0 |
0 |
0 |
1 |
0 |
||
|
1 |
1 |
0 |
0 |
0 |
1 |
Итак, если на вход дешифратора подать аргументы
булевой функции, то на выходах дешифратора можно получить все конституенты 1.
Число входов дешифратора ![]() связано с числом
выходов
связано с числом
выходов ![]() соотношением
соотношением ![]() .
Дешифраторы с двумя, тремя, четырьмя и т.д. входами можно рассматривать как
генераторы конституент единицы для функций 2, 3, 4, и т.д. аргументов. Суммируя
конституенты 1 для наборов, где функция равна 1, мы получаем реализацию этой
функции.
.
Дешифраторы с двумя, тремя, четырьмя и т.д. входами можно рассматривать как
генераторы конституент единицы для функций 2, 3, 4, и т.д. аргументов. Суммируя
конституенты 1 для наборов, где функция равна 1, мы получаем реализацию этой
функции.
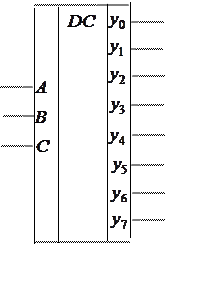 Приведем условные графические
обозначения ( УГО) дешифраторов с 2 и 3 входами:
Приведем условные графические
обозначения ( УГО) дешифраторов с 2 и 3 входами:
 |
Пример: реализовать систему булевых функций на дешифраторе с прямыми выходами.
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
* |
|
0 |
1 |
0 |
* |
0 |
1 |
1 |
0 |
1 |
* |
|
0 |
1 |
1 |
* |
0 |
1 |
1 |
1 |
0 |
0 |
Функции ![]() и
и ![]() зависят от трех аргументов, следовательно,
необходим дешифратор с тремя входами. Особенностью этих функций является то,
что они заданы не на всех наборах. Такие функции называют не полностью
определенными булевыми функциями. Наборы, на которых функция не определена,
помечены символом *. Эти функции необходимо доопределить, т. е. приписать
функциям нам этих наборах значения 0 или 1.
зависят от трех аргументов, следовательно,
необходим дешифратор с тремя входами. Особенностью этих функций является то,
что они заданы не на всех наборах. Такие функции называют не полностью
определенными булевыми функциями. Наборы, на которых функция не определена,
помечены символом *. Эти функции необходимо доопределить, т. е. приписать
функциям нам этих наборах значения 0 или 1.
Доопределение проводят таким образом, чтобы получить наиболее простую схему. Для данного примера выгодно доопределить эти наборы нулями.
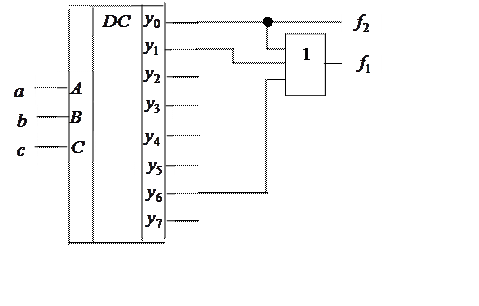 |
Существуют дешифраторы с инверсными выходами. Схема такого дешифратора имеет вид:
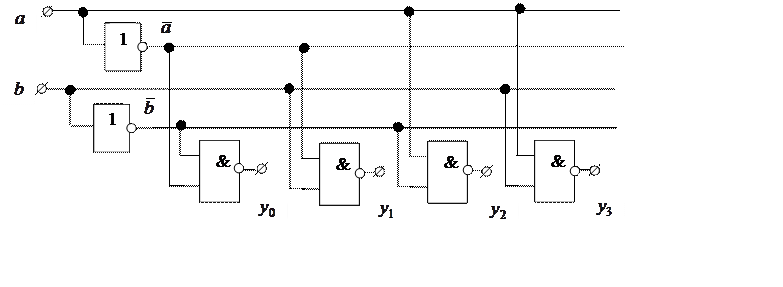 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.