Булевы функции. Основные формулы булевой алгебры. Аналитическая запись булевых функций в булевом базисе. Дешифраторы. Мультиплексоры, страница 16

Нетрудно подсчитать, что число слов в каждой из матриц при минимизации функций 32 аргументов на 32-разрядных машинах составит 134217728. Такой объем оперативной памяти доступен для современных ЭВМ. Главными ограничениями метода являются приемлемое время ввода значений функции и время собственно минимизации функции. Однако не следует смотреть на проблему минимизации слишком пессимистично, т.к. известно, что реальные булевы функции большого числа аргументов в подавляющем большинстве случаев не определены, причем число неопределенных наборов возрастает с ростом числа аргументов булевой функции. 

Синтез комбинационных схем

Существует класс логических устройств,  у которых выходные сигналы схемы в данный момент времени зависят только от комбинации входных сигналов поступивших на схему в данный момент времени:

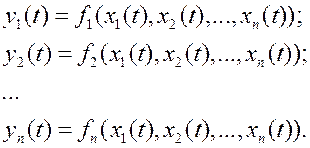
Такие схемы называют комбинационными. Они описываются системой булевых функций.

Задача синтеза обратна задаче анализа. Для решения задачи синтеза схема должна быть представлена  так называемым техническим заданием. В этом задании, каким – либо  способом формулируют основные технические требования, предъявляемые к устройству. Обычно это  текстовое описание, при необходимости сдобренное таблицами, графиками, формулами и.т.п. В нем иногда отражают типы логических элементов, на которых реализуется устройство. Как правило, это задание неоднозначно описывает это устройство и поэтому первым шагом синтеза является построение математической модели устройства, в которой эти неоднозначности исключены. Это трудно формализуемый этап, поэтому эту задачу обычно решают самые квалифицированные сотрудники коллектива разработчиков.

Если синтезируется комбинационная схема, то последующие этапы это

- упрощение математической модели (минимизация системы булевых функций в заданном базисе);

- построение функциональной схемы устройства;

- преобразование функциональной схемы в принципиальную схему. (Это преобразование Вы сможете проводить после изучения курса «Схемотехника»).         

Задача. Разработать схему одноразрядного двоичного сумматора. При реализации схемы использовать элементы И-НЕ.

Можно попытаться изобрести эту схему, а можно её синтезировать. Ничего не имея против изобретательства, отмечаю, что кесарю – кесарево.

Если Вы хотите создать вечный двигатель, то его нужно изобретать (хотя некоторые негодяи считают, что это невозможно), но если Вы разрабатываете логическую схему, то ее нужно синтезировать.

          Попытаемся составить математическую модель устройства. Это устройство явно принадлежит к классу комбинационных схем, т.к. сумма определяется значением слагаемых. Определимся с числом входов и выходов схемы:

Зачем нужен одноразрядный сумматор? Очевидно для  изготовления многоразрядного сумматора. Но при суммировании многоразрядных слов необходимо учитывать перенос из предыдущего младшего разряда, поэтому входов должно быть три: на два  входа  и  подаются разряды слагаемых, а на третий вход   – перенос из предыдущего разряда. 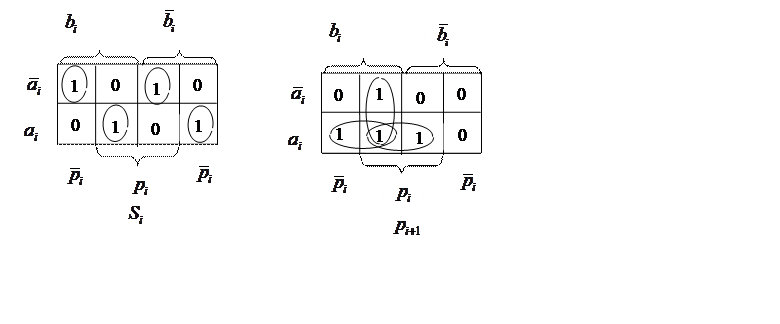Выходов у схемы два, на выходе  формируется значение суммы в данном разряде, а на выходе  – значение переноса в следующий разряд. Зная правила двоичной арифметики, составляем таблицы истинности этих функций:

Минимизируем эти функции в базисе Шеффера (И-НЕ):

;

.

Достаточно часто при изображении схем используют так называемый жгут. Жгут – это изображение множества проводников одной жирной линией. Естественно, что провода входящие в жгут и выходящие из него должны маркироваться.

Изобразим функциональную схему одноразрядного сумматора:

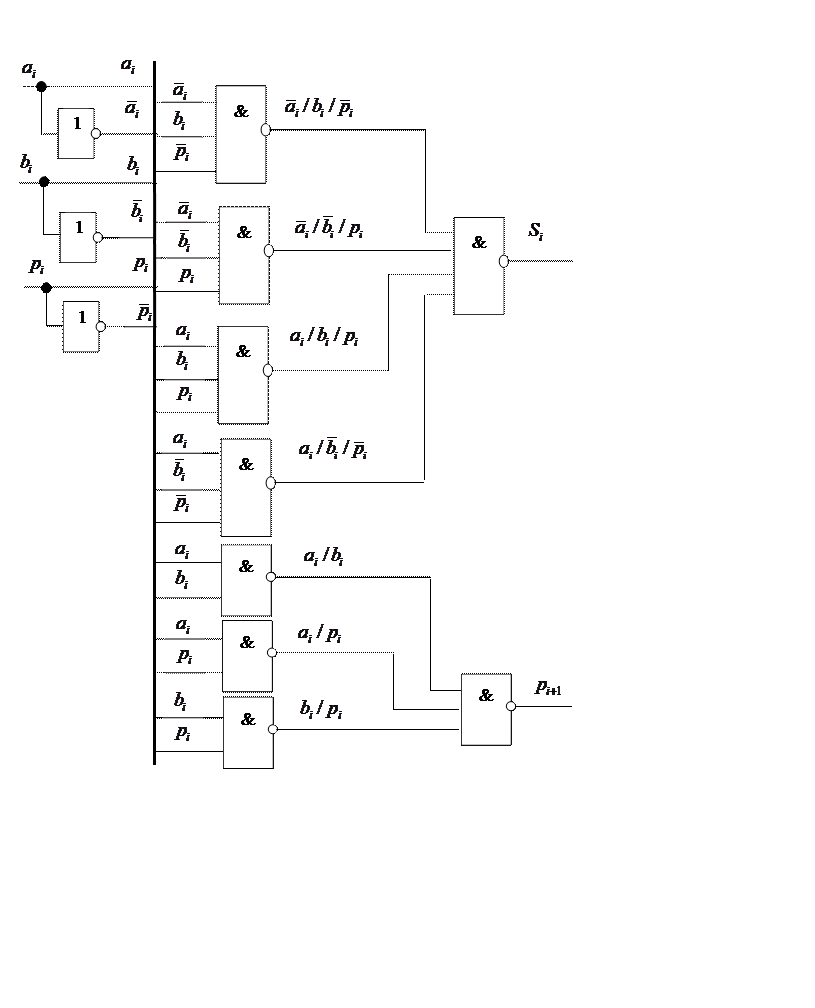
Самостоятельно получите минимальные выражения для этих функций в булевом базисе в дизъюнктивной форме, в булевом базисе в конъюнктивной форме, в базисе Пирса (ИЛИ-НЕ) и начертите схему сумматора в каждом из этих базисов.