Булевы функции. Основные формулы булевой алгебры. Аналитическая запись булевых функций в булевом базисе. Дешифраторы. Мультиплексоры, страница 15

Допустимые претенденты  не покрывают набора 0101 и исключаются. Допустимый претендент  покрывает набор 0101, следовательно, он входит в формулу: . Поскольку матрица единиц после удаления набора 0100 пуста – минимизация закончена.

Получение МКНФ и минимальных форм в базисе Пирса.

В этих базисах допустимые претенденты  ищут,  рассматривая матрицу единиц.  Рассмотрим алгоритм получения МКНФ. Претендентом служит сумма аргументов взятых с отрицанием или без него.

1) Задать длину претендента ;

2) Рассматривая матрицу единиц сформировать очередь всех допустимых претендентов длины ;

3) Если очередь пуста, принять  и перейти к пункту 2, иначе – к пункту 4;

4) Взять первого допустимого претендента из очереди и проверить обнуляет ли он хотя бы один набор в матрице нулей. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5.

5) Включить допустимый претендент в формулу, представляющую собой произведение претендентов;

6) Исключить наборы матрицы нулей, на которых допустимый претендент равен нулю;

7) Исключить претендент из очереди;

8) Если матрица нулей не пуста, то перейти к пункту 3, иначе – конец.

Рассмотрим получение МДНФ той же функции:

,

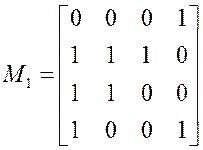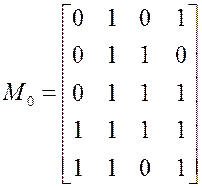
Претенденты  недопустимы, потому что  обращают в нуль хотя бы один набор матрицы единиц.

Из претендентов длины 2 в очередь допустимых претендентов входят . Допустимый претендент  равен нулю на наборах 0101 и 0110 матрицы нулей, поэтому он входит в МКНФ: . После исключения наборов 0101, 0110, 0111 получим:

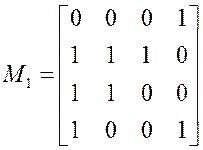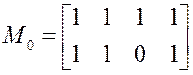,  . Следующий допустимый претендент из очереди  равен нулю на наборах 1111 и 1101 матрицы нулей, т.е. входит в МКНФ: . Т.к. после удаления наборов матрица нулей пуста – минимизация закончена.

Замечание: если искать допустимые претенденты в виде функции Пирса с минимальным числом аргументов, которые равны нулю хотя бы на одном наборе матрицы нулей и равны единице на всех наборах матрицы единиц, то получим минимальную форму в базисе Пирса. Естественно, что следует учитывать особенности этой функции:

- если претендент, равный нулю на наборе матрицы нулей  и равный единице на всех наборах матрицы единиц состоит из одного аргумента, он должен записываться в минимальную форму с дополнительным отрицанием;

- если претендент равен нулю на всех наборах матрицы нулей  и равен единице на всех наборах матрицы единиц, то он записывается с общим отрицанием. Для рассмотренного примера допустимые претенденты, которые входят в минимальную форму: , , а минимальное выражение .

Замечание. При минимизации функций большого числа аргументов, матрицы единиц и нулей занимают значительный объем памяти ЭВМ. При большом числе аргументов его можно уменьшить более чем на порядок, если применить следующий прием: для минимизируемой функции выделяются две матрицы размером , где  - число разрядов в машинном слове;

 - выделенное число слов.

Число слов матрицы при минимизации функции  аргументов определяется по формул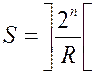е:, где  -символ округления результата к большему целому. Номер набора в матрице определяется его положением:

, где  - номер разряда в слове.

Пример: в гипотетической четырехразрядной машине задана матрица

Разряд    3   2   1  0     

Слово 0    0  0   0  1

Слово 1    0  1   1  0

Слово 2    1  0   0  0

Слово 3    1  0   0  1

Единицы этой матрицы соответствуют наборам 0,5,6,10,11,15.

Минимизируемую функцию задают двумя подобными матрицами.

Исходно эти матрицы заполняются нулями. Затем в матрицу единиц вписывают единицы в позиции, которые соответствуют наборам на которых функция равна единице, а в матрицу нулей вписывают единицы в позиции, которые соответствуют наборам  на которых функция равна нулю.

Пример:

,   .

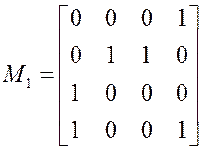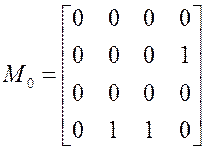Эти матрицы задают не полностью определенную функцию равную единице на наборах 0,5,6,10,11,15 и нулю на наборах 4,13,14.