Булевы функции. Основные формулы булевой алгебры. Аналитическая запись булевых функций в булевом базисе. Дешифраторы. Мультиплексоры, страница 6

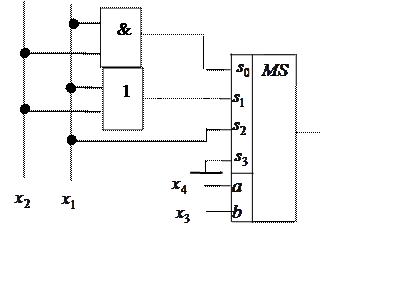
Подключим к адресным входам мультиплексора 4x1 два аргумента, например  и  .  При таком подключении сигнал на адресном  входе  совпадает с , а на входе   с . Поскольку на первых четырех наборах , то сигнал на выходе мультиплексора совпадает с сигналом на шине . Нижняя строчка таблицы на наборах 0, 1, 2, 3 показывает какой сигнал должен формироваться на шине . Эти сигнал не постоянен, следовательно он зависит от еще не учтенных аргументов  и : . Легко увидеть, что логика формирования сигнала .

Рассуждая аналогично можно найти логику формирования сигналов на остальных селектируемых шинах: , , .

Сигнал на      Сигнал на    Сигнал на      Сигнал на

Сложность логики, формирующей сигналы на селектируемых входах, зависит от того, какие аргументы подключены к адресным входам. Оптимальную схему можно получить, выполнив синтез для всех возможных комбинаций адресных сигналов.     

Если брать мультиплексор с числом адресных входов на единицу меньше, чем число аргументов функции, то для реализации функции потребуется мультиплексор и, возможно, один инвертор.

Пример: Реализовать функцию, заданную таблично

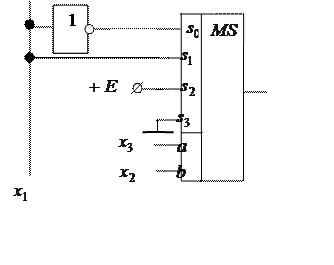Заметим, что если бы на нулевом наборе функция была бы равна нулю, а на первом наборе – равна единице, инвертор не понадобился бы.

Функциональная полнота систем булевых функций.