Математические модели установившегося режима (Лабораторная работа № 3)

Белорусская государственная политехническая академия

            Кафедра электрических станций

Математические задачи энергетики

Лабораторная работа № 3

Математические модели установившегося режима

Автор Бобко Н.Н.

Минск, 2000

Дисциплина " Математические задачи энергетики"

Лабораторная работа №3

Математические модели установившегося режима

1 Цельработы: ознакомление с построением и реализацией математических моделей установившегося режима.

2 Теоретические сведения

Математические модели установившегося режима электроэнергетической системы строятся на основе систем линейных алгебраических уравнений. В этой работе рассматриваются три математические модели установившегося режима:

- обобщенные уравнения состояния электрической цепи на основе первого и второго законов Кирхгофа;

- узловые уравнения;

- контурные уравнения.

2.1. Обобщенныеуравнениясостояниянаосновезаконов Кирхгофа

Обобщенное уравнение состояния электрической цепи на основе законов Кирхгофа имеет вид  [1]:

AI=F;                                                                          (1)

где 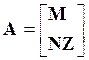       - квадратная матрица m´m, где m - количество ветвей электрической схемы;

M - первая матрица соединений (инциденций), или узловая матрица, размерностью (n-1)´m, где n - количество всех узлов схемы, а (n-1) - количество линейно независимых узлов схемы;

N - вторая матрица соединений (инциденций), или контурная матрица, размерностью k´m, где k - количество линейно независимых контуров схемы;

Z - диоганальная матрица сопротивлений ветвей схемы размерностью m´m;

I - матрица - столбец токов в ветвях схемы размерностью m´1;

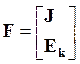 - матрица - столбец правых частей обобщенного уравнения размерностью m´1;

J - матрица - столбец токов источников тока в независимых узлах схемы размерностью (n-1)´1;

Е_к - матрица - столбец контурных электродвижущих сил (ЭДС) в линейно независимых контурах размерностью k´1.

Покажем на примере последовательность построения обобщенного уравнения состояния (1) в развернутой форме для моделирования установившегося режима в схеме замещения электрической системы, приведенной на рис. 1а. Схема имеет пять узлов (n=5), девять ветвей (m=9) и пять линейно независимых контуров: k=m-(n-1)=9-(5-1)=5.

            Для того, чтобы получить систему обобщенных уравнений установившегося режима с ненулевыми диагональными элементами, построим правильный (или нормальный) граф схемы замещения. Раздел графа на подграфы дерева и хорд можно выполнить несколькими вариантами.

В дерево необходимо включить все узлы и столько ветвей, чтобы соединить ими все узлы, но не образовать замкнутых контуров. Базисному узлу присваиваем номер 0, первый узел присоединяем к нулевому ветвью номер 1, второй узел присоединяем к дереву ветвью номер 2, третий узел - ветвью номер 3 и т.д. Все остальные ветви и узлы, которые не вошли в подграф дерева, входят в подграф хорд. Ветви и узлы подграфа хорд произвольно нумеруем возрастающими по порядку цифрами. Произвольно выбираем положительные направления ветвей (рис. 1 б,в). Количество ветвей в дереве определяет количество линейно независимых узлов в схеме замещения, а количество ветвей в подграфе хорд - количество независимых контуров в схеме замещения. Первый контур образовывается ветвью 5, и направление его выбирается совпадающим с направлением ветви 5 (внося ветвь 5 в дерево, получаем первый контур с ветвями 5, 2, 3). Второй контур образовывается ветвью 6 и включает ветви  6, 1, 2 и т.д.

Построим все матрицы, которые входят в уравнение (1).

Первая матрица соединений М показывает, как подключена j-тая ветвь схемы к i-тому узлу: началом (элемент mij матрицы М равный единице), концом (mij=-1) или не подключена совсем (mij=0). Узел с нулевым номером выбираем в качестве базисного, он является линейно зависимым узлом, и для него соответствующая строчка в матрице М не записывается. Номера сопротивлений и источников в схеме соответствуют номерам ветвей. Для схемы на рис.1 матрица М имеет вид:

.

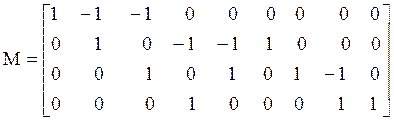Элементы nij матрицы N показывают, входит ли j-ая ветвь схемы в i-ый контур nij=0, когда j-ая ветвь в i-ый контур не входит) и совпадает ли направление j-ой ветви с направлением i-того контура (nіj=1 - совпадает; nіj=-1 - не совпадает):.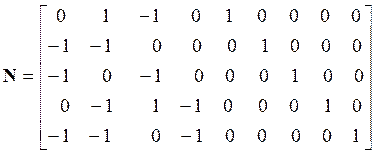

Диоганальная матрица сопротивлений ветвей схемы Z содержит на главной диоганали сопротивления схемы, а ее недиоганальные элементы равны нулю:

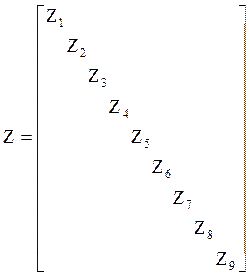
Матрица - столбец неизвестных токов I в ветвях схемы имеет m=9 строк:

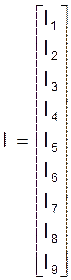
Матрица - столбец токов J источников тока в четырех линейно независимых узлах схемы:

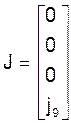
Матрица - столбец контурых ЭДС сил Е_к содержит контурные ЭДС пяти контуров:

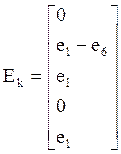
Произведение двух матриц NZ (нижний блок матрицы А в формуле (1)) найдем в соответствии с правилами перемножения двух матриц:

.

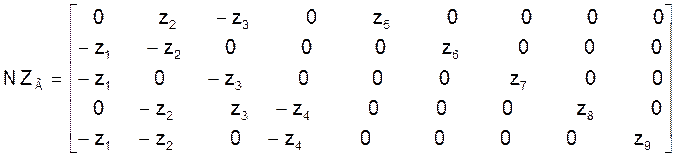Тогда уравнение (1) в развернутой форме для схемы на рис.1 будет иметь вид:

i₁-        i₂                -i₃                                                                                =0;

i₂                                    -i₄             -i₅             +i₆                                                                        =0;