Математические модели установившегося режима (Лабораторная работа № 3), страница 3

Системы уравнений на основе законов Кирхгофа (1), на основе узловых уравнений (3) и на основе контурных уравнений (5) являются тремя основными математическими моделями установившегося режима электрической системы. Порядок систем (3) и (5) значительно ниже, чем порядок системы (1), поэтому математические модели (3) и (5) на практике  применяются значительно чаще, чем модель (1). Токи в ветвях схемы в модели (1) непосредственно определяются как решения системы (1).

Токи в ветвях схемы в модели (3) на основе узловых уравнений при известных узловых напряжениях U_В можно вычислить по следующим формулам, учитывая то, что узловое напряжение u_В0 нулевого узла принято равным нулю:

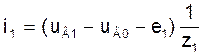
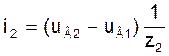
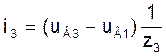
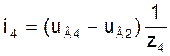
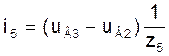
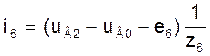                                (7)

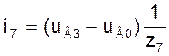
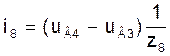
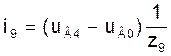
Токи в модели (5) на основе контурных уравнений в ветвях 5, 6, 7, 8, 9, которые являются хордами, есть контурные токи і_к1, і_к2, і_к3, і_к4, і_к5:

і₅=і_к1;              і₆=і_к2;              і₇=і_к3;              і₈=і_к4;              і₉=і_к5.  (8а)

Токи в ветвях 1, 2, 3, 4, которые входят в дерево, можно вычислить по формулам:

і₁=-і_к2-і_к3-і_к5;              і₂=і_к1-i_к2-і_к4-і_к5;

і₃=-і_к1-і_к3+і_к4;              і₄=-і_к4-і_к5.                                            (8б)

2.6 Матэматычныя мадэлi (1), (3), (5) пры наяўнасцi кароткага замыкання (КЗ) у адным з вузлоў схемы

После затухания переходных составляющих наступает установившийся режим короткого замыкания (КЗ), расчет параметров которого является важным для практики и может быть выполнен на основе моделей установившегося режима.

Наличие КЗ в узле 4 схемы на рис.2 изменяет топологические параметры схемы в сравнении с доаварийным режимом (см. схему на рис.1). Количество ветвей остается прежним (m=9). Количество независимых узлов уменьшается на один (n=3), потому что четвертый и нулевой узлы сливаются в один узел. Количество контуров возрастает на один (к=6), потому что перемычка КЗ запирает накоротко ветвь 9 и образовывает новый контур. В точке КЗ схема разделяется на две независимые части: короткозамкнутую ветвь 9 и остальную часть схемы. Система обобщенных уравнений состояния по законам Кирхгофа имеет вид:

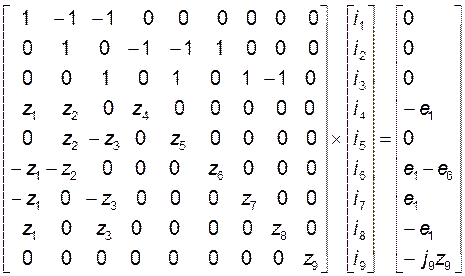.              (9)

В системе (9) создается контур, в котором источник тока j₉ заменен источником ЭДС е₉=j₉z₉.

Узловые уравнения для схемы на рис.2 имеют вид (для узлов 1, 2, 3):

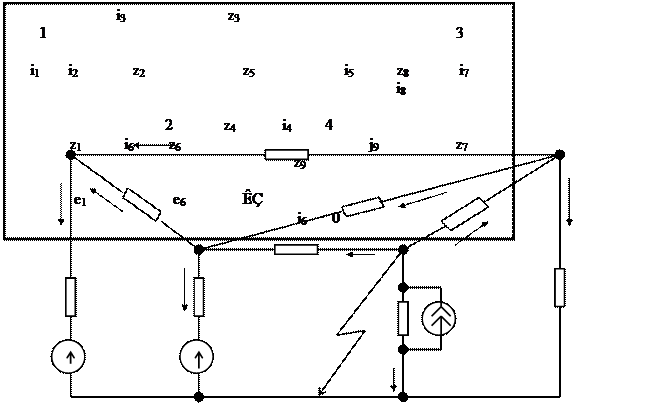
z1=0,1+j0,3;                z2=0,05+j0,4;  z3=0,1+j0,5;                e1=1,1+j0,0; z4=0,08+j0,4;  z5=0,1+j0,4;                z6=0,09+j0,5;  e6=1,3+j0,2; z7=1,5+j0,8;                z8=0,1+j0,5;                z9=0,2+j0,4;                j9=1,0-j2,0. а) схема замещения и ее параметры в относительных единицах;   б) подграф дерева;                                        в) подграф хорд. Рис.2. Схема замещения для аварийного режима работы

.     (10)

Контурные уравнения для схемы на рис.2 записываются для контуров, образовавшихся ветвями 4, 5, 6, 7, 8, 9:

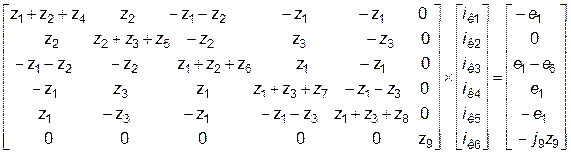(11)

2.7 Численное решение систем (2), (4), (6), (9), (10), (11)

2.7.1 Решение системы (2) обобщенных уравнений состояния для нормального режима работы схемы на рис.1

Система обобщенных уравнений состояния (2) с комплексными значениями коэффициентов и правых частей для нормального режима работы схемы на рис.1 имеет вид

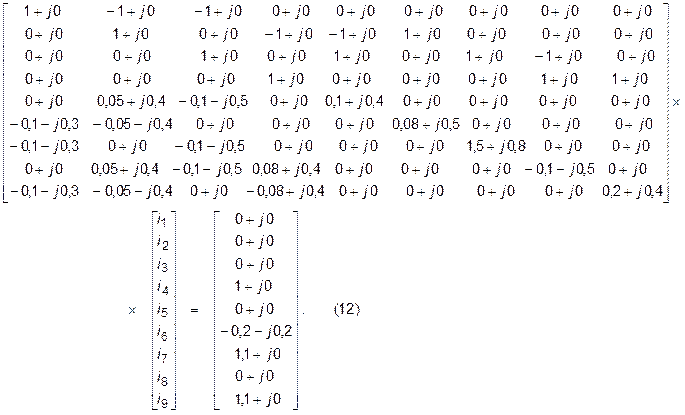
Решение этой системы возможно только точными числовыми методами, потому что условия сходимости итерационного процесса для нее не выполняются. Выполним решение уравнений (12) методом Гаусса (программа GAUSC для решения системы линейных алгебраических уравнений с комплексной матрицей коэффициентов). Файл исходных данных будет иметь вид (kirn.dat):

9

(1.,.)            (-1.,.)           (-1.,.)           (.,.)              (.,.)              (.,.)              (.,.)              (.,.)              (.,.)