Математика \ Математические задачи энергетики

Математические модели установившегося режима (Лабораторная работа № 3), страница 5

і₅=i_к1; і₆=i_к2; і₇=i_к3; і₈=i_к4; і₉=i_к5.

Токи в ветвях 1, 2, 3, 4 получим, применив формулы (8):

i₁=-i_к2-i_к3-i_к5=0,04323-j0,3341-0,5013+j0,3144+0,035+j0,08781=

=-0,06549+j0,06808;

и так далее.

Совпадение токов в ветвях схемы, получившихся в результате решения систем (2), (4), (6), подтверждает правильность формирования и решения трех систем уравнений, которые лежат в основе моделей нормального режима схемы на рис.1.

2.7.4 Решение обобщенных уравнений состояния для режима КЗ в узле 4 схемы на рис .2.

Файл исходных данных для решения системы (9) методом Гаусса имеет вид (файл kirk.dat):

(1.,.) (-1.,.) (-1.,.) (.,.) (.,.) (.,.) (.,.) (.,.) (.,.)

(.,.) (1.,.) (.,.) (-1.,.) (-1.,.) (1.,.) (.,.) (.,.) (.,.)

(.,.) (.,.) (1.,.) (.,.) (1.,.) (.,.) (1.,.) (-1.,.) (.,.)

(.1,.3) (.05,.4) (.,.) (.08,.4) (.,.) (.,.) (.,.) (.,.) (.,.)

(.,.) (.05,.4) (-.1,-.5) (.,.) (.1,.4) (.,.) (.,.) (.,.) (.,.)

(-.1,-.3) (-.05,-.4) (.,.) (.,.) (.,.) (.09,.5) (.,.) (.,.) (.,.)

(-.1,-.3) (.,.) (-.1,-.5) (.,.) (.,.) (.,.) (1.5,.8) (.,.) (.,.)

(.1,.3) (.,.) (.1,.5) (.,.) (.,.) (.,.) (.,.) (.1,.5) (.,.)

(.,.) (.,.) (.,.) (.,.) (.,.) (.,.) (.,.) (.,.) (.2,.4)

(.,.) (.,.) (.,.) (-1.1,.) (.,.) (-.2,-.2) (1.1,.) (-1.1,.) (-1.,.)

Решая систему уравнений (9) с этими исходными данными методом Гаусса, получим токи в ветвях схемы при КЗ в узле 4 (файл kirk.rez):

i₁=-0,2297+j1,0436; i₂=-0,03368+j0,4261;

i₃=-0,1961+j0,6174; i₄=-0,3885+j1,402;

i₅=-0,1957+j0,3416; i₆=-0,5506+j1,3173;

i₇=0,2238-j0,1210; i₈=-0,1659+j0,8380;

i₉=-1,000+j2,000.

2.7.5 Решение системы узловых уравнений (10) для режима КЗ в узле 4 схемы на рис.2.

Файл исходных данных (wuzk.dat) для решения системы (10) методом Жордана (программа JORDC) имеет вид:

(1.6923,-7.385) (-.3077,2.461) (-0.3846,1.9231)

(-.3077,2.4615) (1.7253,-9.1555) (-.5882,2.353)

(-.3846,1.923) (-.5882,2.3529) (1.8765,-6.4759)

(1.1,-3.3) (.84076,-2.44877) (.,.)

В результате решения системы получаем узловые напряжения для узлов 1, 2, 3 (файл wuzk.rez):

u_в1=0,76394+j0,035437; u_в2=0,5918+j0,043272;

u_в3=0,43561-j0,00085.

Токи в ветвях схемы получаем по формулам (7):

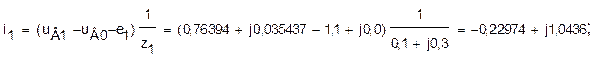
и так далее. Очевидно, что токи в ветвях совпадают с токами, полученными при решении системы (9).

2.7.6 Решение системы контурных уравнений (11) для режима

КЗ в узле 4 схемы на рис.2

Файл исходных данных (konk.dat) для решения системы (11) методом Гаусса (программа GAUSC):

(.23,1.1) (.05,.4) (-.15,-.7) (-.1,-.3) (.1,.3) (.,.)

(.05,.4) (.25,1.3) (-.05,-.4) (.1,.5) (-.1,-.5) (.,.)

(-.15,-.7) (-.05,-.4) (.24,1.2) (.1,.3) (-.1,-.3) (.,.)

(-.1,-.3) (.1,.5) (.1,.3) (1.7,1.6) (-.2,-.8) (.,.)

(.1,.3) (-.1,-.5) (-.1,-.3) (-.2,-.8) (.3,1.3) (.,.)

(.,.) (.,.) (.,.) (.,.) (.,.) (.2,.4)

1 2 3 4 5 6

Скачать файл