Математические модели установившегося режима (Лабораторная работа № 3), страница 2

i₃                                    +i₅                                +i₇            -i₈                                 =0;

i₄                                                                            +i₈            +i₉            =j_9;

i₂z₂          -i₃z₃                            +i₅z₅                                                                                       =0;                   (2)

-i₁z₁        -i₂z₂                                                                    +i₆z₆                                                                   =e₁-e₆;

-i₁z₁                            -i₃z₃                                                                    +i₇z₇                                               =e_1;

-i₂z₂        +i₃z₃       -i₄z₄                                                                    +i₈z₈                           =0;

-i₁z₁        -i₂z₂                            -i₄z₄                                                                                        +i₉z₉       =e₁;

Первые четыре уравнения системы (2) - это уравнения первого закона Кирхгофа для узлов 1, 2, 3, 4, а последние пять - это уравнения второго закона Кирхгофа для контуров 1, 2, 3, 4, 5. При этом ток источника тока j9 вошел в матрицу J (правая часть узловых уравнений), а ЭДС е1 и е6 - в матрицу Ек (правая часть контурных уравнений).

2.2 Узловые уравнения

Узловые уравнения связывают неизвестные узловые напряжения с заданными параметрами схемы и заданными параметрами режима схемы. Система узловых уравнений в матричной форме имеет вид [1,2]:

Y_вU_в=J-MY_вЕ.

Если все источники электрической схемы представить в виде источников тока (матрица ЭДС ветвей схемы Е=0), то система уравнений для узловых напряжений упрощается:

Y_вU_в=J                                                                        (3), где       Y_в - матрица узловых проводимостей схемы размерностью (n-1)´(n-1) (n-количество узлов схемы); элемент yii матрицы Yв, который находиться в i-ой строчке на главной диагонали, равный сумме проводимостей ветвей, подключенных к i-ому узлу схемы (собственная проводимость i-ого узла); элемент yij на пересечении i-той строчки и j-ого столбца матрицы Yв равный взятой с знаком минус проводимости ветви, включенной между i-ым и j-ым узлами схемы (взаимная проводимость между i-ым и j-ым узлами);

;

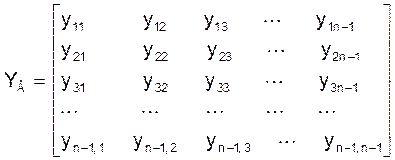U_в - матрица – столбец размерностью  (n-1)´(n-1) низвестных узловых напряжений в линейно независимых узлах схемы:

;

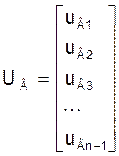J - матрица - столбец размерностью (n-1)´1 токов источников тока, которые действуют в независимых узлах схемы (положительное направление токов - от узла):

.

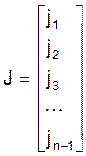Система узловых уравнений (3) для схемы на рис.1 будет иметь вид:

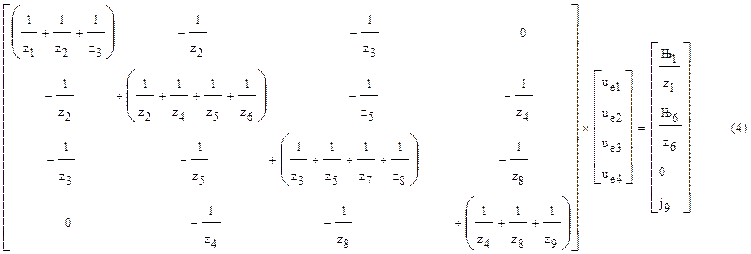                    В этой системе, в соответствии с принятой моделью (3), ЭДС в ветвях 1 и 6 заменены источниками тока j₁ и j₆:

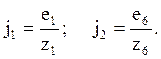
2.4 Контурные уравнения

Контурные уравнения в матричной форме имеют вид [1,2]:

.

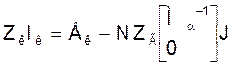Для схемы, в которой все источники электрической энергии представлены источниками ЭДС (матрица токов источников тока J=0), эти уравнения упрощаются:

Z_кI_к=Е_к                                                                       (5)

где:     Z_к - матрица контурных сопротивлений:

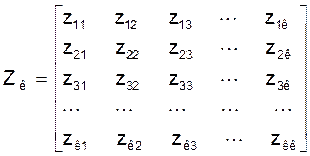, которая имеет порядок к (количество линейно независимых контуров схемы). Диагональный элемент zii этой матрицы равен сумме сопротивлений ветвей, которые входят в i-тый контур. Недиагональный элемент zij равен сумме сопротивлений ветвей, которые входят одновременно в i-тый и в j-тый контуры, причем сумма имеет знак плюс, когда направления i-того и j-того контуров в этих ветвях совпадают, и знак минус,. когда не совпадают.

I_к - матрица - столбец низвестных контурных токов размерностью к´1:

;

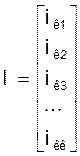Z_к - матрица - столбец заданных контурных ЭДС размерностью к´1:

.

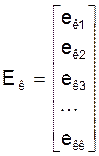Для схемы на рис.1а система контурных уравнений (5) в развернутой форме имеет вид:

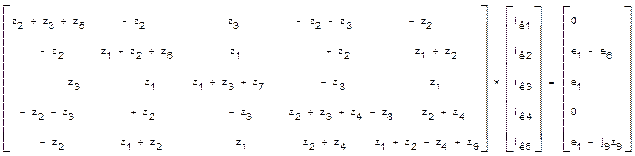     (6)

Порядок этой системы определяется количеством линейно независимых контуров схемы (к=5). В этой системе, в соответствии с принятой моделью (5), источник тока j9 в ветви 9 заменен источником ЭДС е9=j9z9.

2.5 Расчет токов в ветвях схемы при использовании моделей на основе узловых и контурных уравнений