Разлік рэжымаў электрасістэмы лікававымі метадамі

першая матрыца спалучэнняў (інцыдэнцый), або ўзлавая матрыца, памерам (n-1)´m, дзе n – колькасць усіх вузлоў схемы, а (n-1) - колькасць лінейна незалежных узлоў схемы;

N – другая матрыца спалучэнняў (інцыдэнцый), ці контурная матрыца, памерам k´m, дзе k колькасць лінейна незалежных кантуроў схемы; 

Z_д - дыяганальная матрыца супраціўленняў галін схемы памерам m´m;

I- матрыца-слупок токаў у галінах схемы памерам m´1;

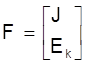-матрыца-слупок правых частак абагульненнага раўнання памерам m´1; 

J - матрыца-слупок крыніц токаў тока ў незалежных вузлах схемы памерам (n-1)´1; 

Е_к - матрыца-слупок контурных ЭРС у лінейна незалежных контурах памерам k´1.

Для нашай схемы матрыцы Aі Fбудуць мець наступны выгляд:

табліца 4.1 Матрыцы А і F

1	-1	0	0	0	0	0	0	0	0	0	-1	0	-1	0
0	1	-1	0	0	0	1	0	0	0	0	0	-1	0	0
0	0	1	-1	0	0	0	1	0	0	0	0	0	0	0
0	0	0	1	-1	0	0	0	1	0	0	0	0	0	0
0	0	0	0	1	-1	0	0	0	1	0	1	0	0	0
0	0	0	0	0	1	0	0	0	0	1	0	1	1	0
		0	0	0	0		0	0	0	0	0	0	0
			0	0	0	0		0	0	0	0	0	0
				0	0	0	0		0	0	0	0	0
					0	0	0	0		0	0	0	0
						0	0	0	0		0	0	0
0					0	0	0	0	0	0		0	0	0
0	0					0	0	0	0	0	0		0	0
0						0	0	0	0	0	0	0		0

табліца 4.2 Лікавыя значэнні матрыцы A

1	-1	0	0	0	0	0	0	0	0	0	-1	0	-1	0
0	1	-1	0	0	0	1	0	0	0	0	0	-1	0	0
0	0	1	-1	0	0	0	1	0	0	0	0	0	0	0
0	0	0	1	-1	0	0	0	1	0	0	0	0	0	0
0	0	0	0	1	-1	0	0	0	1	0	1	0	0	0
0	0	0	0	0	1	0	0	0	0	1	0	1	1	0
-8.307	-1.134	0	0	0	0	1.6	0	0	0	0	0	0	0	-0.412
-8.307	-1.134	-0.907	0	0	0	0	34.475	0	0	0	0	0	0	-1.375
-8.307	-1.134	-0.907	-0.832	0	0	0	0	5.238	0	0	0	0	0	-0.734
-8.307	-1.134	-0.907	-0.832	-0.681	0	0	0	0	2.753	0	0	0	0	-0.545
-8.307	-1.134	-0.907	-0.832	-0.681	-1.059	0	0	0	0	5.378	0	0	0	-0.608
0	-1.134	-0.907	-0.832	-0.681	0	0	0	0	0	0	0.756	0	0	0
0	0	-0.907	-0.832	-0.681	-1.059	0	0	0	0	0	0	1.059	0	0
0	-1.134	-0.907	-0.832	-0.681	-1.059	0	0	0	0	0	0	0	0.605	0

Праводзячы разлік лікавым метадам Жардана, атрымоўваем наступны вынік:

  

  

  

  

   

    

Базісны ток,  кА:  

Разлічым токі ў іменаваных адзінках, кА:

5.  Разлік токаў трохфазнага кароткага замнення на аснове                            раўнанняў па законах Кірхгофа і лікавага метада Жардана

Фарміруем матрыцы F і A :

табліца 5.1 Матрыцы A і F

1	0	0	0	0	-1	0	0	0	0	0	-1	-1	0	0
0	1	0	0	0	1	-1	0	0	0	-1	0	0	0	0
0	0	1	0	0	0	1	-1	0	0	0	0	0	0	0
0	0	0	1	0	0	0	1	-1	0	0	0	0	0	0
0	0	0	0	1	0	0	0	0	1	1	0	1	0	0
		0	0	0		0	0	0	0	0	0	0	0
0			0	0	0		0	0	0	0	0	0	0
0	0			0	0	0		0	0	0	0	0	0
0	0	0		0	0	0	0		0	0	0	0	0
0	0	0	0		0	0	0	0		0	0	0	0
0		0	0		0	0	0	0	0		0	0	0
	0	0	0	0	0	0	0	0	0	0		0	0
	0	0	0		0	0	0	0	0	0	0		0
0	0	0	0	0	0	0	0	0	0	0	0	0

табліца 5.2 Лікавыя значэнні матрыцы A і F

1	0	0	0	0	-1	0	0	0	0	0	-1	-1	0	0
0	1	0	0	0	1	-1	0	0	0	-1	0	0	0	0
0	0	1	0	0	0	1	-1	0	0	0	0	0	0	0
0	0	0	1	0	0	0	1	1	0	0	0	0	0	0
0	0	0	0	1	0	0	0	0	1	1	0	1	0	0
1.659	-0.246	0	0	0	1.134	0	0	0	0	0	0	0	0	0.002
0	0.246	-3.288	0	0	0	0.907	0	0	0	0	0	0	0	-0.002
0	0	3.288	-0.751	0	0	0	0.832	0	0	0	0	0	0	0.015
0	0	0	-0.751	0	0	0	0	0.681	0	0	0	0	0	1.114
0	0	0	0	-0.805	0	0	0	0	1.059	0	0	0	0	1.113
0	0.246	0	0	-0.805	0	0	0	0	0	1.059	0	0	0	0.012
1.659	0	0	0	0	0	0	0	0	0	0	0.756	0	0	-1.099
1.659	0	0	0	-0.805	0	0	0	0	0	0	0	0.605	0	0.014
0	0	0	0	0	0	0	0	0	0	0	0	0	0.415	1.112

Праводзячы разлік лікавым метадам Жардана, атрымоўваем наступны вынік:

  

  

  

 

 

Базісны ток,  кА:  

Разлічым токі ў іменаваных адзінках, кА:

Ток   кароткага замкнення:

6.  Разлік токаў кароткага замкнення з выкарыстоўваннем праграмы TKZ

В Ы Х А Д Н Ы   Ф А Й Л   П Р А Г Р А М Ы   TKZ

УВАХОДНЫЯ ДАДЗЕНЫЯ:

Прызнак разлiку каэфiцыентау размеркавання токау КЗ

па галiнах схемы NRKRTKZH=2

Прызнак схемы нулявой паслядоунасцi NSNP=0

Колькасць галiн у схеме прамой паслядоунасцi KH=14

Колькасць вузлоу кароткага замыкання KWKZ= 1

Колькасць галiн у схеме нулявой паслядоунасцi KHSNP= 0

Колькасць вузлоу у схеме нулявой паслядоунасцi, якiя маюць нулявы патэнцыял KWSNPNP= 0

Базiсная магутнасць SB= 1000. MVA

Iнфармацыя аб галiнах схемы прамой паслядоунасцi:

N1K(KH) N2K(KH)    X(KH)      SNG(KH)

адн.адз.      МВА

0      1     1.6590        157.

0      2      .2460       1125.

0      3     3.2880         80.

0      4      .7510        412.

0      6      .8050        375.

1      2     1.1340          0.

2      3      .9070          0.

3      4      .8320          0.

4      5      .6810          0.

5      6     1.0590          0.

2      6     1.0590          0.

1      5      .7560          0.

1      6      .6050          0.

0      5      .4150        705.

Iнфармацыя аб вузлах кароткага замыкання:

NWKZ(KWKZ)   UB(KWKZ)

кВ

5        230.0

РЭЗУЛЬТАТЫ РАЗЛIКУ:

НУМАР ВУЗЛА  КЗ:    5

Базiснае напружанне вузла КЗ, кВ:     230.000000

Базiсны ток у вузле КЗ, кА:       2.510219

Рэзультатыунае супрац. схемы адносна вузла КЗ:

-для токау прамой (адв.) паслядоун. (адн.адз.)    2.226158E-01

Перыядычная састаул. звышпераходн. току КЗ (КА):

- трохфазнае      11.276010

- двухфазнае       9.765312

Сiметрычныя састауляльныя току КЗ (КА):

Прамая      Адваротная  Нулявая

- трохфазнае     11.2760

- двухфазнае      5.6380      5.6380

Каэфiцыенты размеркавання сiметрычныых састауляльных тока КЗ па галiнах схемы (дадатным накiрункам у галiне лiчыцца накiрунак ад канца галiны з большым нумарам да канца з меньшым нумарам)

Галiна схемы      Прамая   Адваротная     Нулявая

0    1      -.0634       .0634

0    2      -.1406       .1406

0    3      -.0184       .0184

0    4      -.1330       .1330

0    6      -.1082       .1082

1    2       .0622      -.0622

2    3      -.0287       .0287

3    4      -.0472       .0472

4    5      -.1802       .1802

5    6       .1280      -.1280

2    6      -.0496       .0496

1    5      -.1554       .1554

1    6       .0298      -.0298

0    5      -.5364       .5364

Галіны у спісе пералічаны у парадку , які адпавядае нумарацыі галін пры разліку рэжыму кароткага замкнення у раздзелах 3 і 5

Токі ў іменаваных адзінках,  кА:

Вынік атрымаўся з дакладнасцю прыблізна 10% у параўнанні з разлічанымі токамі по метаду Жардана. Гэта абумоўлена тым , што супрациуленне генератарау мы прыняли за 1 .

Токі ў галінах 9 і 12 (мал. 3.1 ) атрымаліся з адваротным знакам , таму што пры перабудове схемы з мал 1.2 да мал 3.1 для гэтых галін былі выбраны адваротныя напрамкі .

7.  Разлік пераходнага рэжыму

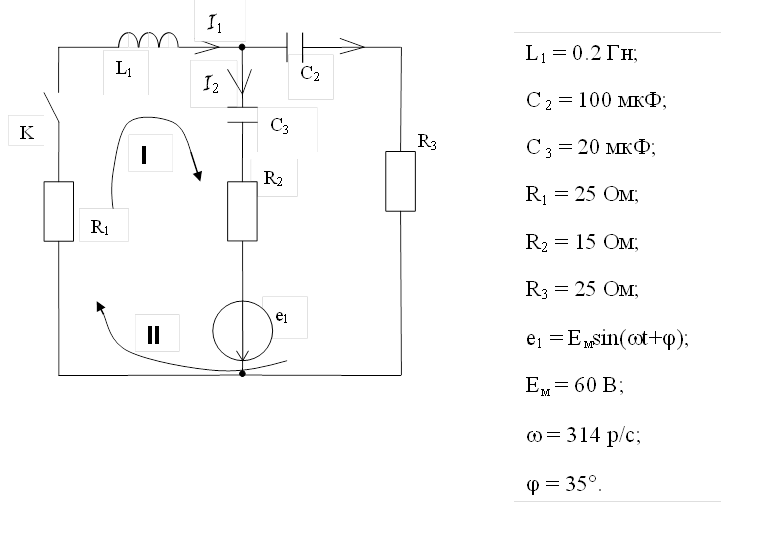  Патрэбна разлічыць лікавым метадам токі ў галінах схемы і напружанні на элементах схемы ў пераходным рэжыме, які ўзнікае пасля замыкання ключа.

мал 7.1 Схема замяшчэння энергасістэмы для разліку пераходнага рэжыму

Пасля замкнення ключа  ў схеме атрымоўваецца два лінейна незалежных контура і адзін лінейна незалежны вузел. Саставім сістэму раўнанняў па законах Кіргофа:

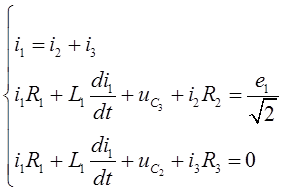(1)

Гэтая сістыма не з’яўляецца замкненай, пагэтаму неабходна дапоўніць яе яшчэ двума раўнаннямі.

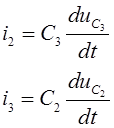
Атрымоўваем сістэму наступнага выгляду:

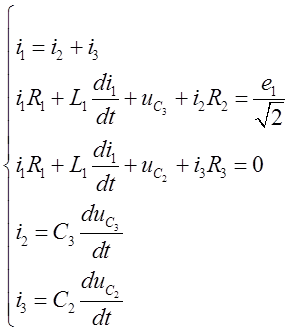                               (2)

Выразім ток з першага раўнання і падставім у астатнія.

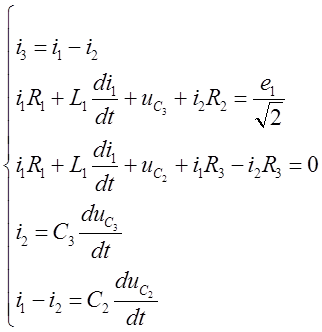
Падставім выраз для  (4-ае раўнанне) ва ўсе астатнія раўнанні.

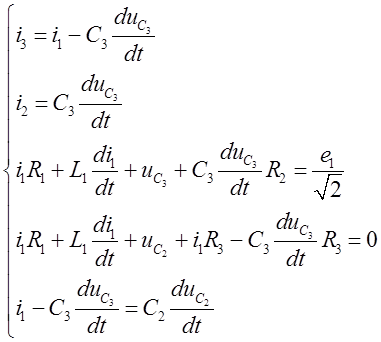
Праз суму 3 і 4 раўнання пасля дзялення кожнага  адпаведна на

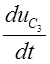 і   атрымоўваем выраз для . Праз рознасць 3 і 4 раўнання атрымоўваем выраз для і адразу ж падстаўляем яго у 5 раўнанне і атрымоўваем выраз для .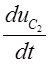

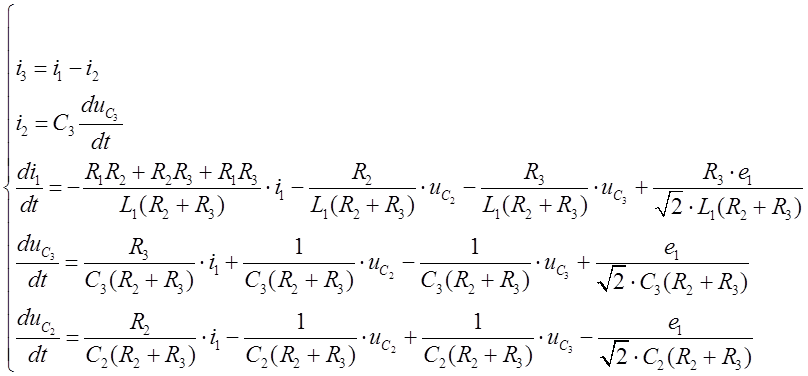
Сістэма дыферэнцыяльных раўнанняў (2), зведзеная да нармальнага стану,  з выключанымі невядомымі і  наступная:

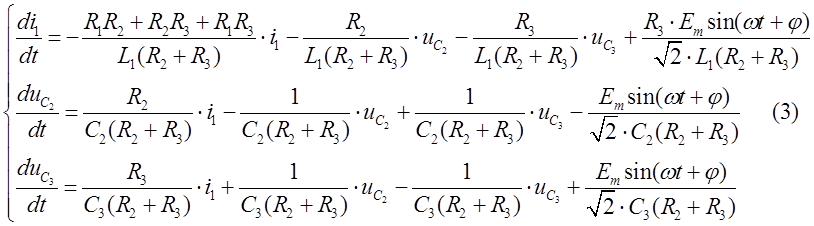
Атрыманая такім чынам сістэма раўнанняў (3), якая з’яўляецца сістэмай дыферэнцыяльных раўнанняў у нармальнай форме, прыдатная да лікавага рашэння пры дапамозе стандартных падпраграм.

Разлічым пачатковыя ўмовы. Разлік будзем весці ў дзейных значэннях велічынь. Да замкнення ключа ў схеме меўся адзін контур, такім чынам:

;

;

;

;

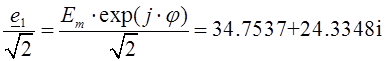
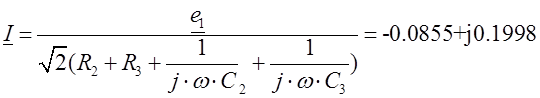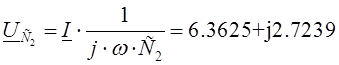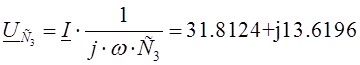
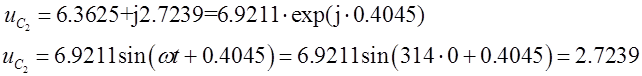
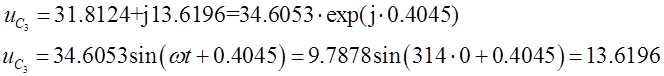
Такім чынам пачатковыя ўмовы наступныя:

                    

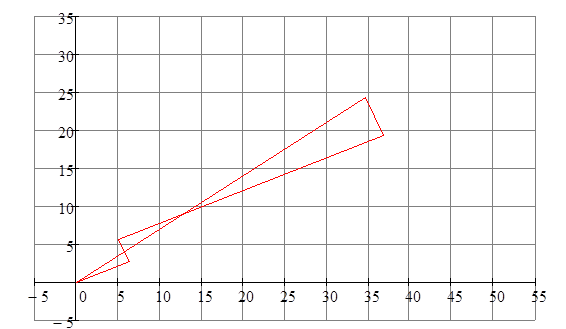
Па выніках разліку пабудуем вектарную дыяграму напружанняў для ўсталяванага дааварыйнага рэжыму

мал 7.2 Вектарная дыяграма напружанняў для ўсталяванага дааварыйнага рэжыму

Ведаючы пачатковыя ўмовы, разлічым сістэму дыферэнцыяльных