Метады рашэння сістэм лінейных алгебраічных раўнанняў (Лабараторная работа № 2)

Міністэрства адукацыі Рэспублікі Беларусь

Беларуская дзяржаўная політэхнічная акадэмія

Кафедра электрычных станцый

Матэматычныя задачы энергетыкі

Лабараторная работа №2

Метады рашэння сістэм

 лінейных алгебраічных  раўнанняў

Аўтар Бобка М.М.

Мінск, 2000

Міністэрства адукацыі Рэспублікі Беларусь

Беларуская дзяржаўная політэхнічная акадэмія

Кафедра электрычных станцый

Дысцыпліна: Матэматычныя задачы энергетыкі

Лабараторная работа №2

Метады рашэння сістэм лінейных алгебраічных раўнанняў

1.   Мэта работы

Мэтай работы з¢яўляецца вывучэнне алгарытмаў i прграм для рашэння сiстэм лiнейных алгебраiчых раўнанняў (СЛАУ) i набыцце навыкаў выкарыстання гэтых метадаў.

2.   Кароткiя тэартычныя звесткi

2.1. Метады рашэння сiстэм лiнейных алгебраiчных раўнанняў (СЛАУ)

Для даследавання ўсталяванага рэжыму электрнычных сiстэм прымяняюцца матэматычныя мадэлi на аснове алгебраiчных раўнанняў. Для разлiку параметраў ўсталяванага рэжыму патрабуецца рашыць сiстэму алгебраiчных раўнанняў якiм-небудзь лiкавым метадам. Вядомы два асноўных метады рашэння такiх сiстэм: дакладныя i iтэрацыйныя. Дакладныя метады дазваляюць разлiчыць каранi сiстэмы пасля выканання папярэдне вядомай колькасцi арыфметычных аперацый (формулы Крамера, метад Гаўса, метад галоўных элементаў, схема Жардана, метад квадратных каранёў i iнш.). Пры выкарыстанні ітэрацыйных метадаў развязанне знаходзіцца шляхам паслядоўных набліжэнняў.

Для дакладных метадаў характэрна вылiчальная хiбнасць, абумоўленая акругленнем пры вылiчэннях. Iтэрацыйныя метады, акрамя вылiчальнай хiбнасцi, валодаюць таксама метадычнай хiбнасцю (хiбнасцю метада). Каэфіцыенты сістэмы павінны задавальняць ўмовам збежнасці пры выкарыстанні ітэрацыйных метадаў; г. зн., не ўсякую СЛАУ можна развязаць ітэрацыйнымі метадамі. Аднак iтэрацыйныя метады з'яўляюцца адзінымі метадамі рашэння нелiнейных алгебраiчных раўнанняў. Ітэрацыйныя метады таксама валодаюць уласцiвасцю самавыпраўляльнасцi: памылкi i збоi ў вылiчальным працэсе могуць быць ўспрыняты як новае наблiжэнне.

2.2. Дакладныя метады

2.2.1. Метад Гаўса

Метад Гаўса, або метад паслядоўнага выключэння невядомых велiчынь, або схема адзiнага дзялення, з¢яўляецца найбольш распаўсюджаным метадам рашэння СЛАУ. У матрычнай форме СЛАУ мае выгляд:

АХ=В,                                                                                                 (1)

дзе      А -- квадратная n´n матрыца лiкавых каэфiцыентаў пры невядомых велiчынях (n – парадак СЛАУ);

Х – матрыца-слупок n невядомых велiчынь, або матрыца развязанняў СЛАУ;

В – матрыца-слупок n правых частак СЛАУ.

У разгорнутай форме пры n=3 сiстэма мае выгляд:

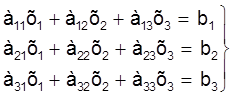                                                              (2)

дзе:

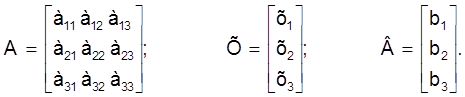
Няхай каэфiцыенты а₁₁, а₂₂, а₃₃ на галоўнай дыяганалi не роўны нулю (у адваротным выпадку пераставiм раўнаннi ў сiстэме (2) так, каб на галоўнай дыяганалi не было нулявых каэфiцыентаў). Выканаем выключэнне невядомай велiчынi х₁ з сiстэмы (2). Для гэтага раздзелiм першае раўнанне сiстэмы (2) на каэфiцыент а₁₁ пры невядомай велiчынi х₁:

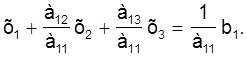                                                           (3)

Памножым цяпер раўнанне (3) на каэфiцыент а₂₁ (пры невядомай х₁ у другiм раўнаннi сiстэмы (2))

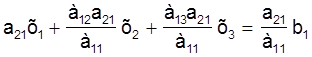
i адымем гэтае раўнанне ад другога раўнання сiстэмы (2):

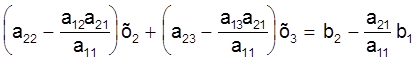                          (4)

Таксама памножым раўнанне (3) на каэфіцыент а₃₁ (пры невядомай х₁ у трэцім раўнанні сістэмы (2))

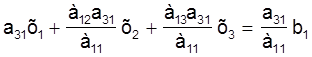
і адымем гэтае раўнанне ад трэцяга раўнання сістэмы (2):

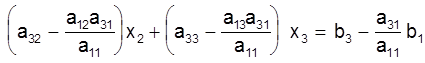                        (5)

Раўнаннi (4) i (5) утвараюць новую сiстэму, з якой выключана невядомая х₁, а парадак гэтай сiстэмы на адзiнку меньшы парадку сiстэмы (3). Гэты алгарытм называецца алгарытмам паслядоўнага выключэння i можа быць прыменены да сiстэмы любога парадку. Вызначыўшы невядомыя велiчынi х₂ і х₃ з раўнанняў (4) i (5), можна падставiць iх у раўнанне (3) i знайсцi з яго велiчыню х₁.

Увядзем новыя абазначэннi каэфiцыентаў i свабодных членаў у раўнаннях (3)-(5):

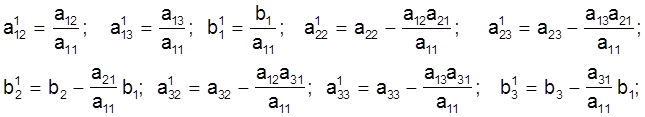
i запiшам сiстэму (2) у наступным выглядзе:

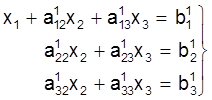                                                                  (6)

Выключаючы аналагічна невядомую велічыню х₂ з трэцяга раўнання сiстэмы (6) i ўводзячы новыя абазначэннi каэфіцыентаў

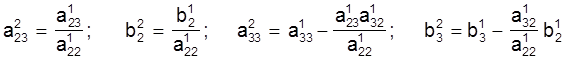, пераўтворым сiстэму (6) да выгляду:

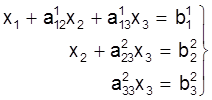                                                                  (7)

З трэцяга раўнання сiстэмы (7) можна вызначыць х₃:

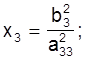                                                                                            (8)

з другога:                                                            (9)

і з першага                                                   (10)

Працэс паслядоўных пераходаў ад сiстэмы (2) до сiстэм (6) i (7) называецца прамым ходам метаду Гаўса (трыангуляцыя матрыцы каэфiцыентаў), а вылiчэнне невядомых велiчынь х₃, х₂, х₁ па па формулах (8)-(10) – зваротным ходам метаду Гаўса.

Прыклад 1. Рашыць метадам Гаўса СЛАУ: