Метады рашэння сістэм лінейных алгебраічных раўнанняў (Лабараторная работа № 2), страница 2

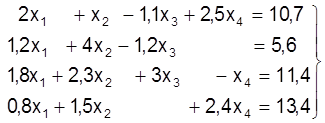
Выключаем невядомую x₁ з другога, трэцяга i чацвёртага раўнанняў. Для гэтага дзелiм першае раўнанне на каэфiцыент а₁₁=2. Затым памнажаем гэтае раўнанне адпаведна на а₂₁=1,2; а₃₁=1,8; а₄₁=0,8 i адымаем яго паслядоўна ад другога, трэцяга i чацвертага раўнанняў:

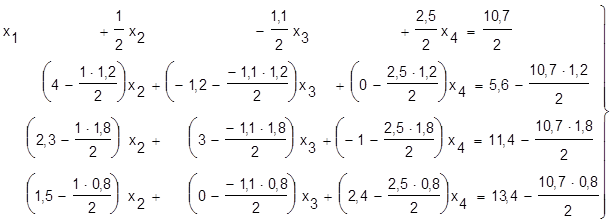, або пасля выканання арыфметычных аперацый:

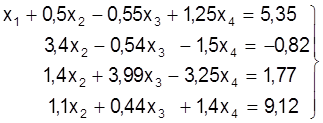                                            (11)

Цяпер прыменiм апiсаны вышэй алгарытм для выключэння невядомай пераменнай х₂ з трэцяга i чацвёртага раўнанняў сiстэмы (11), пасля чаго яна прыме выгляд:

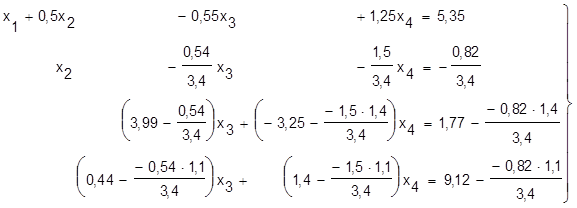, або:

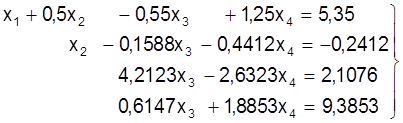.                           (12)

Выключым невядомую велiчыню х₃ з чацвёртага раўнання сiстэмы (12):

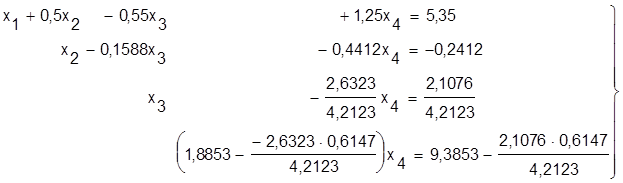, або:

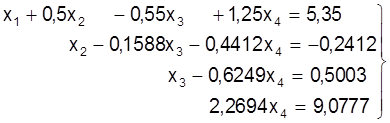
З апошняга раўнання можна вызначыць х₄=9,0777/2,2694=4,0. На гэтым прамы ход метада Гаўса закончаны. Квадратная матрыца каэфiцыентаў пераўтварана ў верхнюю трохвугольную. Сiстэма мае выгляд:

.

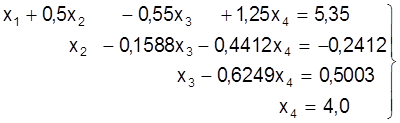Цяпер можна выканаць зваротны ход метада Гаўса i вызначыць невядомыя велiчынi:

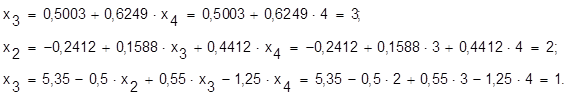
Такiм чынам, маем рашэнне ў выглядзе:

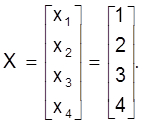
2.2.2. Схема Жардана

Гэтая схема з¢яўляецца мадыфiкацыяй метаду Гаўса i заключаецца ў тым, што выключэнне кожнай невядомай велiчынi выконваецца не толькi для тых раўнанняў, якiя знаходзяцца нiжэй бягучага раўнанання  ў сiстэме, а для ўсiх раўнанняў сiстэмы. У вынiку гэтага матрыца А каэфiцыентаў пры невядомых пераўтвараецца ў адзiнкавую матрыцу, а на месцы правых частак знаходзяцца невядомыя велiчынi Х. Схема Жардана мае толькi прамы ход.

Прыклад 2. Рашыць СЛАУ па схеме Жардана:

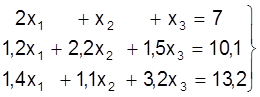                                                         (13)

Выключаем невядомую велiчыню х₁ з другога i трэцяга раўнанняў сiстэмы (13). Дзелiм першае раўнанне на каэфiцыент а₁₁=2. Памнажаем гэтае раўнанне на а₂₁=1,2 i адымаем яго ад другога раўнання, а таксама памнажаем яго на а₃₁=1,4 i адымаем ад трэцяга раўнання:

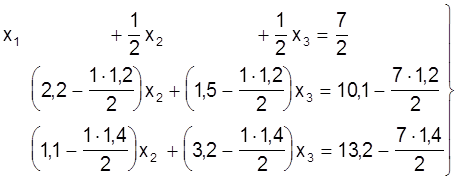, або:

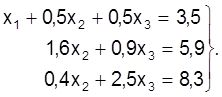
Невядомая пераменная х₁ з другога i трцяга раўнання выключана. Да гэтага моменту адрозненняў ад метаду Гаўса няма. Выключым цяпер невядомую х₂ з першага i трэцяга раўнанняў. Для гэтага раздзелiм другое раўнанне на каэфiцыент. Памножым гэтае раўнанне на каэфiцыент  i адымем яго ад першага раўнання. Памножым яго таксама на каэфiцыент  i адымем ад трэцяга раўнання:

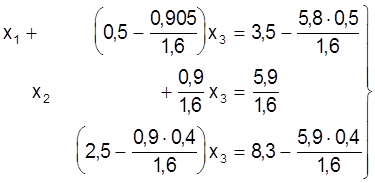, або:

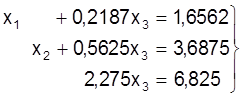
Аналагiчна выключаем пераменую х₃ з першага i другога раўнанняў:

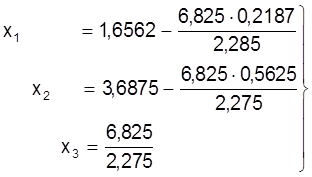, або:

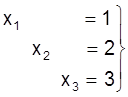
што з¢яўляецца рашэннем сiстэмы (1).

2.2.3. Абарачэнне квадратнай матрыцы метадам Гаўса

Для неасаблiвай матрыцы iснуе асноўнае судачынене:

                                                                                       (14)

дзе:     A^-1 – матрыца, адваротная матрыцы A;

E – адзiнкавая матрыца.

Разгледзiм алгарытм абарачэння для матрыцы A трэцяга парадку:

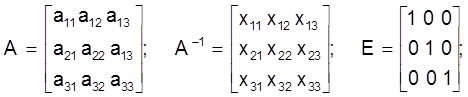
Перамнажаючы матрыцы A i A^-1, будзем мець n сiстэм раўнанняў адносна n´n невядомых элементаў x_ij матрыцы A^-1;

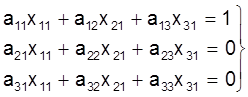;                                                          (15)

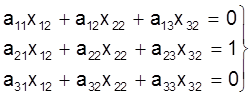;                                                         (16)

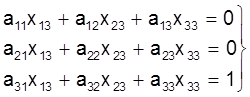.                                                          (17)

Невядомымi велiчынямi ў сiстэмах (15), (16), (17) з¢яўляюцца слупкi матрыцы A^-1. Сiстэмы (15)-(17) маюць адну i тую ж матрыцу каэфiцыентаў A, але розныя правыя часткi, таму iх можна рашаць як адну сiстэму з некалькiмi правымi часткамi.

Прыклад. Выкарыстоўваючы метад Гаўса, знайсцi матрыцу, адваротную матрыцы А:

.

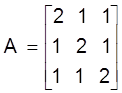Састаўляем пашыраную матрыцу [AE], якая складаецца з двух блокаў ( з матрыц A i E):

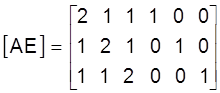
Прымяняем да пашыранай матрыцы аднаходавы алгарытм Гаўса (схему Жардана). Пасля выключэння невядомых x_1j (j=1, 2, 3) з другога i трэцяга раўнанняў сiстэм (15)-(17) пашыраная матрыца будзе мець выгляд:

.

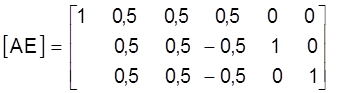Пасля выключэння невядомых x_2j (j=1, 2, 3) з першага і трэцяга, а затым х_3j (j=1, 2, 3) з першага і другога раўананяў  сістэм (15)-(17) пашыраная матрыца будзе мець выгляд:

[AE]=.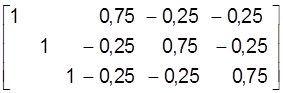

На месцы матрыцы A мы атрымалi адзiнкавую матрыцу трэцяга парадку, а на месцы адзiнкавай матрыцы E – матрыцу А^-1, адваротную матрыцы A. Такiм чынам, адваротная матрыца мае выглдя:

A^-1=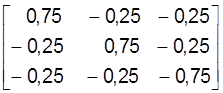

Для праверкi правiльнасцi падставiм матрыцу A^-1 у формулу (14) i выканаем перамнажэнне матрыц.

2.3. Iтэрацыйныя (наблiжаныя) метады рашэння СЛАУ

2.3.1. Метад простай iтэрацыi