Метады рашэння сістэм лінейных алгебраічных раўнанняў (Лабараторная работа № 2), страница 3

Сiстэма алгебраiчных раўнанняў (2) для рашэння яе метадам простай iтэрацыi спачатку пераўтвараецца да выгляду, зручнаму для правядзення iтэрацый. Для гэтага кожнае раўнанне вырашаецца адносна невядомых пераменных x₁, x₂, x₃, якiя знаходзяцца на галоўнай дыяганалi ў сiстэме (2) (папярэдне раўнанні ў сістэме (2) перастаўляюцца так, каб на галоўнай дыяганалі каэфіцыенты былі па модулю найбольшымі сярод астатніх каэфіцыентаў радка):

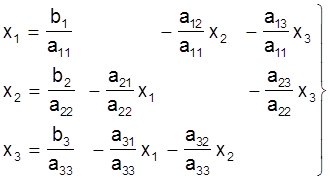                                           (18)

Уводзячы матрыцы

C=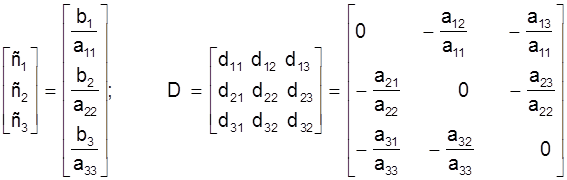, сiстэму (18) можна запiсаць у выглядзе:

X=C+DX.                                                                                            (19)

Невядомая велiчыня X у гэтую сiстэму ўваходзiць у левую i правую часткi. Для таго, каб пачаць iтэрацыйны працэс па формуле (19), неабходна спачатку выбраць так называемае пачатковае, або нулявое, наблiжэнне Х⁽⁰⁾, падставiць яго ў правую частку формулы (19) i вылiчыць першае наблiжэнне невядомай велiчынi X⁽¹⁾:

X⁽¹⁾=C+DX⁽⁰⁾.

Затым першае наблiжэнне X⁽¹⁾ зноў падстаўляецца ў правую частку раўнання (19) i вылiчваецца другое наблiжэнне X⁽²⁾:

X⁽²⁾=C+DX⁽¹⁾.

Працягвыючы гэты працэс, для k-ага наблiжэння маем:

X^(k)=C+DX^(k-1).                                                                                    (20)

Калi паслядоўнасць наблiжэнняў X⁽¹⁾, X⁽²⁾, ...X^(k) мае лiмiт, то гэты лiмiт з¢яўляецца рашэннем сiстэмы (2). Алгарытм (20) называецца алгарытмам iтэрацый для СЛАУ. У якасцi ўмовы для заканчэння iтэрацыйнага працэсу можна прыняць патрабаванне таго, каб найбольшая адносная рознасць (к)-ага i (к-1)-ага наблiжэнняў невядомай велiчынi X не перавышала некаторай наперад заданнай хiбнасцi ерs iтэрацыйнага працэсу:

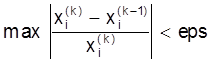.                                                                  (21)

Iтэрацыйны працэс характарызуецца такой важнай для яго ўласцiвасцю, як збежнасць. Толькi збежны iтерацыйны працэс можа прывесцi да атрымання рашэння сiстэмы (2). Умовамi збежнасцi iтэрацыйнага працэсу з¢яўляюцца, напрыклад, наступныя:

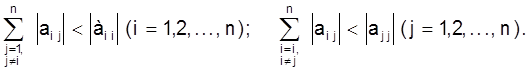   (22)

Модулi каэфiцыентаў, якiя знаходзяцца на галоўнай дыяганалi матрыцы каэфiцыентаў А, павiнны быць большымі сумы модуляў астатніх каэфiцыентаў у адпаведным радку або слупку матрыцы А.

Прыклад. Метадам простай iтэрацыi рашыць СЛАУ:

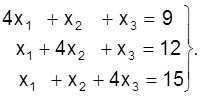
Умовы збежнасцi (22) для кожнага раўнання выконваюцца: для кожнага радка маем ½1½+½1½<½4½. Прыводзiм сiстэму да выгляду, зручнага для выканання iтэрацый:

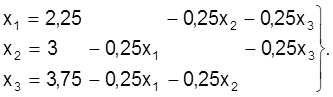                                          (23)

У якасцi пачатковага наблiжэння возьмем матрыцу C:

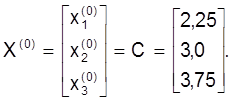
Першае наблiжэнне X⁽¹⁾ атрымаем, падставiўшы X⁽⁰⁾ у правую частку сiстэмы (23):

.

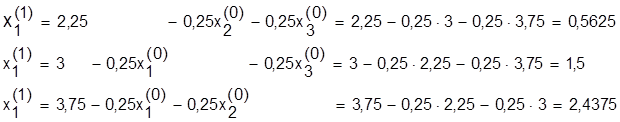Такiм чынам, першае наблiжэнне:

.

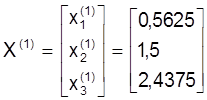Падстаўляем яго ў правую частку сiстэмы (23) i вылiчваем другое наблiжэнне:

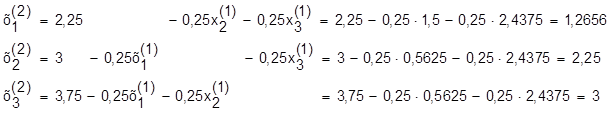
Або:

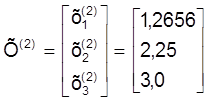
Прымяняючы гэты алгарытм, атрымаем наступныя наблiжэннi:

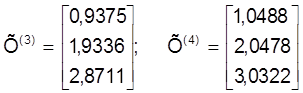
i так далей.

Дакладнае рашэнне сiстэмы:

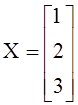
2.3.2. Метад Зэйдэля (метад палепшанай iтерацыі)

Метад Зэйдэля адрознiваецца ад метада простай iтэрацыi тым, што пры разлiку невядомай велiчынi  k-ага наблiжэння ў правую частку сiстэмы (23) падстаўляюцца пераменныя  k-ага наблiжэння, якiя ўжо вылiчаны на бягучым k-тым iтэрацыйным кроку з першага, другога, ... і-1 раунанняў , i пераменныя  k-1-ага наблiжэння, атрыманыя на папярэднiм iтэрацыйным кроку. Напрыклад, формулы для разлiку першага наблiжэння X⁽¹⁾ ў разгорнутай форме для сiстэмы трэцяга парадку маюць выгляд:

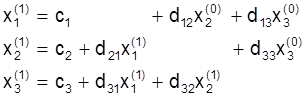
У большасцi выпадкаў метад Зэйдэля дае лепшую збежнасць iтэрацыйнага працэсу ў параўнаннi з метадам простай iтэрацыi.

Прыклад 5. Рашыць сiстэму прыкладу 4 метадам Зэйдэля.

Выкарыстоўваючы сiстэму (23) i нулявое наблiжэнне X⁽⁰⁾=C, атрымаем першае наблiжэнне X⁽¹⁾:

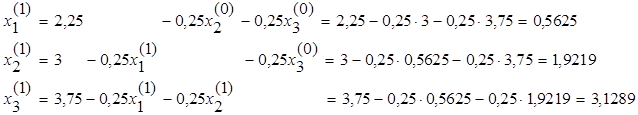
Прымяняючы паслядоўна алгарытм Зэйдэля, атрымаем:

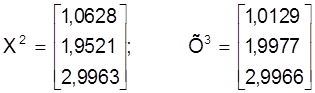
i так далей.

Параўноўваючы атрыманыя рэзультаты з дакладным рашэннем сiстэмы i з рэзультатамi метаду простай iтэрацыi, можна канстатаваць лепшую збежнасць метаду Зэйдэля ў параўнаннi з метадам простай iтэрцыi.

2.4. Праграмная рэалiзацыя дакладных i наблiжаных метадаў