Матэматычныя мадэлi ўсталяванага рэжыму (Лабараторная работа № 3)

            Беларуская дзяржаўная політэхнічная акадэмія

            Кафедра эдектрычных станцый

Матэматычныя задачы энергетыкі

Лабараторная работа № 3

Матэматычныя мадэлі ўсталяванага рэжыму

Аўтар Бобка М.М.

Мінск, 2000

Матэматычныя задачы энергетыкi

Лабараторная работа №3

Матэматычныя мадэлi ўсталяванага рэжыму

1 Мэта работы: азнаямленне з пабудовай i рэалiзацыяй матэматычных мадэляў усталяванага рэжыму.

2 Тэарэтычныя звесткi

Матэматычныя мадэлi ўсталяванага рэжыму электраэнергетыч-най сiстэмы будуюцца на аснове сiстэм лiнейных алгебраiчных раўнанняў. У гэтай рабоце разглядаюцца тры матэматычныя мадэлi ўсталяванага рэжыму:

- абагульненыя раўнаннi стану электрычнага ланцуга на аснове першага i другога законаў Кiрхгофа;

- вузлавыя раўнаннi;

- контурныя раўнаннi.

2.1. Абагульненае раўнанне стану на аснове законаў Кiрхгофа

Абагульненае раўнанне стану электрычнага ланцуга на аснове законаў Кiрхгофа мае выгляд [1]:

AI=F;                                                                          (1)

дзе 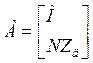       - квадратная матрыца m´m, дзе m - колькасць галін электрычнай схемы;

M - першая матрыца злучэнняў (інцыдэнцый), або вузлавая матрыца, памерам (n-1)´m, дзе n - колькасць усіх вузлоў схемы, а (n-1) - колькасць лінейна незалежных вузлоў схемы;

N - другая матрыца злучэнняў (інцыдэнцый), або контурная матрыца, памерам k´m, дзе k - колькасць лінейна незалежных контураў схемы;

Z_г - дыяганальная матрыца супраціўленняў галін схемы памерам m´m;

I- матрыца - слупок токаў у галінах схемы памерам m´1;

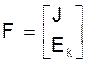 - матрыца - слупок правых частак абагульненага раўнання памерам m´1;

J - матрыца - слупок токаў крыніц тока ў незалежных вузлах схемы памерам (n-1)´1;

Е_к - матрыца - слупок контурных электрарухаючых сіл (ЭРС) ў лінейна незалежных контурах памерам k´1.

Пакажам на прыкладзе паслядоўнасць пабудовы абагульненага раўнання стану (1) у разгорнутай форме для мадэлявання ўсталяванага рэжыму ў схеме замяшчэння электрычнай сістэмы,

z1=0,1+j0,3;                z2=0,05+j0,4;  z3=0,1+j0,5;                e1=1,1+j0,0; z4=0,08+j0,4;  z5=0,1+j0,4;                z6=0,09+j0,5;  e6=1,3+j0,2; z7=1,5+j0,8;                z8=0,1+j0,5;                z9=0,2+j0,4;                j9=1,0-j2,0. а) схема замяшчэння і яе параметры ў адносных адзінках;   б) падграф дрэва;                                          в) падграф хорд. Мал.1. Схема замяшчэння для нармальнага рэжыму работы

прыведзенай на мал.1а. Схема мае пяць вузлоў (n=5), дзевяць галін (m=9) і пяць лінейна незалежных контураў: k=m-(n-1)=9-(5-1)=5.

Для таго, каб атрымаць сістэму абагульненых раўнанняў ўсталяванага рэжыму з ненулявымі дыяганальнымі элементамі, пабудуем правільны, або нармальны граф схемы замяшчэння. Падзел графа на падграфы дрэва і хорд можна выканаць некалькімі варыянтамі. У дрэва неабходна ўключыць усе вузлы і столькі галін, каб злучыць імі ўсе вузлы, але не ўтварыць замкнутых контураў. Базіснаму вузлу прысвойваем нумар 0, першы вузел далучаем да нулявога галіной нумар 1, другі вузел далучаем да дрэва галіной нумар 2, трэці вузел - галіной нумар 3 і г.д. Усе астатнія галіны і вузлы, якія не ўвайшлі ў падграф дрэва, ўваходяць ў падграф хорд. Галіны і вузлы падграфа хорд адвольна нумаруем узрастаючымі па парадку лічбамі. Адвольна выбіраем дадатныя накірункі галін (мал. 1б,в). Колькасць галін ў дрэве вызначае колькасць лінейна незалежных вузлоў у схеме замяшчэння, а колькасць галін у падграфе хорд - колькасць незалежных контураў у схеме замяшчэння. Першы контур утвараецца галіной 5, і накірунак яго выбіраецца супадаючым з накірункам галіны 5 (уносячы галіну 5 у дрэва, атрымоўваем першы контур з галінамі 5, 2, 3). Другі контур утвараецца галіной 6 і уключае галіны 6, 1, 2 і г.д.

Пабудуем усе матрыцы, якія ўваходзяць у раўнанне (1).

Першая матрыца злучэнняў М паказвае, як падключана j-тая галіна схемы да і-тага вузла: пачаткам (элемент m_ij матрыцы М роўны адзінцы), канцом (m_ij=-1) або не падключана зусім (m_ij=0). Вузел з нулявым нумарам выбіраем у якасці базіснага, ён з’яўляецца лінейна залежным вузлом, і для яго адпаведны радок у матрыцы М не запісваецца. Нумары супраціўленняў і крыніц у схеме адпавядаюць нумарам галін. Для схемы на мал.1 матрыца М мае выгляд:

.

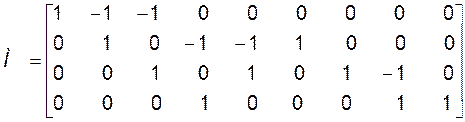Элементы n_ij матрыцы N паказваюць, ці ўваходзіць j-тая галіна схемы ў і-ты контур (n_ij=0, калі j-тая галіна ў і-ты контур не ўваходзіць) і ці супадае накірунак j-тай галіны з накірунам і-тага контура (n_іj=1 - cупадае; n_іj=-1 - не супадае):

.

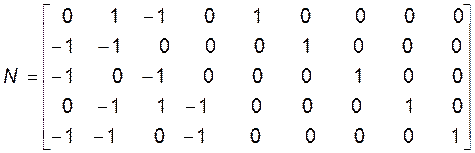Дыяганальная матрыца супраціўленняў галін схемы Z_г утрымлівае на галоўнай дыяганалі супраціўленні схемы, а недыяганальныя яе элементы роўны нулю:

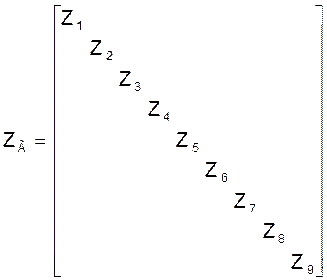
Матрыца - слупок невядомых токаў I ў галінах схемы мае m=9 радкоў:

Матрыца - слупок токаў J крыніц тока ў чатырох лінейна незалежных вузлах схемы:

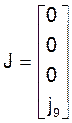
Матрыца - слупок контурых ЭРС сіл Е_к утрымлівае контурныя ЭРС пяці котураў:

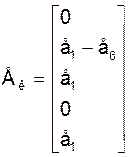
Здабытак двух матрыц NZ_г (ніжні блок матрыцы А ў формуле (1)) знойдзем ў адпаведнасці з правіламі перамнажэння двух матрыц: