Математика \ Математические задачи энергетики

Применение числовых методов в электротехнических расчетах

Страницы работы

27 страниц (Word-файл)
Посмотреть все страницы
Скачать файл

Фрагмент текста работы

Расчет токов короткого замыкания в ветвях схемы на основе законов Кирхгофа.

Расчет токов трехфазного короткого замыкания в ветвях схемы с помощью программы TKZ

Расчет переходного режима

Литература

Расчет параметров схемы замещения

Направления токов выбираем от узла с большим номером узла к узлу с меньшим номером.

Нумерация токов совпадает с нумерацией сопротивлений ветвей .

Например на Z5 течет ток I5

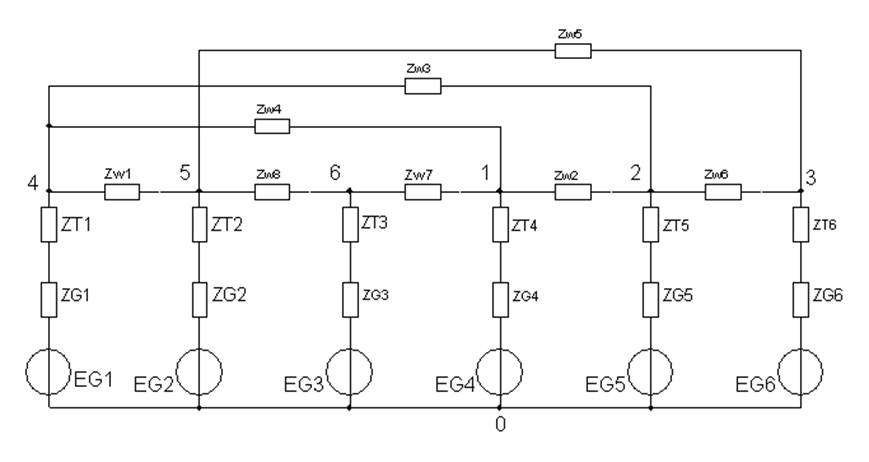
Контуры выбираем исходя из составленных дерев и хорд.

Генераторы

Таблица 1.

Обозначение

Тип

,

МВ×А

G1

2хТВС-32У3

40

2.648

0,153

0,8

G2

2хТВФ-120-2У3

125

1,907

0,192

0,8

G3

3хТВФ-320-2ЕУ3

375

1,698

0,173

0,85

G4

2хТВФ-63-2У3

78,75

1,2

0,153

0,8

G5

   ТВФ-110-2ЕУ3

137,5

2,04

0,189

0,8

G6

3хТГВ-200-2У3

235.3

1.84

0,189

0,8

Трансформаторы

Таблица 2.

Обозначение

Тип

,

МВ×А

,

%

Т1

2´ТДЦ-40 000/220

40

242/10,5

Т2

3´ТДЦ-125000/220

125

242/10,5

Т3

3´ТЦ-400000/220

400

242/20

Т4

2´ТД-80000/220

80

242/10,5

Т5

ТДЦ-125000/220

125

242/10,5

Т6

3´ТЦ-250 000/220

250

242/10,5

ЛЭП

Таблица 3.

Обозначение

Длина линии l, км

, Ом/км

W1

90

0,4

W2

100

0,4

W3

110

0,4

W4

110

0,4

W5

110

0,4

W6

120

0,4

W7

80

0,4

W8

110

0.4

Расчет будем вести в относительных единицах при  МВА и  кВ.

Схема замещения генератора представляется сопротивлением и ЭДС. В зависимости от режима работы сопротивление и ЭДС генератора имеют три разные значения. В установившемся режиме генератор заменяется установившемся сопротивлением  и установившейся ЭДС ; в переходном режиме – переходным сопротивлением  и переходной ЭДС ; для расчета токов короткого замыкания – сверхпереходным сопротивлением  и сверхпереходной ЭДС . Активное сопротивление генератора обычно не учитывают из-за его малости. Значения сопротивлений  и  представлены в таблице 1.

Значение ЭДС в установившемся режиме можно рассчитать по формуле:

.

Значит:

При режиме короткого замыкания значение ЭДС рассчитывается по выражению:

.

Тогда:

.

Расчет сопротивлений генераторов в установившемся режиме выполним по формуле:

.

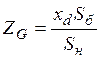Следовательно:

;

;

;

;

.

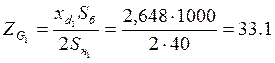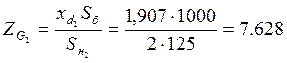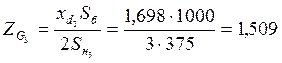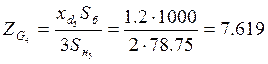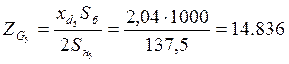
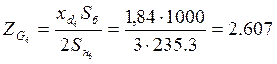Для режима короткого замыкания сопротивления генераторов находятся по следующей формуле:

.

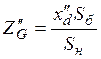Подставив значения параметров, получаем:

;

;

;

;

;

.

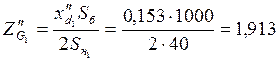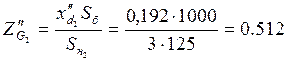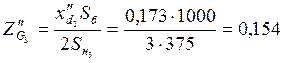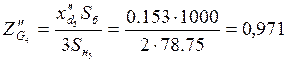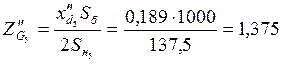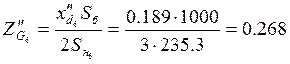Трансформаторы замещаются своим индуктивным сопротивлением, потому что для силовых трансформаторов активное сопротивление можно не учитывать. Рассчитаем сопротивления трансформаторов по выражению:

.

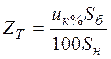Значит:

;

;

;

;

.

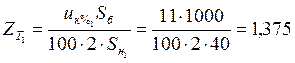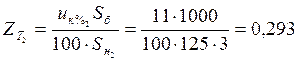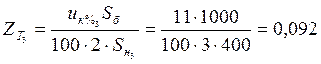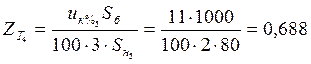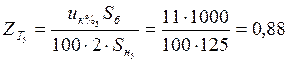
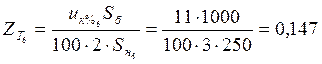Для воздушных ЛЭП обычно задается удельное индуктивное сопротивление . Сопротивление линии электропередачи найдем из

.

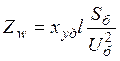Следовательно:

;

;

;

;

;

;

;

;

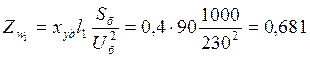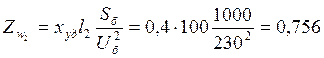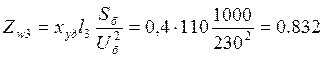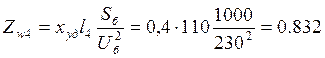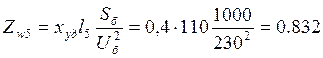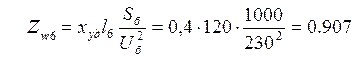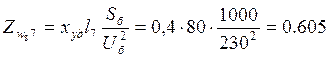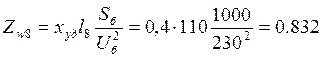Расчет токов установившегося нормального режима в ветвях схемы на основе модели контурных уравнений

 Составим систему контурных уравнений следующим образом:

На главной диагонали матрицы значения элементов будут равны сумме сопротивлений  в этом контуре.

На остальных  элементах значения будут равны сумме сопротивлений  при попадании одновременно в два контура.

Система контурных уравнений для схемы, представленной на рис. 1, будет иметь вид:

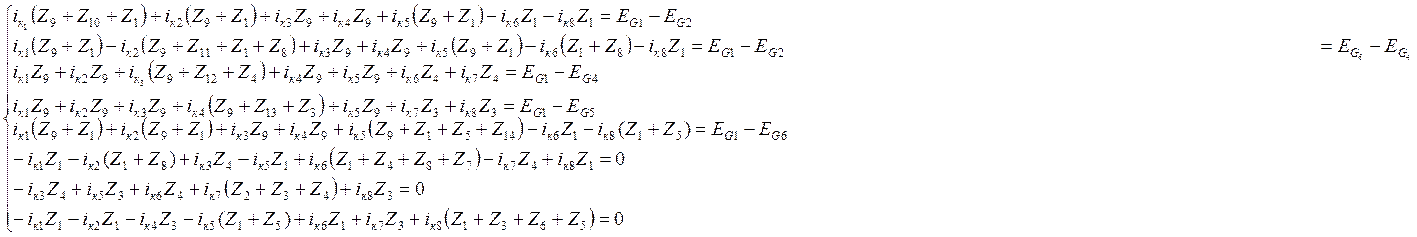
После подстановки значений параметров получаем:

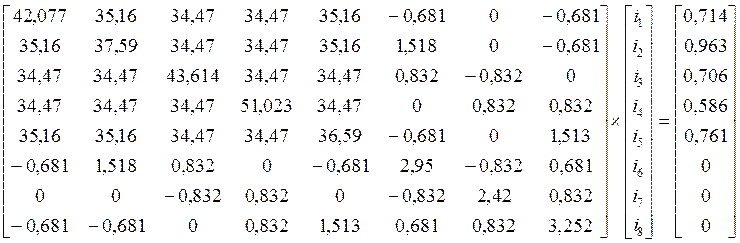
Решая числовым методом простой итерации, получаем:


I1k=0.021

I2k=0.00613

I3k=-0.0401

I4k=-0.0501

I5k= 0.0362

I6k=0.00471

I7k=0.0561

I8k=-0.00711


Тогда токи в ветвях схемы определяются через контурные согласно принципу наложения, как алгебраическая сумма контурных токов замыкающихся по данной ветви:


I1= -I1k-I2k-I5k     =  0.021-0.00613-0.0362=-0,0213

I2= I7k=0.0561

I3= I7k+I8k=0.0561-0.00711=0,0491

I4= I6k-I7k=0.00471-0.0561=-0,0514

I5= -I8k+I5k =0.00711+0.0362=0,0431

I6= -I8k=0.00711

I7= -I6k=-0.00471

I8= I5k-I2k=0.0362-0.00613=0,030

I9= -I1k-I2k-I3k -I4k -I5k=-0.021-0.00613+0.0401+0.0501-0.0362=0,0267

I10= I1k=0.021

I11= I2k=0.00613


I12= I3k=-0.0401

I13= I4k=-0.0501

I14= I5k=0.0362

Перейдем к именованным единицам:

                       

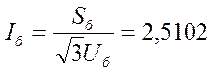
I1= I1 *Iб = -0,0213*2.51=-0,0534  (kA)  

I2= I2 *Iб =0,0561*2.51=0,148  (kA)  

I3= I3 *Iб =  0,0491*2.51=0,123  (kA)  

I4= I4 *Iб =  -0,0514*2.51=-0,129  (kA)  

I5= I5 *Iб = 0,0431*2.51=0,108  (kA)  

I6= I6 *Iб = 0,00711*2.51=0,0178  (kA)  

I7= I7 *Iб =  -0,00471*2.51=0,0118  (kA)  

I8= I8 *Iб = 0,030*2.51=0,0753  (kA)  

I9= I9 *Iб =  0,0267*2.51=0,067  (kA)  

I10= I10 *Iб = 0,021*2.51=0,0527  (kA)  

I11= I11 *Iб =  0,00613*2.51=0,0154  (kA)  

I12= I12 *Iб = -0,0401*2.51=-0,101  (kA)  

I13= I13 *Iб =-0,0501*2.51=-0,126  (kA)  

I14= I14 *Iб = 0,0362*2.51=0,091  (kA)  

Расчет токов установившегося нормального режима в ветвях схемы на основе уравнений по законам Кирхгофа.

Система уравнений будет иметь вид:

*  

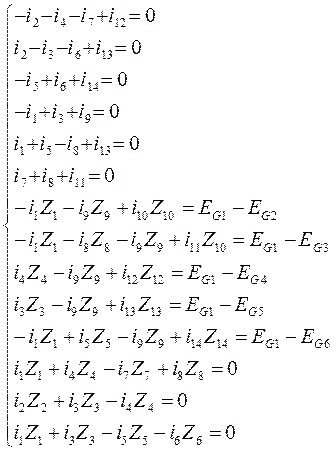
После подстановки значений, получим:

*  

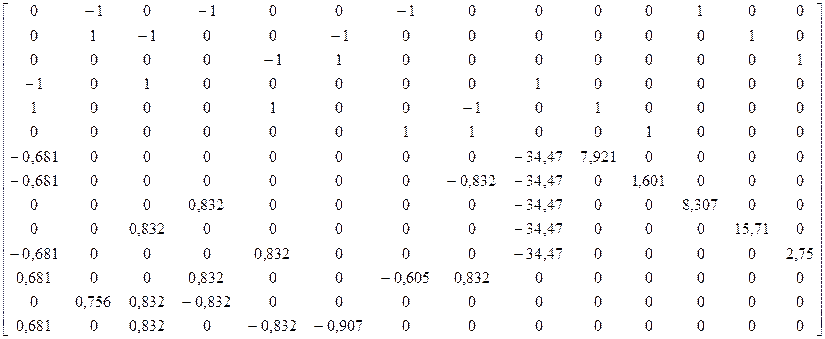
               Матрица ЭДС установившегося нормального режима

*   С помощью метода Жардана  , получим:

I1= -0,0211

I2= 0,0563

I3= 0,0495

I4= -0,0514

I5= 0,0413

I6= 0,00719

I7= -0,00479

I8= 0,0312

I9= 0,0271

I10= 0,0213

I11= 0,00601

I12= -0,0407

I13= 0,0491

I14= 0,0365

Составим баланс токов для 2 узла

-I6 +I2 +I13 =0

-0,00719+0,0563+0,0491=0

Перейдем к именованным единицам:

                       

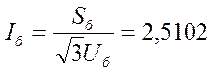
I1= I1 *Iб = -0,0211*2.51=-0,0529  (kA)  

I2= I2 *Iб =0,0563*2.51=0,141  (kA)  

I3= I3 *Iб =  0,0495*2.51=0,124  (kA)  

I4= I4 *Iб =  -0,0514*2.51=-0,130  (kA)  

I5= I5 *Iб = 0,0431*2.51=0,108  (kA)  

I6= I6 *Iб = 0,00719*2.51=0,0175  (kA)  

I7= I7 *Iб =  -0,00479*2.51=0,0118  (kA)  

I8= I8 *Iб = 0,0312*2.51=0,0757  (kA)  

I9= I9 *Iб =  0,0271*2.51=0,0681  (kA)  

I10= I10 *Iб = 0,0213*2.51=0,0529  (kA)  

I11= I11 *Iб =  0,00601*2.51=0,0150  (kA)  

I12= I12 *Iб = -0,0407*2.51=-0,103  (kA)  

I13= I13 *Iб =-0,0491*2.51=-0,117  (kA)  

I14= I14 *Iб = 0,0365*2.51=0,091  (kA)  

Расчет токов короткого замыкания в ветвях схемы на основе модели контурных уравнений

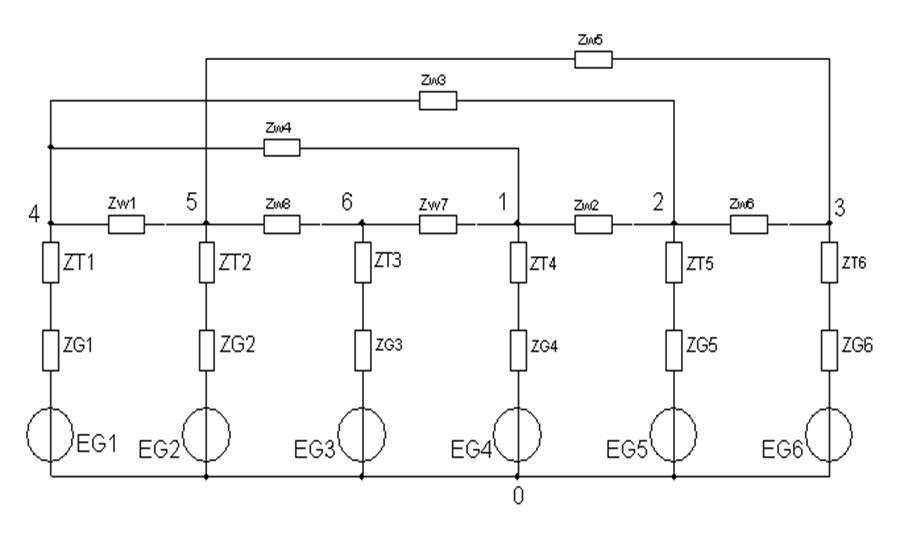
Рис 2. Схема замещения при коротком замыкании

Система контурных уравнений для схемы на рис. 2 будет следующей:

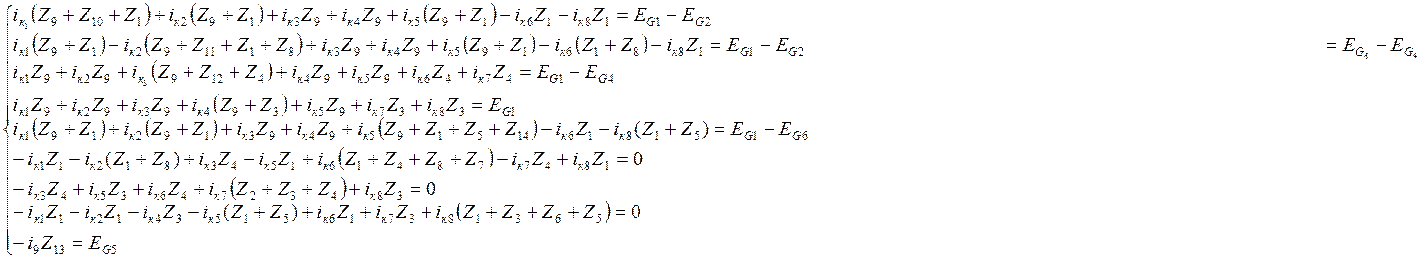
После подстановки значений параметров получаем:

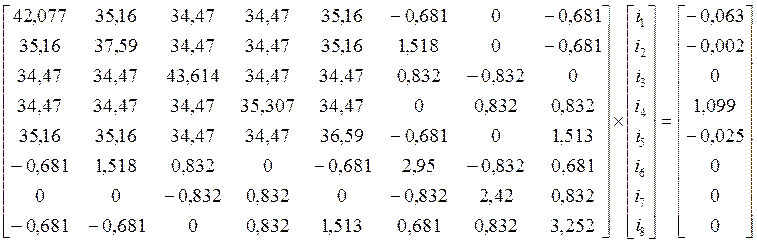
Дополним уравнением    

С помощью метода простой итерации, получим


I1k=0.114

I2k=0.261

I3k=0.123

I4k=0.501

I5k= 0.334

I6k=-0.211

I7k=0.314

I8k=-0.309

I9k=0.197


Токи в ветвях схемы определяются через контурные согласно принципу наложения:

I1= -I1k-I2k-I5k  =-0.167

I2= I7k=0.314

I3= I7k+I8k  =-0.239

I4= I6k-I7k  =0.0279

I5= -I8k+I5k =-0.152

I6= -I8k  =-0.309

I7= -I6k  = -0.211

I8= I5k-I2k  =-0.0581

I9= -I1k-I2k-I3k -I4k -I5k=0.0654

I10= I1k=0.114

I11= I2k=0.261

I12= I3k=0.123

I13= I9k=0.197

I14= I5k=0.334

  Перейдем к именованным единицам:

                       

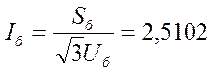
I1= I1 *Iб = -0.167*2.51=-0.408  (kA)  

I2= I2 *Iб =0.314*2.51=0.781  (kA)  

I3= I3 *Iб =  -0.239*2.51=-0.607  (kA)  

I4= I4 *Iб =  0.0279*2.51=0.0718  (kA)  

I5= I5 *Iб = -0.152*2.51=-0.393 (kA)  

I6= I6 *Iб = -0.309*2.51=-0.787  (kA)  

I7= I7 *Iб =  -0.211*2.51=-0.525  (kA)  

I8= I8 *Iб = -0.0581*2.51=-0.146  (kA)  

I9= I9 *Iб =  0.0654*2.51=0.167  (kA)  

I10= I10 *Iб = 0.114*2.51=0.286  (kA)  

I11= I11 *Iб =  0.261*2.51=0.655  (kA)  

I12= I12 *Iб = 0.123*2.51=0.315  (kA)  

I13= I13 *Iб = 0.197*2.51=0.491  (kA)  

I14= I14 *Iб = 0.334*2.51=0.820  (kA)  


Расчет токов короткого замыкания в ветвях

схемы на основе законов Кирхгофа.

Система уравнений будет иметь вид:

*  

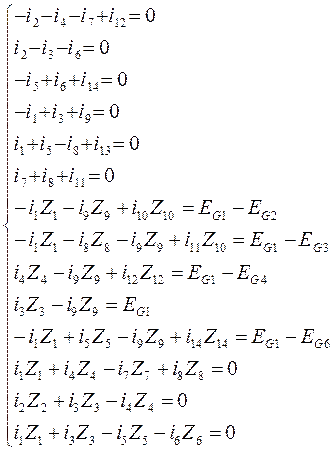
После подстановки значений, получим:

*  

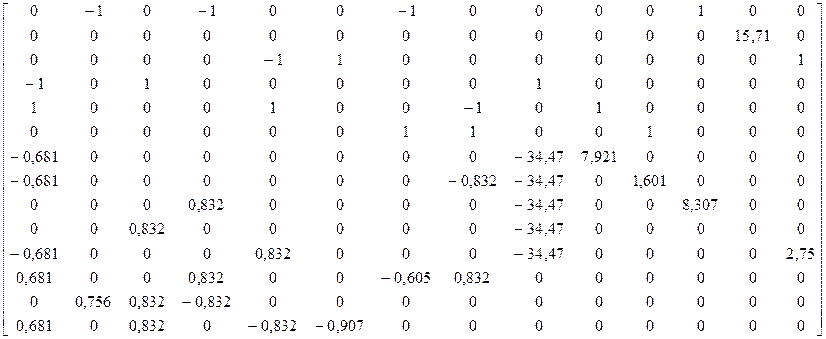
Матрица ЭДС при коротком замыкании

                                                                                                       

*     С помощью метода Жардана  , получим:

I1= -0.162

I2= 0.310

I3= -0.241

I4= 0.0285

I5= -0.158

I6= -0.315

I7= -0.209

I8= -0.0587

I9= 0.0641

I10= 0.114

I11= 0.261

I12= 0.125

I13= 0.194

I14= 0.324

Перейдем к именованным единицам:

                       

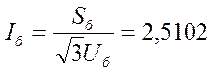
I1= I1 *Iб = -0.162*2.51=-0.406  (kA)  

I2= I2 *Iб =0.310*2.51=0.778  (kA)  

I3= I3 *Iб =  -0.241*2.51=-0.602  (kA)  

I4= I4 *Iб =  0.0285*2.51=0.0721  (kA)  

I5= I5 *Iб = -0.158*2.51=-0.397  (kA)  

I6= I6 *Iб = -0.315*2.51=-0.790  (kA)  

I7= I7 *Iб =  -0.209*2.51=-0.524  (kA)  

I8= I8 *Iб = -0.0587*2.51=-0.145  (kA)  

I9= I9 *Iб =  0.0641*2.51=0.161  (kA)  

I10= I10 *Iб = 0.114*2.51=0.286  (kA)  

I11= I11 *Iб =  0.261*2.51=0.655  (kA)  

I12= I12 *Iб = 0.125*2.51=0.313  (kA)  

I13= I13 *Iб = 0.194*2.51=0.487  (kA)  

I14= I14 *Iб = 0.324*2.51=0.813  (kA)  


Расчет токов трехфазного короткого замыкания в ветвях схемы с помощью программы TKZ

*              В Ы Х А Д Н Ы   Ф А Й Л   П Р А Г Р А М Ы   TKZ

УВАХОДНЫЯ ДАДЗЕНЫЯ:

Прызнак разлiку каэфiцыентау размеркавання токау КЗ

па галiнах схемы NRKRTKZH=2

Прызнак схемы нулявой паслядоунасцi NSNP=0

Колькасць галiн у схеме прамой паслядоунасцi KH=14

Колькасць вузлоу кароткага замыкання KWKZ= 1

Колькасць галiн у схеме нулявой паслядоунасцi KHSNP= 0

Колькасць вузлоу у схеме нулявой паслядоунасцi, якiя маюць нулявы патэнцыял KWSNPNP= 0

Базiсная магутнасць SB= 1000. MVA

Iнфармацыя аб галiнах схемы прамой паслядоунасцi:

N1K(KH) N2K(KH)    X(KH)      SNG(KH)

адн.адз.      МВА

0      1     1.6590        158.

0      2     2.2550        138.

0      3      .4150        706.

0      4     3.2880         80.

0      5      .8050        250.

0      6      .2460       1125.

1      2      .7560          0.

1      4      .8320          0.

1      6      .6050          0.

2      3      .9070          0.

2      4      .8320          0.

3      5      .8320          0.

4      5      .6810          0.

5      6      .8320          0.

Iнфармацыя аб вузлах кароткага замыкання:

NWKZ(KWKZ)   UB(KWKZ)

кВ

2        230.0

РЭЗУЛЬТАТЫ РАЗЛIКУ:

НУМАР ВУЗЛА  КЗ:    2

Базiснае напружанне вузла КЗ, кВ:     230.000000

Базiсны ток у вузле КЗ, кА:       2.510219

Рэзультатыунае супрац. схемы адносна вузла КЗ:

-для токау прамой (адв.) паслядоун. (адн.адз.)  3.990385E-01

Перыядычная састаул. звышпераходн. току КЗ (КА):

- трохфазнае       6.290668

- двухфазнае       5.447879

Сiметрычныя састауляльныя току КЗ (КА):

Прамая      Адваротная  Нулявая

- трохфазнае      6.2907

- двухфазнае      3.1453      3.1453

Каэфiцыенты размеркавання сiметрычныых састауляльных тока КЗ па   галiнах схемы (дадатным накiрункам у галiне лiчыцца накiрунак   ад канца галiны з большым нумарам да канца з меньшым нумарам)

Галiна схемы      Прамая   Адваротная     Нулявая

           0    1      -.1109       .1109

           0    2      -.1770       .1770

           0    3      -.2917       .2917

           0    4      -.0627       .0627

           0    5      -.1025       .1025

           0    6      -.2554       .2554

           1    2      -.2845       .2845

           1    4      -.0265       .0265

           1    6       .2002      -.2002

           2    3       .3065      -.3065

           2    4       .2320      -.2320

           3    5       .0148      -.0148

           4    5       .1428      -.1428

           5    6       .0552      -.0552

Для ЛЭП  UH=230 В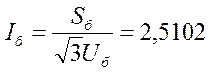   

Тогда токи

I1=I45*Iб=-0.1428*6.2907=-0.893     (kA)    

I2=I12*Iб=02845*6.2907=1.789 (kA)

I3=I24*Iб=-0.232*6.2907=-1.459  (kA) 

I4=I14*Iб=0.0265*6.2907=-0.1667  (kA) 

I5=I35*Iб=-0.0148*6.2907=-0.0931  (kA) 

I6=I23*Iб=-0.3065*6.2907=-1.928  (kA) 

I7=I16*Iб=-0.2002*6.2907=-1.259  (kA) 

I8=I56*Iб=-0.0552*6.2907=0.347  (kA) 

I9=I04*Iб=0.0627*6.2907=0.394  (kA) 

I10=I05*Iб=0.1025*6.2907=0.645  (kA) 

I11=I06*Iб=0.2554*6.2907=1.607  (kA) 

I12=I01*Iб=0.1109*6.2907=0.697  (kA) 

I13=I02*Iб=0.177*6.2907=1.113  (kA) 

I14=I14*Iб=0.2917*6.2907=0.1834  (kA) 

Различие между токами найденными разными методами незначительно , поэтому считаем расчет верным.

Расчет переходного режима

Требуется рассчитать числовым методом токи в ветвях схемы и напряжения на ветвях схемы в переходном режиме, который возникает после замыкания ключа К в схеме, представленной на рис. 3.

С1 = 80 мкФ;

C3 = 20 мкФ;

L = 0.5 Гн;

R1 = 5 Ом;

R2 = 35 Ом;

R3 = 5 Ом;

е1 = Емsin(wt+j);

Ем = 200 B;

w = 314 р/с;

j = 45°.
 


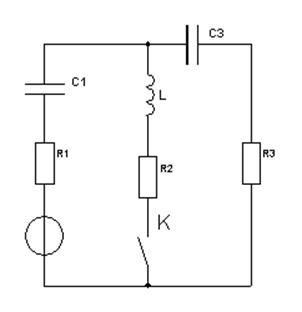
Рис. 3. Схема замещения энергосистемы для расчета переходного режима

После замыкания ключа в схеме образуется два линейно независимых контура и один линейно независимый узел.

Получим систему следующего вида:

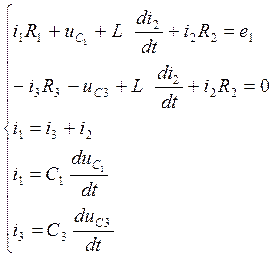.                                (1)

Для того ,чтобы привести систему дифференциальных уравнений к нормальному виду сделаем следущее :

От первого  уравнения (1)  системы отнимем второе

        (2)

 Для того ,чтобы получить  подставим  в  (2)

 

                 (*)

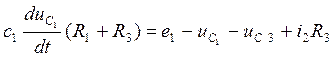
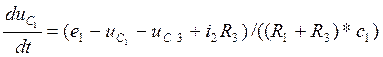анологично для 

               (*)

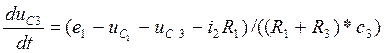Выразим 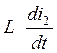 из первого уравнения системы  (1)

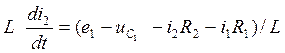
т.к. 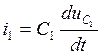    то   (*)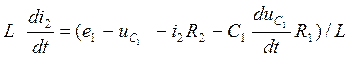

Систему дифференциальных уравнений составим из уравнений  с (*) , она выглядит следующим образом:

.

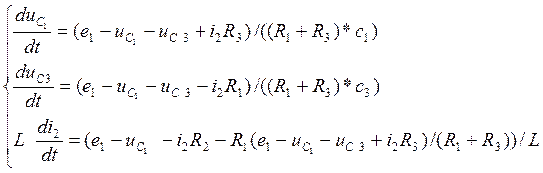Рассчитаем начальные условия. До замыкания ключа в схеме имелся один контур, поэтому:

;

;

;

;

;

.

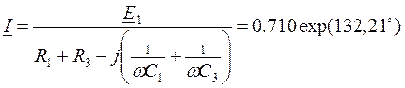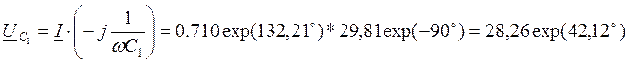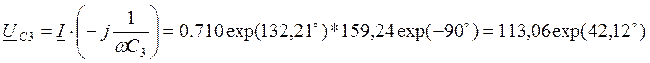По результатам расчета построим векторную диаграмму напряжений для установившегося доаварийного режима. Диаграмму токов строить не имеет смысла, так в схеме до замыкания ключа всего один контур, а следовательно и один ток.

 Векторная диаграмма напряжений установившегося

доаварийного режима.

Теперь найдем начальные условия  и .

Из  получаем .

Тогда в момент времени t = 0

=26,80.

                        

Зная начальные условия можно решать систему дифференциальных уравнений. Числовое решение системы выполним при помощи программы решения системы дифференциальных уравнений методом Рунге-Кутта четвертого порядка (программа DIFRK4 в лабораторной работе № 7). Необходимо сделать адоптацию этой программы для решения системы. Изменения заключаются в следующем:

а) пишется новая подпрограмма PRAV для вычисления правых частей;

б) в программу PRAV включаются формулы для расчета токов i1, i3 и напряжений uR1, uR2, uR3, uL;

в) дополняется головной модуль программы оператором ввода параметров схемы R1, R2, R3, L, C1, C3 и заданных параметров режима схемы Em1, j1, w;

г) дополняется головная программа оператором COMMON для передачи параметраў R1, R2, R3, L, C1, C3, Em1, j1, w из головной программы в подпрограмму PRAV и для передачи параметров i1, i3, uR1, uR2, uR3, uL, e1 из подпрограммы PRAV в головную программу;

д) дополняется головная программа оператором вывода параметров режима i1, i3, uR1, uR2, uR3, uL, e1 в выходные файлы с расширением REZ и GRA.

Файл входных данных для моделирования переходного режима в схеме на рис. 3 после замыкания ключа К имеет вид:

3 20 0. 0.2 0.00002

26,80  107,24 0,0

200. 45. 5. 35. 5. 0.5 0.00008  0.00002 314.

Результаты расчета переходного процесса выводятся программой в виде столбцов с данными в файл с расширением REZ и GRA.

Подпрограмма правых частей для системы дифференциальных уравнений (3) будет иметь вид:

SUBROUTINE PRAV(X,Y,F)

REAL   L,I1,I3

DIMENSION Y(*),F(*)

COMMON EM1,F1,R1,R2,R3,L,c1,c3,OMEGA,

*I1,I3,UR1,UR2,UR3,UL,E1

E1=EM1*SIN(OMEGA*X+F1/57.2958)

F(1)= (1./(C1*(R1+R3)))*(E1-Y(1)-Y(2)+Y(3)*R3)

F(2)=(1./(C3*(R1+R3)))*(E1-Y(1)-Y(2)-Y(3)*R1)

F(3)=(1./L)*(E1-(E1-Y(1)-Y(2)+Y(3)*R3)R1/(R1+R3) -Y(1)-Y(3)*R2)

I1=C1*F(1)

I3=C3*F(2)

UR1=I1*R1

UR2=Y(3)*R2

UR3=I3*R3

UL=L*F(3)

RETURN

END

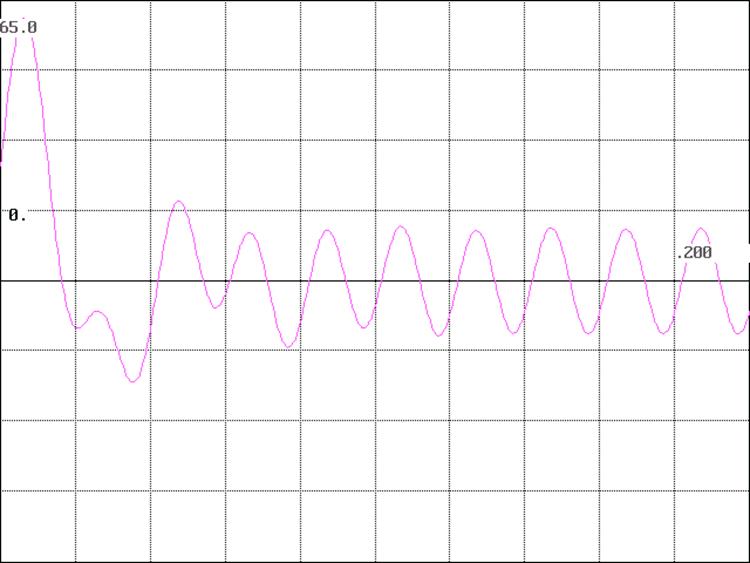
 График функции Uc1

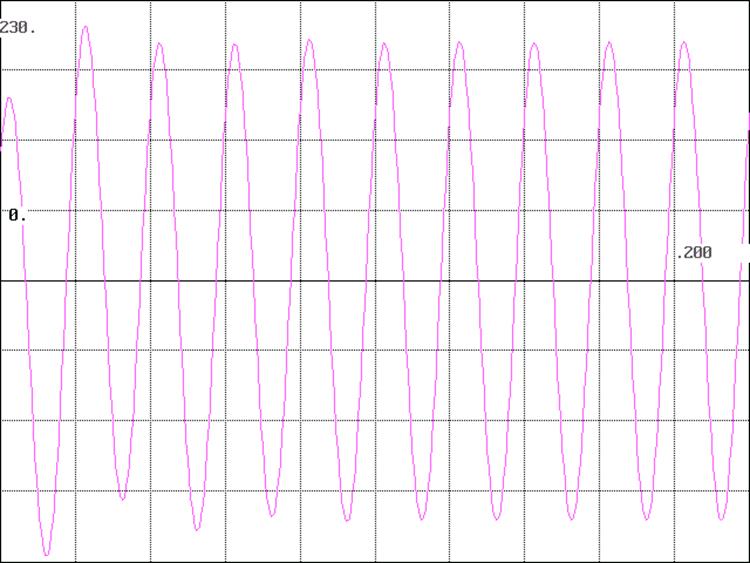
График функции Uc3

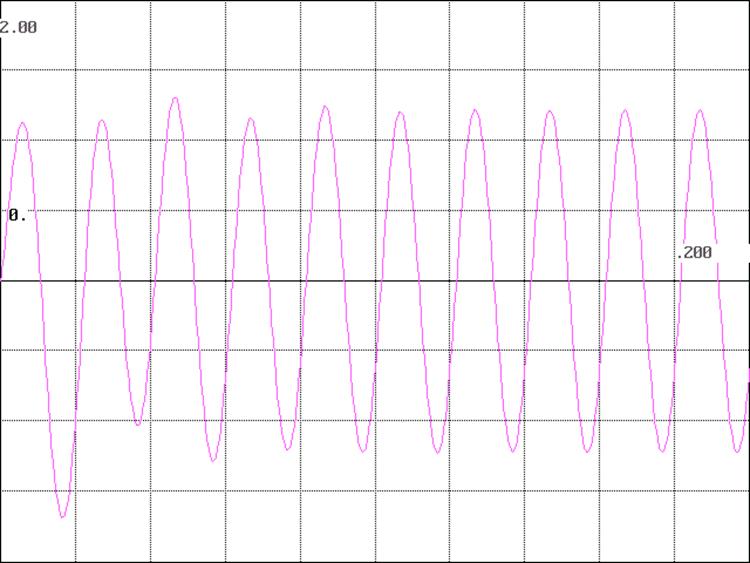График функции IL

После прекращения переходного режима в электрической схеме устанавливается установившийся послеаварийный режим. Это можно использовать для проверки правильности числового решения дифференциальных уравнений. Для этого необходимо рассчитать каким-нибудь методом установившийся послеаварийный режим и сравнить полученные комплексные значения параметров с мгновенными значениями соответствующих параметров, которые

Похожие материалы

Информация о работе

ВУЗ:
Белорусский национальный технический университет (БНТУ)
Предмет:
Математические задачи энергетики
Тип:
Курсовые работы
Категория:
Математика (Естествознание)
Размер файла:
438 Kb
Скачали:
0
Скачать файл