Парадак гэтай сiстэмы вызначаецца колькасцю лiнейна незалежных котураў схемы (к=5). У гэтай сістэме, у адпаведнасці з прынятай мадэллю (5), крыніца тока j9 у галіне 9 заменена крыніцай ЭРС е9=j9z9.
2.5 Разлiк токаў у галiнах схемы пры выкарыстаннi мадэляў на аснове вузлавых i контурных раўнанняў
Сiстэмы раўнанняў на аснове законаў Кірхгофа (1), на аснове вузлавых раўанняў (3) і на аснове контурных раўнанняў (5) з'ўяляюцца трыма асноўнымi матэматычнымi мадэлямi ўсталяванага рэжыму электрычнай сiстэмы. Парадак сiстэм (3) i (5) значна нiжэйшы, чым парадак сiстэмы (1), таму матэматычныя мадэлі (3) i (5) на практыцы прымяняюцца значна часцей, чым мадэль (1).
Токі ў галінах схемы ў мадэлі (1) непасрэдна выначаюцца як рашэнні сістэмы (1).
Токі ў галінах схемы ў мадэлі (3) на аснове вызлавых раўнанняў пры вядомых вузлавых напружаннях UВ можна разлічыць па наступных формулах, улічваючы, што вузлавое напружанне uВ0 нулявога вузла прынята роўным нулю:
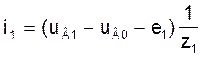
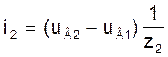
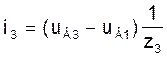
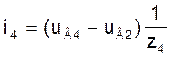
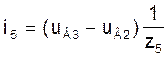
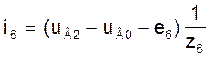(7)
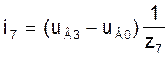
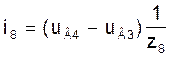
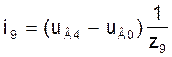
Токі ў мадэлі (5) на аснове контурных раўнанняў ў галінах 5, 6, 7, 8, 9, якія з’яўляюцца хордамі, ёсць контурныя токі ік1, ік2, ік3, ік4, ік5:
і5=ік1; і6=ік2; і7=ік3; і8=ік4; і9=ік5. (8а)
Токі ў галінах 1, 2, 3, 4, якія ўваходзяць ў дрэва, можна разлічыць па формулах:
і1=-ік2-ік3-ік5; і2=ік1-iк2-ік4-ік5;
і3=-ік1-ік3+ік4; і4=-ік4-ік5. (8б)
2.6 Матэматычныя мадэлi (1), (3), (5) пры наяўнасцi кароткага замыкання (КЗ) у адным з вузлоў схемы
Пасля затухання пераходных састаўляльных наступае ўсталяваны рэжым кароткага замфкання (КЗ), разлiк параметраў якога з'яўляецца важным для практыкi i можа быць выкананы на аснове мадэляў усталяванага рэжыму.
Наяўнасць КЗ у вузле 4 схемы на
мал.2 змяняе тапалагiчныя параметры схемы ў параўнаннi з дааварыйным рэжымам
(гл. схему на мал.1). Колькасць галiн застаецца ранейшай (m=9). Колькасць
незалежных вузлоў памяньшаецца на адзiн (n=3), таму што чацвёрты i нулявы вузлы
злiваюцца ў адзiн вузел. Колькасць контураў узрастае на адзiн (к=6), таму што
перамычка КЗ замыкае накаротка галiну 9 i ўтварае новы контур. У месцы КЗ схема
падзяляецца на дзве незалежныя часткі: коратказамкнутую галіну 9 і астатнюю
частку схемы. Сiстэма абагульненых раўнанняў стану па законах Кiрхгофа мае
выгляд: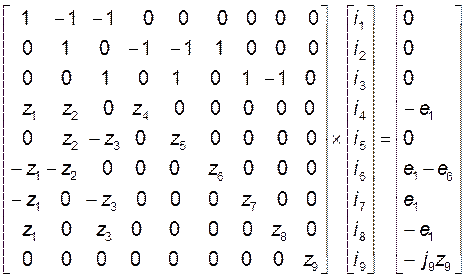
. (9)
У сістэме (9) ўтварае контур, у якім крыніца тока j9 заменеа крыіцай ЭРС е9=j9z9.
Вузлавыя раўнаннi для схемы на мал.2 маюць выгляд (для вузлоў 1, 2, 3):
 |
||||||
 |
||||||
 |
||||||
 |
||||||
|
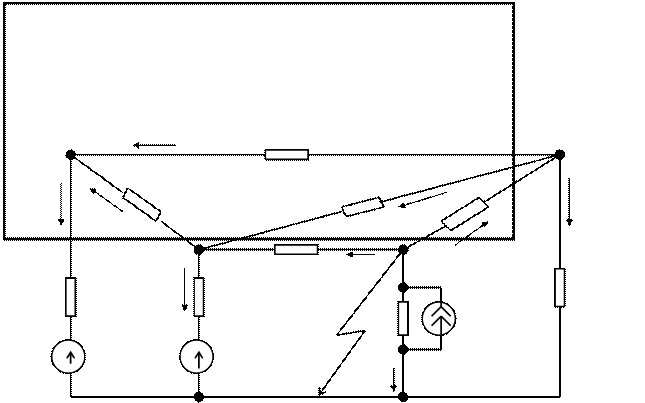
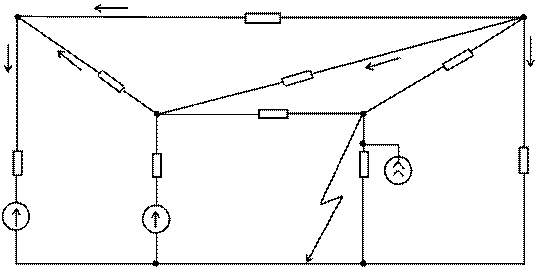
z1=0,1+j0,3; z2=0,05+j0,4; z3=0,1+j0,5; e1=1,1+j0,0; z4=0,08+j0,4; z5=0,1+j0,4; z6=0,09+j0,5; e6=1,3+j0,2; z7=1,5+j0,8; z8=0,1+j0,5; z9=0,2+j0,4; j9=1,0-j2,0. а) схема замяшчэння і яе параметры ў адносных адзінках;
б) падграф дрэва; в) падграф хорд. Мал.2. Схема замяшчэння для аварыйнага рэжыму работы |
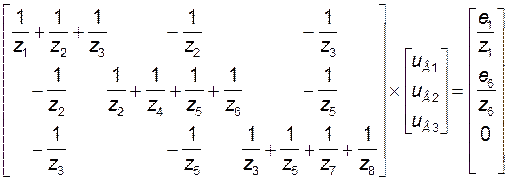. (10)
Контурныя раўнаннi для схемы на мал.2 запiсваюцца для контураў, утвораных галiнамi 4, 5, 6, 7, 8, 9:
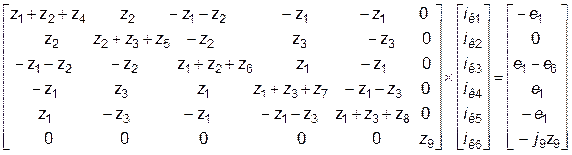(11)
2.7 Лiкавае рашэнне сiстэм (2), (4), (6), (9), (10), (11)
2.7.1 Рашэнне сiстэмы (2) абагульненыых раўнанняў стану для нармальнага рэжыму работы схемы на мал.1
Сiстэма абагульненых раўнанняў стану (2) з камплекснымi значэннямi каэфiцыентаў i правых частак для нармальнага рэжыму работы схемы на мал.1 мае выгляд
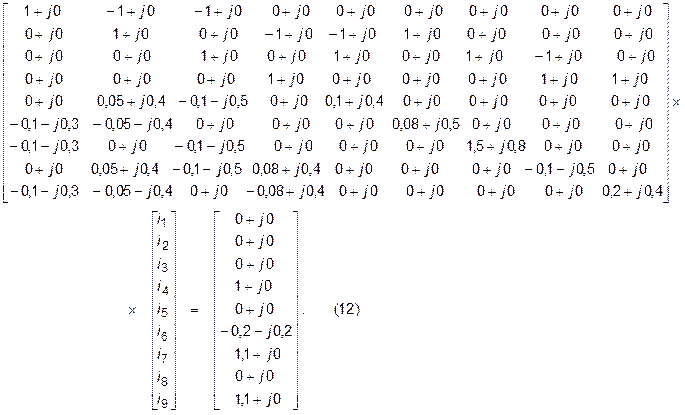
Рашэнне гэтай сістэмы магчыма толькі дакладнымі лікавымі метадамі, таму што ўмовы збежнасці ітэрацыйнага працэсу для яе не выконваюцца. Выканаем рашэнне раўнанняў (12) метадам Гаўса (праграма GAUSC для рашэння сістэмы лінейных алгебраічных раўнанняў з камплекснай матрыцай каэфіцыентаў). Файл уваходых дадзеных будзе мець выгляд (kirn.dat):
9
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
