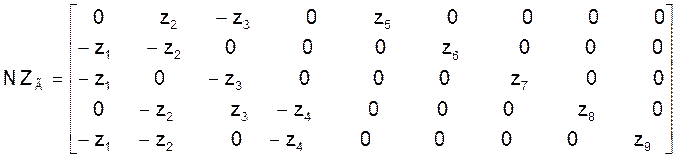Матэматычныя мадэлi ўсталяванага рэжыму (Лабараторная работа № 3), страница 2

.

Тады раўнанне (1) у разгорнутай форме для схемы на мал.1 будзе мець выгляд:

i₁-        i₂                -i₃                                                                                =0

i₂                                    -i₄             -i₅             +i₆                                                                        =0

i₃                                    +i₅                                +i₇            -i₈                                 =0

i₄                                                                            +i₈            +i₉            =j₉

i₂z₂          -i₃z₃                            +i₅z₅                                                                                       =0

-i₁z₁        -i₂z₂                                                                    +i₆z₆                                                                   =e₁-e₆   (2)

-i₁z₁                            -i₃z₃                                                                    +i₇z₇                                               =e₁

-i₂z₂        +i₃z₃       -i₄z₄                                                                    +i₈z₈                           =0

-i₁z₁        -i₂z₂                            -i₄z₄                                                                                        +i₉z₉       =e₁

Першыя чатыры раўнанні сістэмы (2) - гэта раўнанні першага закона Кірхгофа для вузлоў 1, 2, 3, 4, а апошнія пяць - гэта раўнанні другога закона Кірхгофа для контураў 1, 2, 3, 4, 5. Пры гэтым ток крыніцы тока j₉ увайшоў у матрыцу J (правая частка вузлавых раўнанняў), а ЭРС е₁ і е₆ - у матрыцу Е_к (правая частка контурных раўнаняў).

2.2 Вузлавыя раўнанні

Вузлавыя раўнанні звязваюць невядомыя вузлавыя напружанні з зададзенымі параметрамі схемы і зададзенымі параметрамі рэжыму схемы. Сістэма вузлавых раўнанняў у матрычнай форме мае выгляд [1,2]:

Y_вU_в=J-MY_вЕ.

Калі ўсе крыніцы электрычнай схемы прадставіць ў выглядзе крыніц тока (матрыца ЭРС галін схемы Е=0), то сістэма раўнанняў для вузлавых напружаняў спрашчаецца:

Y_вU_в=J                                                                        (3), дзе       Y_в - матрыца вузлавых праводнасцей схемы памерам (n-1)´(n-1) (n-колькасць вузлоў схемы); элемент y_ii матрыцы Y_в, які знаходзіцца ў і-тым радку на галоўнай дыяганалі, роўны суме праводнасцей галін, падключаных да і-тага вузла схемы (уласная праводнасць і-тага вузла); элемент y_ij на перакрыжаванні і-тага радка і j-тага слупка матрыцы Y_в роўны ўзятай са знакам мінус праводнасці галіны, уключанай паміж i-тым і j-тым вузламі схемы (узаемная праводнасць паміж i-тым і j-тым вузламі)

;

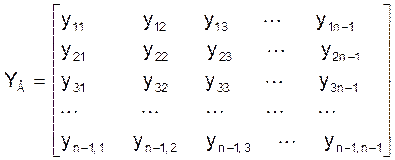U_в - матрыца - слупок памерам (n-1)´(n-1) невядомых вузлавых напружанняў у лінейна незалежных вузлах схемы:

;

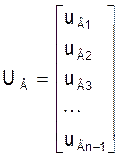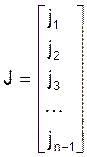
J - матрыца - слупок памерам (n-1)´1 токаў крыніц тока, якія дзейнічаюць у незалежных вузлах схемы (дадатны накірунак токаў - ад вузла):

.

Сістэма вузлавых раўнанняў (3) для схемы на мал.1 будзе мець выгляд:

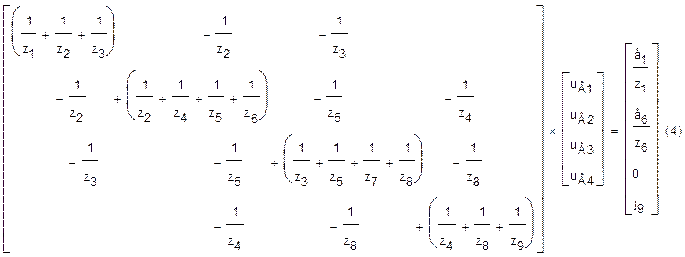            У гэтай сістэме, у адпаведнасці з прынятай мадэллю (3), ЭРС у галінах 1 і 6 заменены крыніцамі тока j₁ і j₆:

2.4 Контурныя раўнаннi

Контурныя раўнаннi ў матрычнай форме маюць выгляд [1,2]:

.

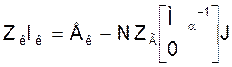Для схемы, у якой усе крынiцы электрычнай энергii прадстаўлены крынiцамi ЭРС (матрыца токаў крыніц тока J=0), гэтыя раўнанні спрашчаюцца:

Z_кI_к=Е_к                                                                       (5)

дзе:     Z_к - матрыца контурных супраціўленняў:

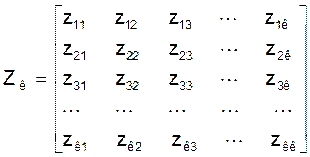, якая мае парадак к (колькасць лінейна незалежных контураў схемы). Дыяганальны элемент z_ii гэтай матрыцы роўны суме супраціўленняў галін, якія ўваходзяць у i-ты контур. Недыяганальны элемент z_ij роўны суме супраціўленняў галін, якія ўваходзяць адначасова ў i-ты і ў j-ты контуры, прычым сума мае знак плюс, калі накірункі і-тага і j-тага контураў у гэтых галінах супадаюць, і знак мінус,. калі не супадаюць.

I_к - матрыца - слупок невядомых контурных токаў памерам к´1:

;

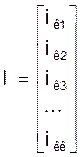Z_к - матрыца - слупок зададзеных контурных ЭРС памерам к´1:

.

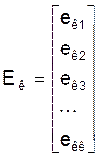Для схемы на мал.1а сiстэма контурных раўнанняў (5) у разгорнутай форме мае выгляд:

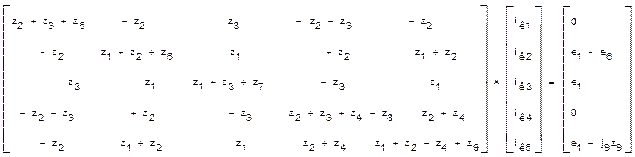     (6)