Матэматычная мадэль сінхроннага генератара (Лабараторная работа № 10)

Беларускі нацыянальны тэхнiчны ўніверсітэт

Кафедра “Электрычныя станцыі”

Дысцыпліна: Матэматычныя задачы энергетыкі

Лабараторная работа №10

Матэматычная мадэль сінхроннага генератара

Мінск 2006

1 Мэта работы

Мэтай работы з’яўляецца набыццё навыкаў даследвання рэжыму кароткага замыкання (КЗ) сінхроннага генератара на аснове лікавага рашэння дыферэнцыяльных і алгебраічных раўнанняў.

2 Кароткія тэарэтычныя звесткі

2.1 Прынцып работы сінхроннага генератара

Генератар- сінхронная электрычная машына, якая пераўтваре механiчную энергiю паравой або гiдраўлiчнай турбiны ў электрычную энергію. У пазах цыліндрычнага шыхтаванага статара (якара) ўкладзена трохфазная сілавая абмотка АХ, ВУ, BZ (мал 1). На ротары (індуктары) знаходзіцца абмотка ўзбуджэння, у якую ад знешняй крыніцы падаецца пастаянны ток узбуджэння. Ротар аварочваецца паравой або гідраўлічнай турбiнай. Абмотка ўзбуджэння стварае ў паветраным зазоры машыны магнітнае поле, якое індуктуе ў абмотцы статара пераменную электрарухаючу сілу (ЭРС) статара. Калі да абмоткi статара падключана нагрузка, то па ей працякае пераменны ток. Гэты ток, у сваю чаргу, стварае ў паветраным зазоры свае магнітнае поле (поле рэакцыі статара), якое складваецца з полем абмоткі ўзбуджання, у выніку чаго ствараецца вынiковае поле машыны, якое рухаецца ў паветраным зазоры сінхронна з ротарам. У машынах малой магутнасці ротар выконваецца яўнаполюсным і валодае магнітнай і электрычнай неіметрыяй. У машынах вялікай магутнасці абмотка ротара ўкладзена ў пазы ротара, які мае цыліндрычную форму i валодае магнiтнай сiметрыяй. У гэтым выпадку ротар валодае толькі электрычнай несіметрыяй. У абодвух выпадках ротар з’яуляецца несіметрычным, і з ім звязваюць падоўжную d і папярэчную q восі сіметрыі (гл. мал.1). Акрамя абмоткі ўзбуджэння, на ротары знаходзіцца таксама падоўжная w_эd і папярэчная w_эq каротказамкнёныя супакаяльныя абмоткі, якія забяспечваюць устойлівасць работы сінхроннай машыны.

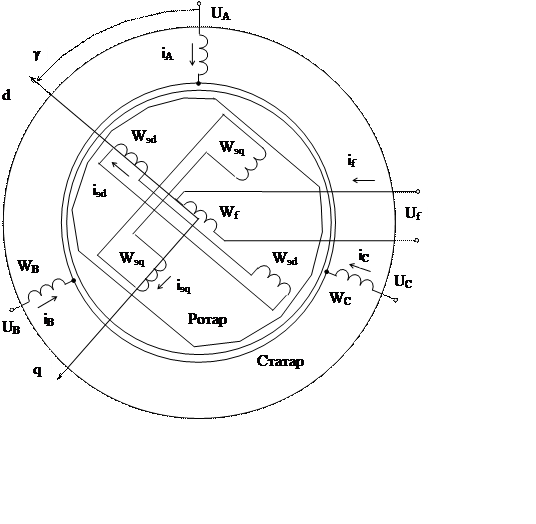Мал.1 – Cхема трохфазнай яўнаполюснай сiнхроннай машыны пры р_п=1 (р_п-колькасць пар полюсаў машыны)

2.2 Раўнанні пераходнага працэсу сінхроннай машыны

Сістэма дыферэнцыяльных раўнанняў ненасычанага сінхроннага генератара з улікам супакаяльных контураў у фізічнай сістэме каардынат мае выгляд:

Мал. 2 - Схема электрычных ланцугоў статара, ротара i нгрузкi сiнхроннага генератара: а) ў фiзiчнай сiстэме каардынатi; (б) ў сiстэме d, q каардынат.

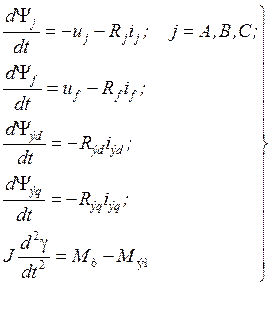                                                             (1)

дзе Ψ, u, i, R - струменесчапленне, напружанне, ток і актыўнае супраціўленне фаз А, В, С абмоткі статара;

Ψ_f, u_f, i_f, R_f - струменесчапленне, напружанне, ток і актыўнае супраціўленне абмоткі ўзбуджэння;

Ψ_эd, i_эd, R_эd, Ψ_эq, i_эq, R_эq, -  струменесчапленне, ток і актыўнае супраціўленне супакаяльных эквівалентных абмотак адпаведна па падоўжнай і папярэчнай восям;

J – момант інерцыі ротараў генератара і турбіны;

 - вугал паміж воссю d ротара і воссю фазы А статара;

M_т – механiчны момант турбiны;

М_эм - электрамагнітны момант; М_эм=1,5р_п(Ψ_di_q- Ψ_qi_d).

Усе пераменныя велічыні ў сістэме (1) выражаны ў іменаваных адзінках вымярэння.

Першыя шэсць раўнанняў сістэмы з’яўляюцца дыферэнцыяльнымі раўнаннямі першага парадку; яны адлюстроўваюць другi закон Кірхгофа для электрычных контураў машыны. Семае раўнанне з’яўляецца дыферэнцыяльным раўнаннем другога парадку – гэта раўнанне аварочвальнага руху ротара генератара i турбiны.

Дадатныя накірункі токаў у абмотках статара і ў сістэме (1) выбраны ад генератара да нагрузкі, а ў абмотцы ўзбуджэння – ад крыніцы сілкавання да абмоткі.

Першыя тры раўнанні сістэмы (1) (для абмотак статара) запісаны ў нерухомых фазных каардынатах А,В,С, а наступныя тры (для абмотак торара) - у каардынатах d, q, якія рухаюцца разам з ротарам. Такую сістэму каардынат называюць непераўтворнай, або фiзiчнай. Струменесчапленні абмотак статара і ротара ў гэтай сістэме з’яўляюцца перыядычнымі функцыямі вугла  і маюць грувасткі выгляд [1]. Таму пры мадэляванні машын, якiя маюць несіметрычны ротар, выкарыстоўваюць сістэму d, q каардынат, у якой запiсваюцца раўнаннi статара i ротара.

Пры пераходзе да d, q каардынат ланцугі ротара (мал.2) і раўнанні гэтых ланцугоў у сістэме (1) застаюцца без змянення. А трохфазная абмотка статара мадэлюецца двухфазнай абмоткай, якая рухаецца разам з восямі d, q. Ланцугі нагрузкі таксама прадстаўляцца ў восях d, q.

Выражаючы ў сістэме (1) стуменесчапленні праз токі, прымяняючы для токаў, напружанняў і струменесчапленняў формулы пераходу ад трохфазнай сiстэмы каардынат А,В,С да сiстэмы d,q, пасля ўвядзення сістэмы адносных адзiнак, атрымаем [1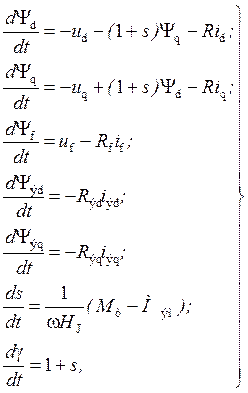,2]:

                                                                              (2)

дзе       s - слізгаценне ротара, адн. адз.; s=(ω – ω_с)/ ω_с; ω_с - сінхронная частата аварочвання поля, 1/с; ω - бягучая частата аварочвання ротара, 1/с;

H_J - пастаянная інерцыі частак агрэгата, якія аварочваюцца, с; H_J=(Jω²)/S_н;

S_н - намінальная магутнасць генератара, ВА;

М_т - механічны момант першаснага рухавіка, адн. адз.;