Динамика механических систем. Определение ускорения тел системы, направления и величины внутренних реакций

Кафедра теоретической механики

Курсовая работа по курсу «Теоретическая механика»

«Динамика механических систем»

2015

Содержание:

Введение. 3

Этап 1.     Дифференциальные уравнения движения твердого тела. 5

Этап 2.     Теорема об изменении кинетической энергии системы.. 10

Этап 3.     Принцип виртуальных (возможных) перемещений.. 14

Этап 4.     Применение общего уравнения динамики.. 16

Этап 5.     Применение уравнения Лагранжа II рода к исследованию движения системы с одной степенью свободы.. 18

Этап 6.     Применение уравнения Лагранжа II рода к исследованию движения системы с двумя степенями свободы.. 19

Заключение. 22

Список литературы.. 23

Введение

Все явления природы представляют собой движение различных форм материи. Всякое изменение материи называют движением. Одним из простейших является механическое движение − перемещение материальных объектов в пространстве с течением времени без рассмотрения физических свойств движущихся материальных объектов и их изменения в процессе движения. В теоретической механике изучают механические движения вещественных форм материальных объектов в пространстве с течением времени.

Теоретическая механика является фундаментальной дисциплиной не только для большинства общеинженерных дисциплин. Теоретические выводы механики также применяются в областях науки, в которых рассматриваются вопросы далеко немеханического происхождения, таких как электродинамика, химия, экономика и даже биология. Это связано, быть может, с тем, что теоретическая механика рассматривает фундаментальные законы природы, присущие многим объектам материи. Именно поэтому, знание основ теоретической механики, является необходимым для любого инженера, да и просто образованного человека.

Задание. Вариант  1.

Задана механическая схема, изображенная на рис. 1. Необходимо определить ускорения тел и реакции внутренних связей, используя дифференциальные уравнения движения твердого тела (этап 1).

Также необходимо определить скорость груза 1 после того как он пройдет путь  с начала движения, при условии, в начальный момент система находилась в покое (этап 2).

Используя общее уравнение динамики и уравнение Лагранжа II рода определить ускорение груза 1 (этап 4 и 5).

Необходимые для расчета данные сведены в табл. 1.

табл. 1 Исходные данные к схеме на рис. 1.

Массы тел	Радиусы колес	Коэффициент трения		Углы	Вращающий момент	Перемещение колеса 1
		качения	скольжения
, ,	,			,

Ошибка! Ошибка связи.

рис. 1 Схема механической системы.

В третьем этапе по заданной схеме необходимо определить удлинение пружины, используя принцип виртуальных (возможных) перемещений.

В шестом этапе по заданной схеме механической системы с двумя степенями свободы необходимо составить дифференциальные уравнения ее движения, используя уравнения Лагранжа II рода.

Этап 1. Дифференциальные уравнения движения твердого тела

В данной механической системе колесо 1 вращается вокруг неподвижной оси, колесо 2 совершает плоскопараллельное груз движение, а 3 совершает поступательное движение.

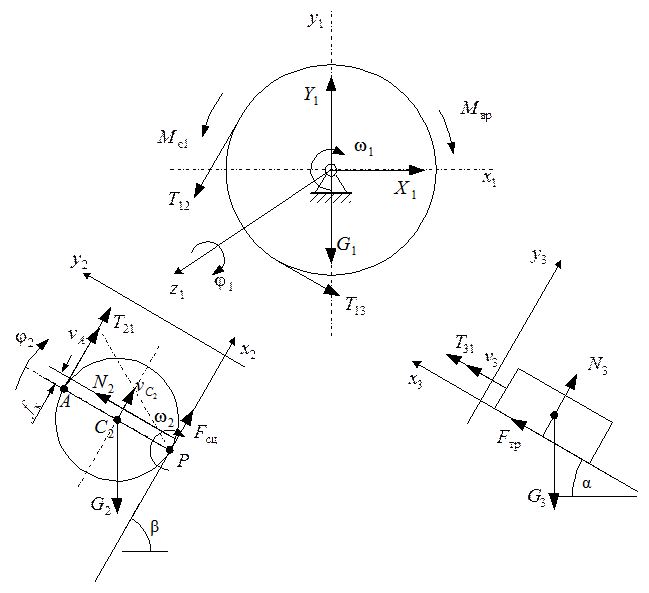
рис. 2

Напишем дифференциальные уравнения каждого из этих трех тел, для чего отделим одно от другого, разрезав нити удерживающие груз 3 и колесо 2.

К колесу 1 приложены вращающий момент , сила тяжести , момент сил сопротивления , составляющие реакции подшипника ,  и силы натяжения нитей  и .

К колесу 2 приложены сила тяжести , нормальная реакция , сила сцепления   и сила натяжения нити .

К грузу 3 приложены сила тяжести , нормальная реакция , сила трения скольжения и сила натяжения нити .

Очевидно, что

,   .                                            

Составим дифференциальное уравнение вращательного движения колеса 1 вокруг оси :

.

Здесь  - главный момент внешних сил, приложенных к колесу 1 относительно оси вращения :

.

Положительное направление угла поворота колеса 1  принято направление по часовой стрелке, что соответствует направлению вращения колеса (вращение происходит в сторону вращающего момента ). Момент сопротивление  препятствует вращение, поэтому направлен против угловой скорости .

Момент инерции колеса 1 относительно оси  равен

.                                                    

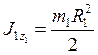Дифференциальное уравнение вращения колеса 1 примет вид

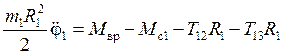, или, перенося неизвестные силы в левую часть уравнения, запишем

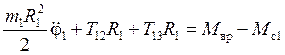.                                      (a)

Составим дифференциальные уравнения плоского движения колеса 2:

 и .[1]

Здесь  проекция главного вектора внешних сил приложенных к колесу 2 на ось ;  - главный момент внешних сил приложенных к колесу 2 относительно оси перпендикулярной плоскости рисунка и проходящей через центр масс колеса 2. Положительное направление оси  принято в сторону движения колеса 2, направление угла поворота  выбрано  по направлению часовой стрелки, что соответствует возрастанию координаты .

Проекция главный вектор внешних сил на ось  рана

.

Момент внешних сил

, где нормальную реакцию  определим из условия равновесия проекций на ось  внешних сил приложенных к колесу 2:[2]

, отсюда

.                                         

Тогда

.

Считая колесо 2 сплошным однородным диском, запишем его центральный момент инерции

.                                                    

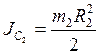Дифференциальные уравнения плоского движения колеса 2 примут вид

;