Зависимости между перемещениями имеют вид
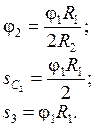
Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1, 2, 3.
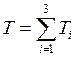 .
.
Кинетическая энергия колеса 1:
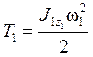 , а с учетом (1.2) и
, а с учетом (1.2) и
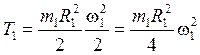 .
.
Кинетическая энергия колеса 2 сложится из кинетической энергии вращательного и поступательного движений:
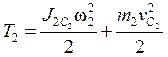 , здесь
, здесь ![]() - момент инерции колеса 2 относительно оси
перпендикулярной плоскости рисунка и проходящей через центр масс колеса 2.
учитывая (1.4) и (2.3) имеем
- момент инерции колеса 2 относительно оси
перпендикулярной плоскости рисунка и проходящей через центр масс колеса 2.
учитывая (1.4) и (2.3) имеем
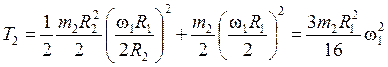 .
.
Кинетическая энергия груза поступательно движущегося 3:
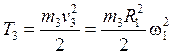 .
.
Кинетическая энергия системы определится по формуле (2.5) с учетом (2.6), (2.7) и (2.8).
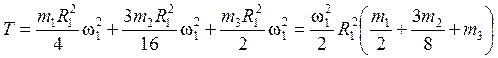 , или
, или
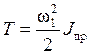 , где
, где ![]() -
приведенный к колесу 1 момент инерции системы, равный
-
приведенный к колесу 1 момент инерции системы, равный
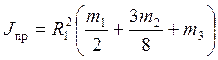 .
.
Найдем сумму работ всех внешних сил, приложенных к системе на заданном ее перемещении. Покажем внешние силы, приложенные к системе.
Работа вращающего момента приложенного к колесу 1
![]() .
.
Работа пары сил сопротивления приложенной к колесу 1
![]() .
.
Работа силы тяжести колеса 2
![]() , учитывая (2.4)
, учитывая (2.4)
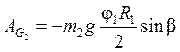 .
.
Работа пары сил сопротивления качению колеса 2
![]() , с учетом (2.4) и (1.3)
, с учетом (2.4) и (1.3)
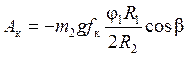 .
.
Работа силы тяжести груза 3
![]() , учитывая (2.4)
, учитывая (2.4)
![]() .
.
Работа силы трения скольжения груза 3
![]() , или с учетом (2.4) и (1.5)
, или с учетом (2.4) и (1.5)
![]()
Сумма работ внешних сил определяется сложением работ вычисляемых по формулам (2.15)-(2.16):
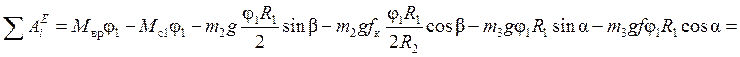
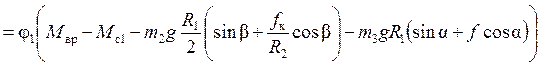 , или
, или
![]() , где
, где ![]() -
приведенный к колесу 1 момент внешних сил, равный
-
приведенный к колесу 1 момент внешних сил, равный
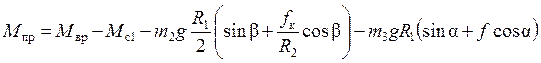 .
.
Подставляя (2.9) и (2.18) в (2.2) получим
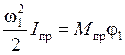 , откуда находим
, откуда находим
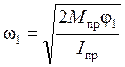 , или с учетом выражений для
, или с учетом выражений для ![]() и
и ![]() (формулы (2.10) и (2.18))
(формулы (2.10) и (2.18))
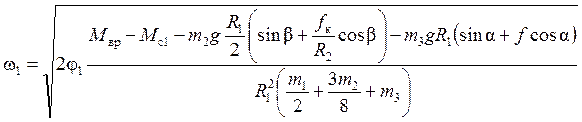 .
.
Задана механическая система (рис. 4), находящаяся в статическом равновесии. Необходимо определить деформацию
пружины![]() , применяя принцип возможных перемещений.
Необходимые исходные данные приведены в табл. 2.
, применяя принцип возможных перемещений.
Необходимые исходные данные приведены в табл. 2.
табл. 2 Исходные данные.
|
|
|
|
|
|
|
|
60 |
50 |
12 |
150 |
120 |
250 |
Ошибка! Раздел не указан.
рис. 4
Для решения задачи применим принцип виртуальных перемещений, который в случае голономной системы является принципом возможных перемещений и гласит, что сумма работ активных сил на любом возможном перемещении системы при ее равновесии равна нулю.[3]
Для того, чтобы определить
деформацию пружины необходимо определить реакцию ![]() , для
чего необходимо отбросить данную связь заменив ее действие реакцией
, для
чего необходимо отбросить данную связь заменив ее действие реакцией ![]() считая ее активной силой, сообщить системе
малое возможное перемещение и составить уравнение работ, выражающее принцип
возможных перемещений:
считая ее активной силой, сообщить системе
малое возможное перемещение и составить уравнение работ, выражающее принцип
возможных перемещений:
![]() .
.
Оставшиеся связи, наложенные на
систему, разрешают следующие возможные перемещения: поворот кривошипов ![]() и
и ![]() вокруг
неподвижных точек
вокруг
неподвижных точек ![]() и
и ![]() соответственно,
перемещение точек
соответственно,
перемещение точек ![]() ,
, ![]() и
и ![]() на
на ![]() ,
, ![]() и
и ![]() соответственно
и поворот треугольника
соответственно
и поворот треугольника ![]() на угол
на угол ![]() .
.
Замечая, что ![]() ,
, ![]() и
и ![]() (здесь
точка
(здесь
точка ![]() – мгновенный центр перемещений тела
– мгновенный центр перемещений тела ![]() ) запишем уравнение работ для заданной
системы.
) запишем уравнение работ для заданной
системы.
![]() , где
, где ![]() − сила упругости пружины,
равная
− сила упругости пружины,
равная
![]() .
.
Выразим все возможные
перемещения, через возможное перемещение ![]() .[4]
.[4]
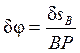 , расстояние
, расстояние ![]() определим из
определим из ![]() :
:
![]() , но
, но ![]() , так как
, так как ![]() –
прямоугольный и
–
прямоугольный и ![]() , тогда
, тогда
![]() ,
,
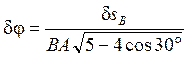 .
.
Возможное перемещение ![]() выразится следующим образом:
выразится следующим образом:
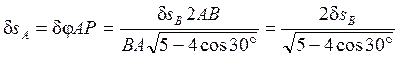 .
.
Возможное перемещение ![]()
![]() , где
, где ![]() , тогда
, тогда
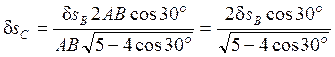 .
.
Определим ![]() .
.
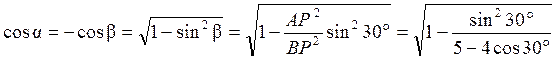
Подставляя (3.2) – (3.6) в (3.1), получим следующее уравнение
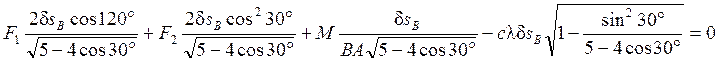 , откуда находим
, откуда находим
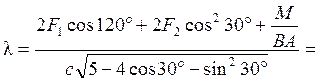 32,8
см.
32,8
см.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.