Динамика механических систем. Определение ускорения тел системы, направления и величины внутренних реакций, страница 5

Здесь ─ кинетическая энергия системы, соответствующая состоянию системы, характеризуемого обобщенными координатами  и  и обобщенными скоростями  и ; – потенциальная энергия системы;  и   ─ обобщенные силы, соответствующие не консервативным силам.

Кинетическую энергию системы найдем как сумму кинетических энергий тел входящих в нее:

.                                                 

Выразим скорости центров масс и угловые скорости твердых тел системы через обобщенные скорости.

Скорость тела 2 движущегося поступательно

.                                                         

Скорость материальной точки 1

, где  – относительная скорость точки, равная

;

 – переносная скорость точки, равная

.

Модуль вектора  равен

.               

Скорость центра масс колеса 3 точки  равна

,                                                     а его угловая скорость равна

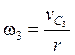,                                                        где  – радиус колеса.

Момент инерции колеса 3 относительно центральной оси

.                                                                                                                                                                                                    

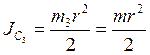С учетом (6.4) – (6.8) кинетические энергии тел раны:

;                                      

;                                             

.                      

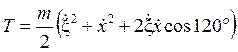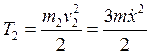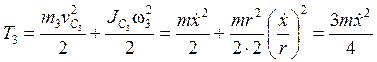Подставляя  (6.9), (6.10)  и (6.11) в (6.3) получим

.                                                                        

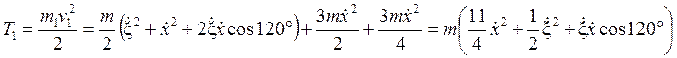Потенциальную энергию системы определим, как работу сил тяжести материальной точки 1 при ее перемещении из данного положения, характеризуемого обобщенной координатой  в некоторое исходное, например, то от которого ведется отсчет обобщенной координаты . [7]

.                                    

Обобщенные силы определим из выражений мощности неконсервативных сил на возможных скоростях системы, соответствующих возрастанию каждой обобщенной координаты

.                                            

.                         

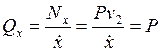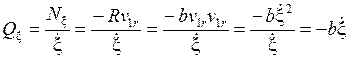Здесь – сила вязкого сопротивления.

Подставляя (6.12) – (6.15) в (6.1) и (6.2) получим

;

.

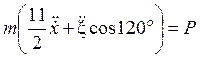Заключение

В результате проведенной работы были определены ускорения тел системы, направления и величины внутренних реакций. Определена угловая скорость колеса 1 по прошествии им заданного угла поворота от начала движения системы. Ускорение груза 1 было определено также при помощи основного уравнения динамики и уравнения Лагранжа.

В третьем этапе по заданной схеме механической системы, находящейся в статическом равновесии, определена деформация пружины.

В шестом этапе по заданной схеме механической системы с двумя степенями свободы, найдены дифференциальные уравнения ее движения.

Список литературы

1.  Н.Н. Никитин, «Курс теоретической механики», М.: ВШ, 1990.

2.  А.А. Яблонский, «Сборник заданий для курсовых робот по теоретической механике», М.: ВШ, 1985.

3.  Ф.Р. Гантмахер, «Лекции по аналитической механике», М.: Физматлит, 2001.