Если связи системы идеальны и удерживающие, то для исследования движения механической системы можно применить общее уравнение динамики.
В заданной механической системе плоскости, по которым движутся груз 3 и колесо 2 не являются удерживающими связями, но все время движения эти тела не отрываются отрыва от плоскостей, поэтому данные связи заменяются двусторонними.
Так как плоскость, по которой движется груз 3, является шероховатой (неидеальная связь), то необходимо заменить ее гладкой плоскостью и активной силой трения скольжения.
Неидеальную связь - плоскость, по которой катится колесо 2, также заменяем идеальной плоскостью[5] и активной силой сопротивления качению.
Таким образом, к рассматриваемой механической системе можно применить общее уравнение динамики.
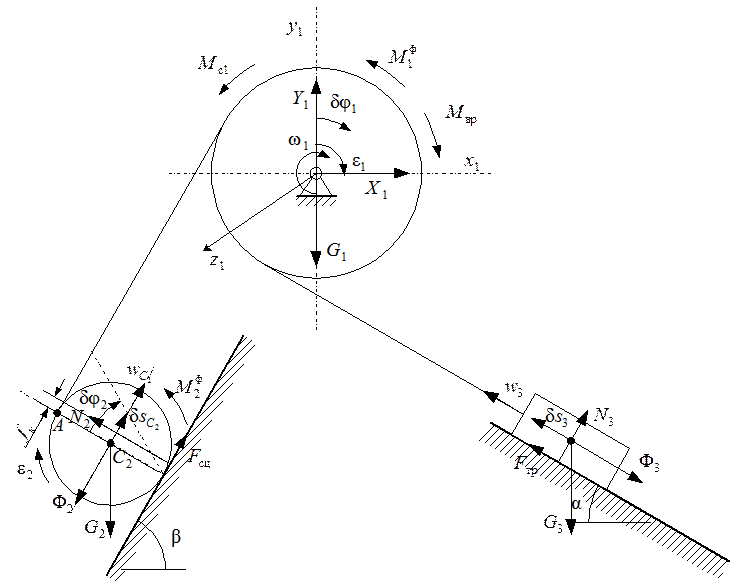
рис. 5
Запишем общее уравнение динамики для заданной механической системы.
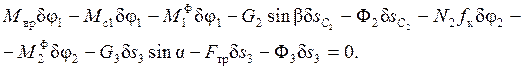
Зависимости между возможными перемещениями будут такими же, как и между возможными скоростями, а так как действительные скорости являются одной из реализаций возможных скоростей, то зависимости между возможными перемещениями будут такими же, как и между действительными скоростями. Таким образом, запишем (см (2.3))
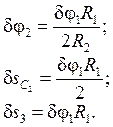
Дифференцируя (2.3) по времени получим зависимости между ускорениями тел
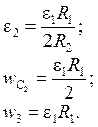
Силы инерции тел:
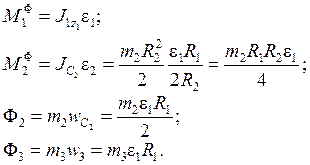
С учетом (4.2), (4.3), (1.3) и (1.5) уравнение (4.1) принимает вид.
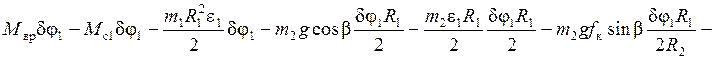
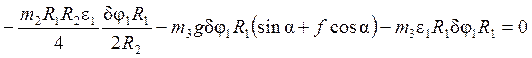 , отсюда находим
, отсюда находим
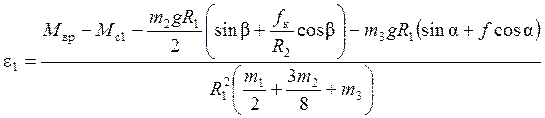 .
.
При исследовании движения голономных склерономных систем с идеальными связями[6] (сумма работ реакций связей на любом возможном перемещении системы равна нулю), возможно применение уравнений Лагранжа II рода.
Поскольку система имеет одну степень свободы то количество дифференциальных уравнений равно единице.
Так как необходимо найти угловое
ускорение колеса 1, то в качестве обобщенной координаты удобно принять
угол поворота ![]() колеса 1 относительно
неподвижной оси
колеса 1 относительно
неподвижной оси ![]() .
.
Запишем уравнение Лагранжа II рода в следующем виде
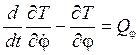 , где
, где ![]() ─ кинетическая энергия системы;
─ кинетическая энергия системы; ![]() ─ обобщенная сила, соответствующая всем
активным силам.
─ обобщенная сила, соответствующая всем
активным силам.
Согласно выражению для
кинетической энергии системы (формула (2.9)) и учитывая, что ![]() , имеем.
, имеем.
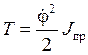 .
.
Обобщенную силу можно определить из выражений роботы внешних сил на возможном перемещении системы.
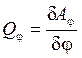 .
.
Согласно (2.17) имеем
![]() , тогда
, тогда
![]() .
.
Подставим (5.2) и (5.3) в (5.1) и замечая, что приведенный момент инерции системы ![]() не
зависит ни от обобщенной скорости, ни от обобщенной координаты, ни от времени,
получим
не
зависит ни от обобщенной скорости, ни от обобщенной координаты, ни от времени,
получим
![]() , откуда находим
, откуда находим
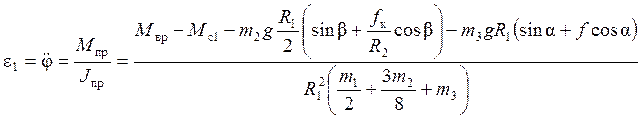 .
.
Найти уравнение движения системы
в обобщенных координатах ![]() и
и ![]() при заданных начальных условиях.
Необходимые данные приведены в табл. 3; там же указаны рекомендуемые обобщенные
координаты.
при заданных начальных условиях.
Необходимые данные приведены в табл. 3; там же указаны рекомендуемые обобщенные
координаты.
табл. 3
|
Номер варианта из Д21, «Яблонский» |
Массы тел |
Радиусы инерций |
Силы |
Моменты |
Коэффициенты |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
|
|
трения скольжения |
вязкого сопротивления |
||||||||
|
24 |
|
|
|
– |
– |
– |
– |
|
– |
– |
|
|||||
|
Обобщенные координаты |
Начальные условия |
Дополнительные данные |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
0 |
0 |
1 – материальная точка |
||||||||||
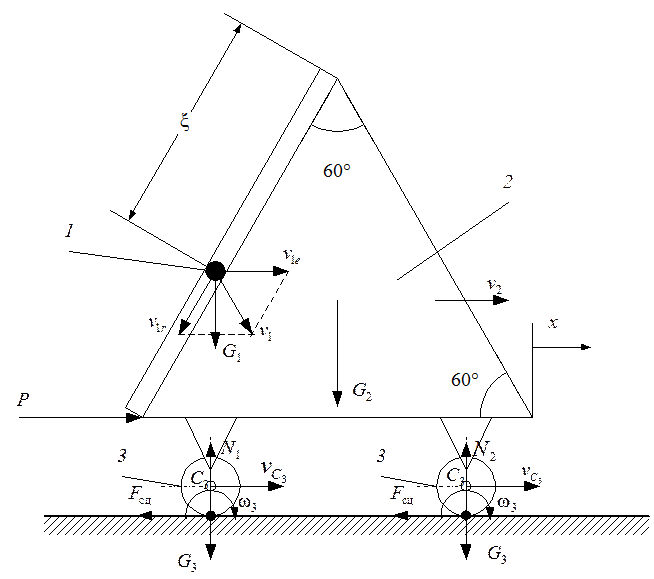
рис. 6
Для решения задачи применим уравнения Лагранжа II рода.
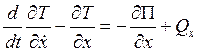 ;
;
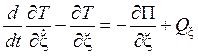 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.