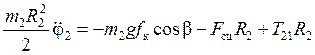 , или перенося неизвестные слагаемые в левую часть уравнений
, или перенося неизвестные слагаемые в левую часть уравнений
![]() ; (b)
; (b)
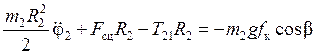 . (c)
. (c)
Составим дифференциальное уравнение поступательного движения груза 3:
![]() и
и ![]() .
.
Здесь ![]() и
и ![]() проекции главного вектора внешних сил
приложенных к грузу 3 на оси
проекции главного вектора внешних сил
приложенных к грузу 3 на оси ![]() и
и ![]() соответственно. Положительное направление
оси
соответственно. Положительное направление
оси ![]() принято в сторону движения груза 3,
направление оси
принято в сторону движения груза 3,
направление оси ![]() значение не имеет, поскольку
вдоль нее движения груза не происходит, а это значит, что
значение не имеет, поскольку
вдоль нее движения груза не происходит, а это значит, что
![]() .
.
Из полученного уравнения равновесия находим
![]() .
.
Проекция главного вектора внешних
сил на ось ![]() рана
рана
![]() , где сила трения скольжения определится по формуле
, где сила трения скольжения определится по формуле
![]() .
.
Таким образом, запишем полученное дифференциальное уравнение поступательного движения груза 3:
![]() , или
, или
![]() . (d)
. (d)
К полученным четырем уравнениям ((a)– (d) ) добавим уравнения связей.
Поскольку нить, соединяющая груз 3
и обод колеса 1 нерастяжима и все время движения параллельна оси ![]() , то можно записать следующее уравнение
связей
, то можно записать следующее уравнение
связей
![]() , или
, или ![]() .
.
Дифференцируя (1.6) по времени получим
![]() , или
, или
![]() . (e)
. (e)
Нить, соединяющая колеса 1
и 2 нерастяжима и все время движения параллельна оси ![]() , а также колесо 2 катится без
проскальзывания, следовательно
, а также колесо 2 катится без
проскальзывания, следовательно
![]() , или
, или
![]() ;
;
![]() .
.
Дифференцируя (1.7) и (1.8) по времени получим
![]() ; (f)
; (f)
![]() . (g)
. (g)
Таким образом, с учетом (1.1) получена нормальная система линейных уравнений (a)–(g) относительно ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
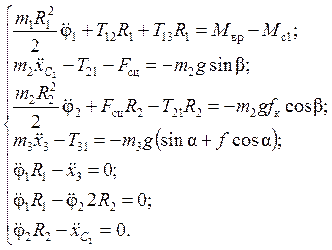
Решим полученную систему линейных
уравнений (1.9), для чего выразим из трех последних уравнений ![]() ,
, ![]() и
и ![]() через
через ![]() :
:
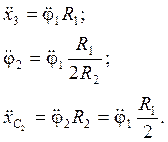
Подставим полученные выражения
для ![]() ,
, ![]() и
и ![]() во второе третье и четвертое уравнения
системы (1.9), после чего порядок системы уменьшится на 3 и будем иметь
следующую систему линейных уравнений 4-го порядка:
во второе третье и четвертое уравнения
системы (1.9), после чего порядок системы уменьшится на 3 и будем иметь
следующую систему линейных уравнений 4-го порядка:
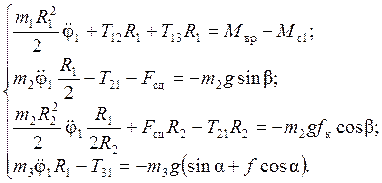
Умножая второе уравнение системы (1.11) на ![]() и складывая его с третьим, получим
следующую систему 3-го порядка
и складывая его с третьим, получим
следующую систему 3-го порядка
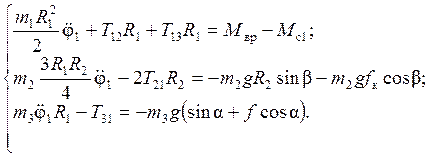
Теперь, умножая второе уравнение
системы (1.12) на ![]() , а третье - на
, а третье - на ![]() и
складывая все три уравнения системы будем иметь следующее уравнение
и
складывая все три уравнения системы будем иметь следующее уравнение
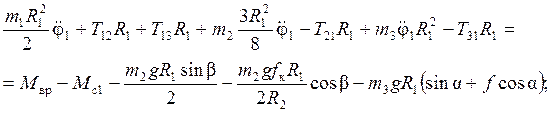
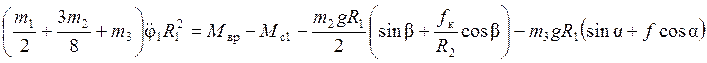 , откуда
, откуда
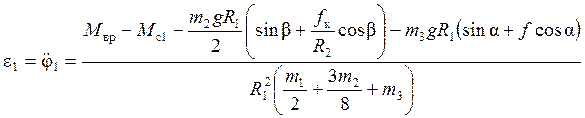 .
.
Таким образом, найдено угловое ускорение колеса 1.
Необходимо определить угловую
скорость ![]() колеса 1 в положении, когда оно
повернется на угол
колеса 1 в положении, когда оно
повернется на угол ![]() от начла движения. В начальный
момент времени система покоилась.
от начла движения. В начальный
момент времени система покоилась.
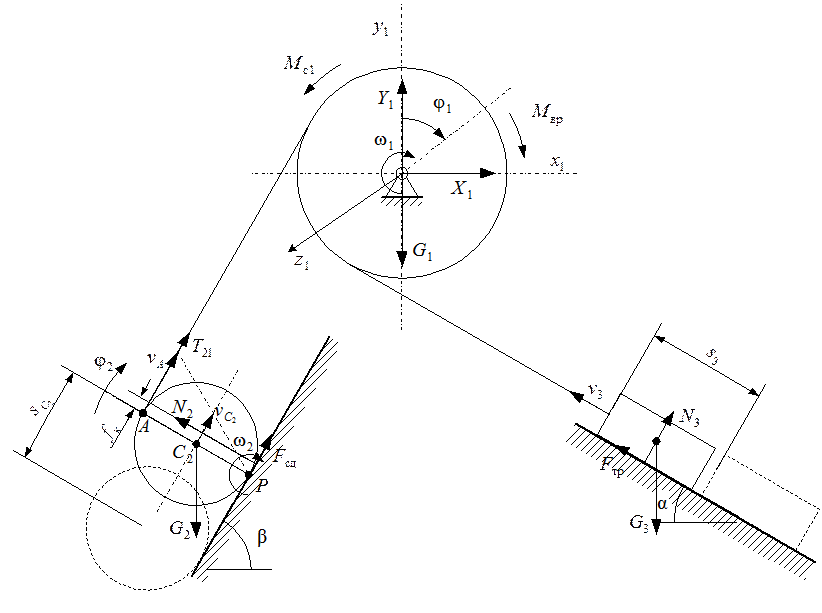 рис. 3
рис. 3
Для определения скорости колеса 1 применим теорему об изменении кинетической энергии механической системы
![]() , где
, где ![]() и
и ![]() ─
кинетическая энергия системы в начальном и конечном положениях;
─
кинетическая энергия системы в начальном и конечном положениях; ![]() ─ сумма работ внешних сил, приложенных к
системе на перемещении системы из начального положения в конечное;
─ сумма работ внешних сил, приложенных к
системе на перемещении системы из начального положения в конечное; ![]() ─ сумма работ внутренних сил системы на
том же перемещении.
─ сумма работ внутренних сил системы на
том же перемещении.
Поскольку в начальный момент времени система покоилась, то
![]() .
.
Внутренние связи системы идеальны (нити нерастяжимы, тела абсолютно твердые), следовательно
![]() .
.
Тогда (2.1) принимает вид:
![]() .
.
Для определения кинетической
энергии ![]() и суммы работ внешних сил надо изобразить
систему в конечном положении.
и суммы работ внешних сил надо изобразить
систему в конечном положении.
Запишем зависимости между скоростями и перемещениями тел системы, т. е. уравнения связей, при этом скорости и перемещения выразим соответственно через скорость и перемещение колеса 1.
Угловая скорость колеса 2 выразится следующим образом
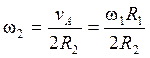 , а скорость го центра масс точки
, а скорость го центра масс точки ![]()
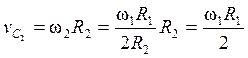 .
.
Скорость груза 3
![]() ,
,
Таким образом, получены следующие кинематические соотношения между скоростями тел системы
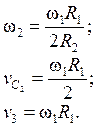
Зависимости между перемещениями тел можно получить интегрированием соотношений (2.3) по времени
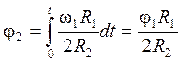 ;
;
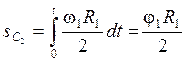 ;
;
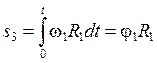 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.