Санкт-Петербургский государственный технологический институт
(технический университет)
“Определение реакций опор составной конструкции”.
Вариант №2 Срок сдачи: ___________
Выполнил: ст. *.
Проверил: преп. Иванов Ю. А.
Санкт-Петербург
2003 г.
Исходные данные.
Схема конструкции.
|
P1, кН |
P2, кН |
M0, кНм |
q, кН/м. |
|
10 |
14 |
12 |
1 |
Найти.
По заданным значениям сил, действующих на конструкцию определить реакции опор, а также соединения С.
Решение.
1. Рассмотрим систему уравновешивающих сил, приложенных к правой части составной конструкции. Согласно аксиомам статики имеем, что:
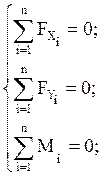
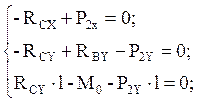
Из первого уравнения системы получаем, что
RCX=P2X=P2∙cos30º=14∙0.866=12.12 кН.
Из уравнения моментов относительно точки B имеем:
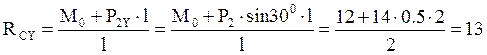 кН.
кН.
Из второго уравнения системы найдём проекцию реакции опоры B на ось ординат.
RBY= RCY+P2Y = RCY+P2∙sin30º=13+14∙0.5=20 кН.
2. Рассмотрим систему уравновешивающих сил, приложенных к левой части составной конструкции. Согласно аксиомам статики имеем, что:
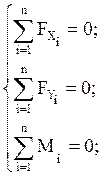
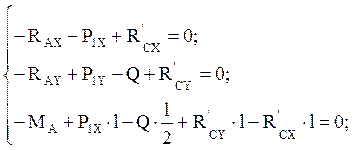
где Q=q∙l=1∙2=2 кН - сосредоточенная нагрузка, а ![]() ,
, ![]() .
.
Найдём из первого уравнения проекцию реакции опоры в точке A на ось абсцисс.
RAX=![]() -P1X=
-P1X=![]() -P1∙cos45º=12.12-10∙0.707=5.05 кН.
-P1∙cos45º=12.12-10∙0.707=5.05 кН.
Из второго уравнения системы имеем, что проекция реакции опоры на ось ординат в точке A равна:
RAY=P1Y-Q+![]() =P1∙sin45º-Q+
=P1∙sin45º-Q+![]() =10∙0.707-2+13=18.07 кН.
=10∙0.707-2+13=18.07 кН.
Согласно нашим вычислениям, модуль реакции опоры в точке A при шарнирном соединении в точке C равен:
![]() Кн.
Кн.
Момент заделки найдём из уравнения моментов сил относительно точки A.
MA=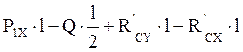
MA=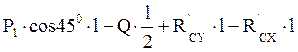 =10∙0.707∙2–2+13∙2–12.12∙2=13.9
кНм.
=10∙0.707∙2–2+13∙2–12.12∙2=13.9
кНм.
Результаты расчётов.
|
RAX, кН |
RAY, кН |
R, кН |
RB, кН |
RCX, кН |
RCY, кН |
MA, кНм |
|
5.05 |
18.07 |
18.76 |
20 |
12.12 |
13 |
13.9 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.