Типовые задачи теоретической механики
Теоретическая механика изучает в наиболее общем виде вопросы нахождения механических примитивов (материальных точек, стержней (отрезков), материальных тел (цилиндров и др.)) в состоянии покоя (равновесия – статика) и в состоянии движения (прямолинейного и (или) вращательного);
При рассмотрении задач статики – нас интересуют реакции в опорах (подвижных и неподвижных) ,заделках;
При рассмотрении вопросов динамики – нас интересуют линейная скорость и ускорение, угловая скорость и ускорение.
Геометрические преобразования, используемые в теоретической механике – прямолинейное (криволинейное – по траектории кривой) перемещение, вращение вокруг центра вращения (мгновенного центра вращения (ускорения).
Теорема Виллиса – использует рассмотрение движения (как правило, вращательного) в разных (локальных системах координат).
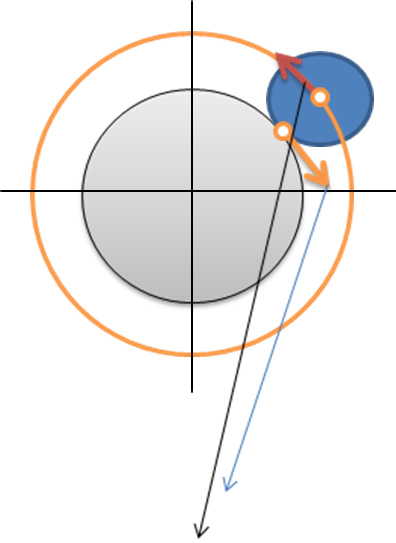 |
 Рис.1. Вращение шестерёнки в составе редуктора
Рис.1. Вращение шестерёнки в составе редуктора
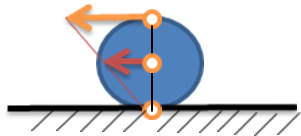 |
Рис.2. Шестеренка в системе координат МЦС (теорема Виллиса).
Базовые соотношения:
V = ω*R
ɛ =
Линейное ускорение - a
а = SQR ( aвр2 + aос2 )
aвр =
aос =
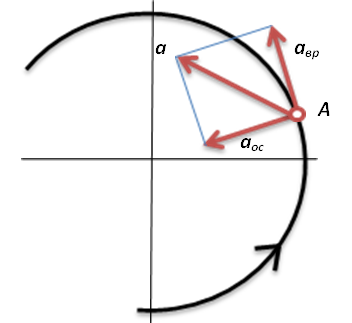 |
Рис.3. Полное ускорение точки
Мгновенная скорость (вектор) – первая производная пути по времени.
Мгновенное ускорение (вектор) – вторая производная пути по времени.
Материальные тела в ТМ часто находятся в нескольких движениях одновременно. Особенно это характерно для редукторов, в которых паразитные колеса вращаются относительно собственной оси и относительно осей входного (выходного) валов.
В статике используется система уравнений для сил и моментов в проекциях на оси координат.
В динамике используется теорема Виллиса для эквивалентного пересчета скоростей и ускорений точек материальных тел. В сложных движениях используется понятие МЦС (мгновенного центра скоростей ( ускорений)) ( см. рис.2 )
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.