19. Какую аэродинамическую силу вы определили в эксперименте?
20. Почему возникает подъемная сила?
21. Как предотвратить срыв потока?
22. Укажите точку на профиле, в которой местное число Маха потока может достигнуть значения М = 1 при a = const?
Лабораторная работа № 3
ОПРЕДЕЛЕНИЕ АЭРОДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК МОДЕЛЕЙ
ПРИ ПОМОЩИ ТЕНЗОМЕТРИЧЕСКИХ ВЕСОВ
Цель работы
1. Изучить устройство и принцип действия аэродинамических тензовесов.
2. Изучить методику проведения весовых испытаний.
3. Экспериментально определить аэродинамические характеристики модели крыла.
Введение
Весовые испытания заключаются в определении при помощи аэродинамических весов силового взаимодействия потока с моделью и нахождении ее аэродинамических характеристик. Весовые испытания – важнейший вид аэродинамического эксперимента, обязательно предшествующий созданию летательных аппаратов (ЛА).
Современная аппаратура для проведения испытаний представляет собой сложный измерительный комплекс, включающий вычислительную машину (ЭВМ), которая управляет экспериментом по заданной программе, проводит сбор и обработку экспериментальных данных. Важнейшим звеном измерительной аппаратуры являются аэродинамические весы.
Аэродинамическую нагрузку, действующую на ЛА принято представлять при помощи проекций результирующей аэродинамической силы и момента на оси соответствующей системы координат. Таким образом, задачей весового эксперимента является определение трех проекций результирующей аэродинамической силы и трех проекций результирующего момента, т.е. в общем случае весы должны быть шестикомпонентными. Если модель симметрична и угол скольжения равен нулю (случай продольного движения), то достаточно измерить три компонента: две силы (нормальную – Y и продольную – Х) и один момент (продольный – Mz). В этом случае достаточно иметь трехкомпонентные весы. Если необходимо определить, например, только силу лобового сопротивления, то достаточно однокомпонентных весов.
Аэродинамические весы подразделяются на два основных типа: механические и тензометрические. Тензовесы могут быть как встроенными в модель, так и расположенными вне модели.
Механические весы по сравнению с тензовесами имеют большую точность и стабильность (относительная погрешность измерений менее 0,02 % от измеряемой величины), однако более громоздки, сложны и дорогостоящи. К тому же их большая инерционность не позволяет исследовать быстропротекающие и нестационарные процессы.
Современные тензовесы, немногим уступающие в точности механическим весам, более удобны в эксплуатации, отвечают требованиям автоматизации эксперимента, позволяют проводить измерения при быстропротекающих (Dt < 10–3 с) процессах и поэтому находят все большее применение в практике аэродинамического эксперимента.
Аэродинамические трехкомпонентные тензовесы
В данной работе применяются трехкомпонентные тензометрические весы, расположенные вне модели. Общий вид весов с установленной на них моделью показан на рис. 3.1. На рисунке обозначены: 1 – модель, 2 – державка, 3 – тензовесы, закрытые обтекателем, 4 – «сабля» альфа-механизма.
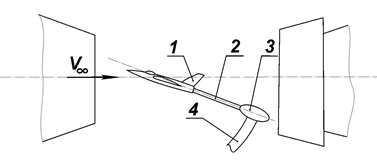
Рис. 3.1
Механическая часть
конструкции весов представляет собой совокупность упругих и относительно
жестких элементов. На упругие элементы наклеены тензодатчики, т.е электрические
сопротивления, величина которых меняется при деформациях. В рассматриваемых
весах применены кремниевые тензорезисторы с номинальным сопротивлением R= 200 Ом, имеющие длину 3 мм, ширину
0,2 мм и толщину
0,1 мм. Коэффициент тензочувствительности датчиков S» 100.
Принцип действия тензовесов следующий: под действием нагрузок, приложенных к весам, упругие элементы деформируются; тензодатчики, деформируясь вместе с упругими элементами, изменяют свое сопротивление (увеличивают при растяжении и уменьшают при сжатии); измерительная аппаратура по изменению сопротивления тензодатчиков позволяет определить деформации упругих элементов, а зная величину деформаций, можно определить нагрузки, действующие на модель.
Следует отметить, что
изменение сопротивления тензодатчиков DR довольно мало, так при максимально допустимой для
тензовесов деформации 
(s » 1000 кг/см2 для стали) и номинальном сопротивлении
R= 200 Ом у проволочных тензодатчиков DRmax » 0.2 Ом,
у кремниевых DRmax» 10 Ом. Приемлемая степень точности
при измерении таких малых относительных изменений сопротивления может быть
получена лишь при мостовой схеме измерений.
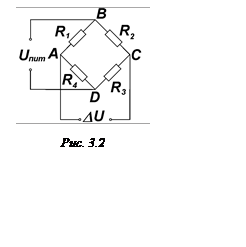Измерительный мост (мост Уитстона) в простейшем
варианте состоит из четырех сопротивлений (плеч моста) (рис. 3.2). К точкам В
и D (диагональ питания) подводится
напряжение питания (в данной работе постоянное напряжение Uпит £ 2 В). Точки А, С
(диагональ измерения) соединяются с фиксирующим прибором. В тензовесах обычно
датчики включаются во все четыре плеча моста.
Если произведения сопротивлений в противоположных плечах моста равны между собой, т.е.
, (3.1)
то разность потенциалов на диагонали моста равна нулю – мост уравновешен (сбалансирован). При изменении одного или нескольких сопротивлений между точками А и С появляется разность потенциалов DU = Uвых (напряжение разбаланса), которая при малых DR/R линейно зависит от суммы или разности изменений сопротивления.
Для получения максимально возможного напряжения разбаланса необходимо, чтобы в правой и левой частях уравнения (3.1) изменения сопротивлений были противоположного знака. Таким образом, для получения максимально возможной чувствительности тензодатчики, испытывающие одноименные деформации, должны включаться во взаимно противоположные плечи моста, при этом в смежных плечах окажутся датчики с деформациями противоположных знаков.
Аэродинамические весы предназначены для определения проекций сил и моментов на оси координат при произвольном направлении сил и моментов, действующих на модель. Решение этой задачи (разделение компонентов) возможно механическим и (или) электрическим способом. Под механическим способом подразумевается выбор геометрической формы весов таким образом, чтобы деформация в каждом упругом элементе, вызываемая измеряемым компонентом, существенно превышала деформации, порожденные другими компонентами.
Электрический способ разделения
компонентов заключается в выборе такой схемы наклейки датчиков и соединения их
в мост, при которой изменения сопротивлений, обусловленные измеряемым компонентом,
происходят во взаимно противоположных плечах моста, вызывая его разбаланс: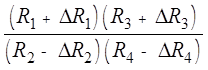 
, а изменения сопротивлений от прочих
компонентов –не создают напряжения разбаланса, например: 
.
Обычно 
.Проиллюстрировать это можно так
(рис. 3.3): из трех групп датчиков, наклеенных на одну и ту же консольную
балочку и соединенных определенным образом в мосты, одна фиксирует сигнал,
пропорциональный компоненту Х (рис. 3.3, а), другая –
пропорциональный моменту Мx (рис. 3.3, б), третья –
моменту Mz относительно места наклейки датчиков R9 – R12 (рис. 3.3, в).
В тензовесах, используемых в настоящей работе (рис. 3.4), разделение компонентов происходит в основном механическим способом, кроме того, места наклейки тензодатчиков выбраны таким образом, чтобы дополнительно обеспечивалось электрическое разделение компонентов.
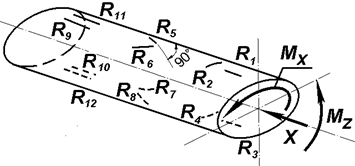
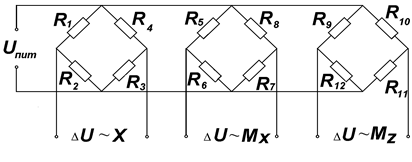
а б в
Рис. 3.3
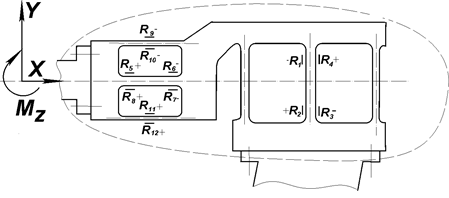
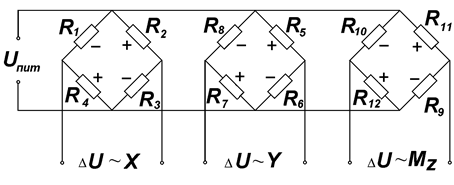
В конструкции весов можно выделить два упругих параллелограмма, в середине которых имеются более жесткие, чем по краям, упругие элементы.
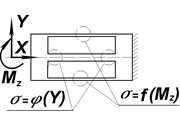
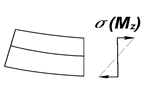
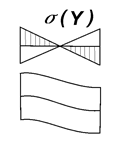
Рассмотрим работу первого по потоку параллелограмма. Со стороны державки на элемент действуют продольная сила Х, нормальная сила Y и продольный изгибающий момент Mz (рис. 3.5, а). Момент Mz вызывает чистый изгиб параллелограмма (рис. 3.5, б). Так как средняя балочка расположена на нейтральной оси, то момент практически полностью воспринимается крайними балочками, одна из которых испытывает деформацию растяжения, другая – сжатия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
