Лекция1
Основы теории линейных импульсных (цифровых) систем управления.
 Импульсные системы автоматического
регулирования (их называют также иногда системами прерывистого регулирования)
представляют собой особый класс систем, которые в ряде случаев могут быть
описаны с помощью линейных уравнений. В этих системах определение
рассогласования (ошибки) между заданной и регулируемой величинами производится
не непрерывно, а лишь в дискретные моменты времени, называемые моментами
съема, разделенные, как правило, одинаковыми интервалами времени. Внутри этих
интервалов управление движением системы регулирования производится в
соответствии с ранее измеренными дискретными значениями рассогласования.
Теория импульсных систем автоматического регулирования разрабатывалась Я. 3.
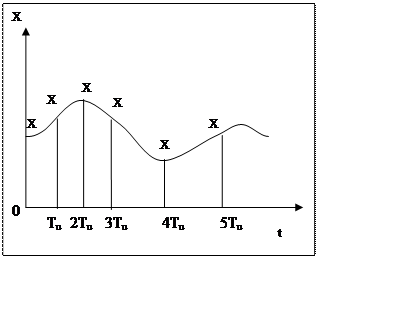
Цыпкиным. Представление сигнала с помощью дискретных его значений как это
показано на рис. 12.1,а, называют Рис. 12.1 иногда квантованием по времени. В
импульсных системах автоматического регулирования квантованный по времени
сигнал рассогласования модулирует последовательность управляющих импульсов. При
этом форма импульсов может быть произвольной и, в принципе, может быть
использован любой из известных видов модуляции: амплитудная, широтная,
фазовая, частотна.
Импульсные системы автоматического
регулирования (их называют также иногда системами прерывистого регулирования)
представляют собой особый класс систем, которые в ряде случаев могут быть
описаны с помощью линейных уравнений. В этих системах определение
рассогласования (ошибки) между заданной и регулируемой величинами производится
не непрерывно, а лишь в дискретные моменты времени, называемые моментами
съема, разделенные, как правило, одинаковыми интервалами времени. Внутри этих
интервалов управление движением системы регулирования производится в
соответствии с ранее измеренными дискретными значениями рассогласования.
Теория импульсных систем автоматического регулирования разрабатывалась Я. 3.
Цыпкиным. Представление сигнала с помощью дискретных его значений как это
показано на рис. 12.1,а, называют Рис. 12.1 иногда квантованием по времени. В
импульсных системах автоматического регулирования квантованный по времени
сигнал рассогласования модулирует последовательность управляющих импульсов. При
этом форма импульсов может быть произвольной и, в принципе, может быть
использован любой из известных видов модуляции: амплитудная, широтная,
фазовая, частотна.
Принцип импульсного регулирования получил применение в системах автоматического регулирования с цифровыми вычислительными устройствами, в многоканальных системах автоматического регулирования, в радиолокационных устройствах и в некоторых других системах.
Лекция2
- АЦП – аналого-цифровой преобразователь.
Фиксация в определенный момент времени какой-либо величина.
То -такт, период дискретизации
- Импульсный элемент.
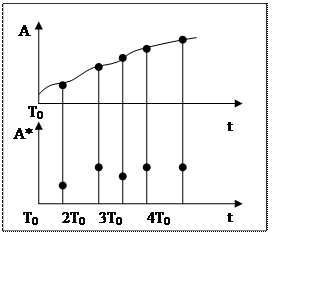
|
A→ → А*
-
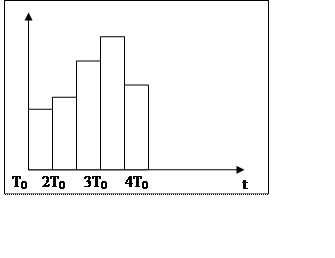
 фиксатор (экстраполятор) нулевого порядка ФНП (ЭНП).
фиксатор (экстраполятор) нулевого порядка ФНП (ЭНП).
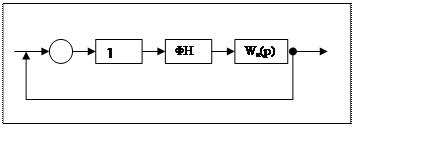
Расчетная структурная схема импульсной системы.

|
![]()
![]()
![]()

![]()
![]() [к.т.]
[к.т.]
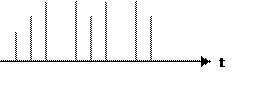 |
в промежуточный момент времени сигнал отсутствует.
∆А* - первая разность.
![]() разность
между последующим текущим моментом.
разность
между последующим текущим моментом.
![]() вторая
разность (вторая производная).
вторая
разность (вторая производная).
![]()
Разностное уравнение – аналог дифференциальному.
Дискретное преобразование Лапласа или z преобразование.
Позволяет работать с дискретными аналогами.
(сдвиг влево)![]() оператор
сдвига (по времени вправо влево)
оператор
сдвига (по времени вправо влево)
![]() - вправо
задержка по времени.
- вправо
задержка по времени.
Важной особенностью спектра дискретного сигнала
является его периодичность по оси частот с периодом 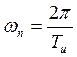 :
:
![]()
|
|
|
|
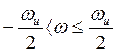 для других частот картина будет
периодически повторяться. Эта полоса может быть сужена вдвое
для других частот картина будет
периодически повторяться. Эта полоса может быть сужена вдвое 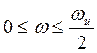 , если учесть общее для всех спектров свойство,
согласно которому значение спектра для отрицательной частоты может быть
получено из значения спектра для той же (по абсолютной величине) положительной
частоты путем сопряжения.
, если учесть общее для всех спектров свойство,
согласно которому значение спектра для отрицательной частоты может быть
получено из значения спектра для той же (по абсолютной величине) положительной
частоты путем сопряжения.
 Изображение Х*(р) также периодично в плоскости
р вдоль мнимой оси с периодом
Изображение Х*(р) также периодично в плоскости
р вдоль мнимой оси с периодом ![]() . Поэтому при рассмотрении изображений Х*(р)
можно ограничиться горизонтальной полосой с шириной wи, симметрично
расположенной, относительно действительной оси (рис. 12.14),
. Поэтому при рассмотрении изображений Х*(р)
можно ограничиться горизонтальной полосой с шириной wи, симметрично
расположенной, относительно действительной оси (рис. 12.14),
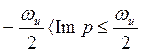 (12.14)
(12.14)
Лекция3
Свойства z-преобразования.
1. св – во: линейность преобразований.
![]()
2. Сдвиг по времени вправо:
![]()
3. Сдвиг по времени влево:
|
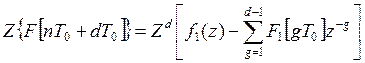
4.
Начальное
значение функции: ![]()
5. Конечное значение:
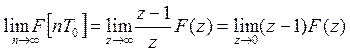
Таблица z – преобразований элементарных функций:
|
F(T) |
F(p) |
F(z) |
|
1 |
1/p |
z/z-1 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная передаточная функция
Отношение выходного сигнала к входному, записанные в дискретные значения времени.
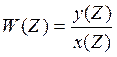
 |
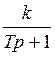 W(z)
W(z)
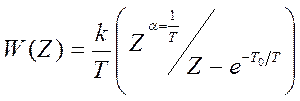
Лекция4
![]()
![]()
|
|
|
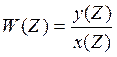
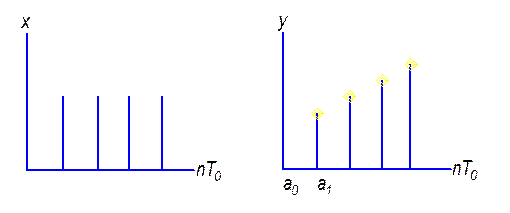

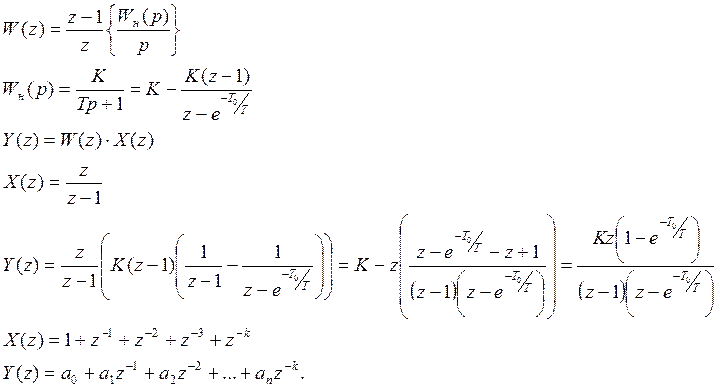
Ряд Лорана.
Свойство передаточных функций
1. Статический коэффициент передачи, получаемый с дискретной передаточной функцией соответствует конечному значению функции.
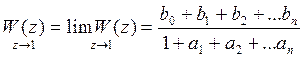
2. Передаточная функция систем запаздывания характерна тем, что в ней имеется множитель явно выраженный
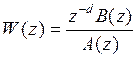
3. Дискретная передаточная функция реализуема, если полином числителя равен или меньше полинома знаменателя.
4. В статических системах с астатизмом e
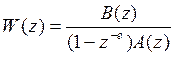
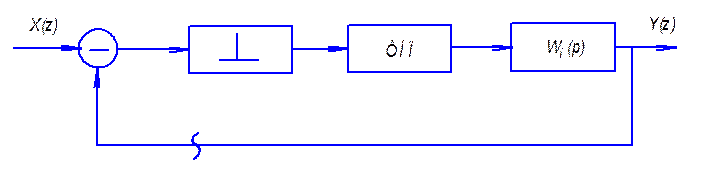
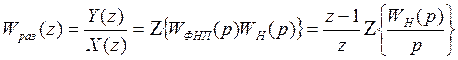
Для непрерывных систем: 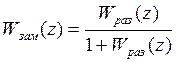
Вводится характеристическое уравнение замкнутой
системы: ![]()
Характерные собственные динамические свойства ![]() -система будет устойчива.
-система будет устойчива.
Корни характеристического уравнения:
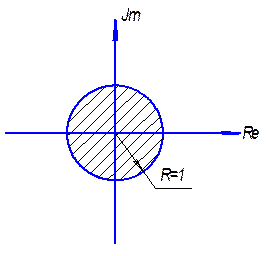
Если вне окружности - система не устойчива,
Если на окружности - система на границе устойчивости,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.