Основы теории линейных импульсных (цифровых) систем управления, страница 6

Гармоническая лианеризация нелинейной характеристики заключается в том, что записывается ряд Фурье для выходной переменной нелинейного элемента при гармоническом входном сигнале, далее используется только первая гармоника, в результате чего получается аналитическая линейная зависимость между выходным и входным сигналами нелинейного элемента.

Задача:

В системе нет входного сигнала, имеют ли место установившиеся автоколебания?

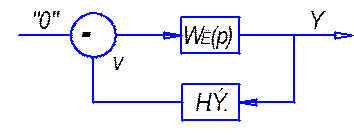
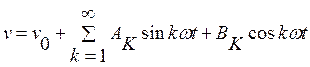- сигнал поступает на линейную часть системызаменяем рj Прямоугольный сигнал становится более гибким из-за наличия W_НЭ:

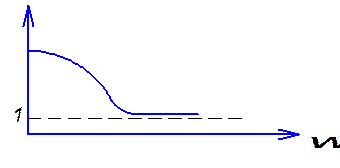
Методы гармонического баланса должны определять есть ли в системе, состоящей из W_Л и нелинейного элемента, автоколебания. Если есть, то они описываются уравнением. Проходя через нелинейный элемент, гармонические колебания искажаются, форма их зависит от нелинейного элемента, но период остается прежним, меняется амплитуда и форма. Форму представляем в виде ряда Фурье. Синусоидальные гармоники возбуждают нелинейность однозначную, если неоднозначную, то идет сдвиг. Этот сигнал идет к W_Л и преобразуется, то есть меняется коэффициентна выходе сигнал может быть такой же частоты и амплитуды,но другой формы(гармонический баланс = циркуляционное кольцо = автоколебания ).

1.  На первом этапе при работе с методом гармонического баланса необходимо свести систему к виду:

2.  Гипотеза фильтра:

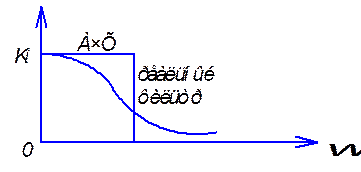Вводится предположение, что линейная часть САУ представляет собой фильтр низких частот с прямоугольной АЧХ, причем этот фильтр пропускает только первую гармонику сложного периодического сигнала, поступающего с нелинейного элемента. Все остальные гармоники полностью подавляются. Гипотеза фильтра обязательно проверяется после определения частоты возможных автоколебаний.

    

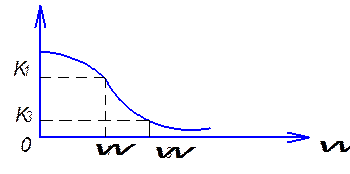
K₁K₃- гипотеза выполняется с погрешностями, если неравенство не соблюдается необходимо уточнение.

3.  Для определения возможных автоколебаний вводится понятие уравнения гармонического баланса, оно аналогично характеристическому уравнению, рассмотренному в пункте 1.

1+, где -коэффициент гармонической лианеризация нелине йного элемента.

4.  Коэффициенты гармонической лианеризации:

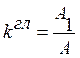 остальные коэффициенты отбрасываются,так как они слабо влияют на          гармонический баланс.

5.  Уравнение гармонического баланса и его решение.

6.  Проверка гипотезы фильтра(строится АФХ и сравниваются коэффициенты k₁ с k₃).

Лекция13

Гармоническая линеаризация.

Метод гармонической линеаризации применяется для приближенного определения периодических решений (автоколебаний) и устойчивости нелинейных систем любого порядка.

Метод гармонической линеаризации является мощным средством исследования нелинейных автоматических систем в смысле простоты и довольно большой универсальности его аппарата в применении к самым различным нелинейностям. Но нужно иметь ввиду, что метод решает задачу приближенно и имеются определенные ограничения его применения.

Вычисление коэффициентов гармонической линеаризации.

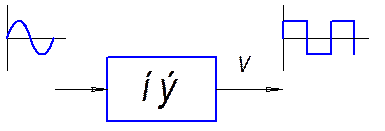
Рис1.

Если характеристики одинаковые, то отсутствует .

Коэффициент гармонической линеаризации ()- отношение первой гармоники выходного сигнала к входному сигналу.

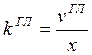
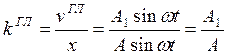
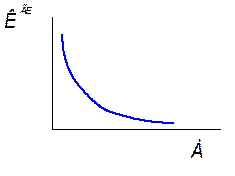
Рис2.

Рис3.

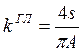
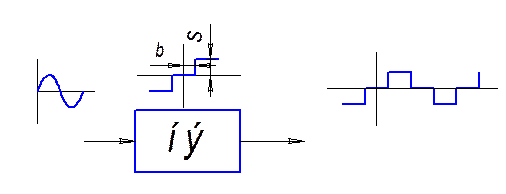
Рис4.

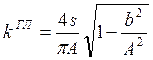
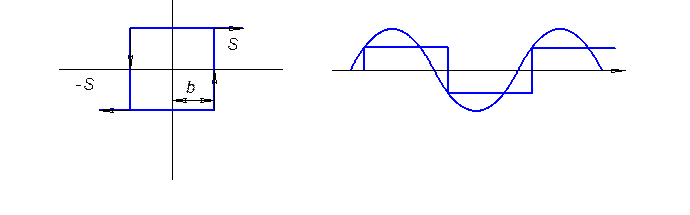
Рис5.

                   

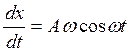
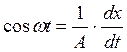
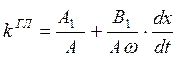
Метод  Гольдфарба.

Л.С. Гольдфарб предложил графо-аналитический способ решения уравнения гармонически линеаризованной системы: 

, где  зависит от

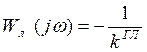
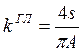
Рис6.

В случае двух решений уравнения Гольдфарба возникает вопрос какое из них устойчивое.

Устойчивым решением является решение, когда при увеличении амплитуды линия 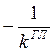  выходит из годографа АФХ линейной части системы.

Лекция14

Метод Попова.

Метод Попова основан на аналитическом решении характеристического уравнения замкнутой гармонически линеаризованной системы. При этом находятся формулы, определяющие непосредственно зависимость амплитуды и частоты автоколебаний от параметров системы. Метод Попова позволяет исследовать нелинейные системы с несколькими нелинейностями, разделенные линейными инерционными звеньями.

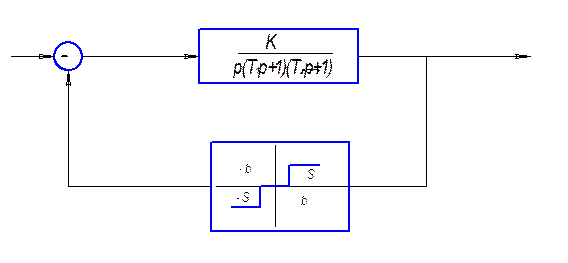
Рис1.

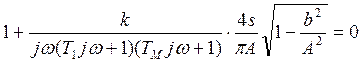
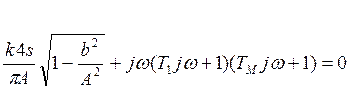
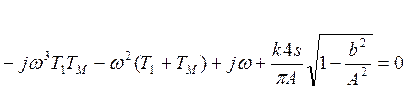
Выделяем вещественную и мнимую части:

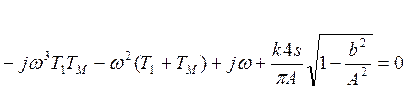
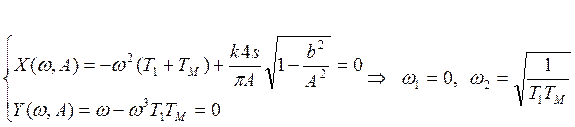
Если уравнения не решаемы, то колебаний нет.