Фазовые траектории, определяемые уравнением (9.2) имеют следующие свойства:
При ![]() переменная
переменная ![]() всегда
возрастает;
всегда
возрастает;
При ![]() переменная
переменная ![]() всегда
убывает;
всегда
убывает;
При возрастании ![]() движение изображающей
точки происходит слева направо в верхней полуплоскости и справа налево в
нижней полуплоскости;
движение изображающей
точки происходит слева направо в верхней полуплоскости и справа налево в
нижней полуплоскости;
При ![]() значение
значение ![]() ,
поэтому в точках пересечения фазовых траекторий с осью абсцисс
,
поэтому в точках пересечения фазовых траекторий с осью абсцисс ![]() касательные к ним перпендикулярны к оси
касательные к ним перпендикулярны к оси ![]()
Если уравнение (9.2) трудно проинтегрировать, то фазовые траектории
можно построить по методу изоклин. Изоклины представляют собой
геометрическое место всех точек фазовой плоскости, для которых наклон фазовой
траектории равен постоянному значению ![]() . Пусть,
например,
. Пусть,
например, ![]() , тогда вместо (9.2) можно записать
уравнение:
, тогда вместо (9.2) можно записать
уравнение:
![]() ,
,
Из которого получается уравнение изоклины
![]()
Где ![]() - угловой коэффициент изоклины.
- угловой коэффициент изоклины.
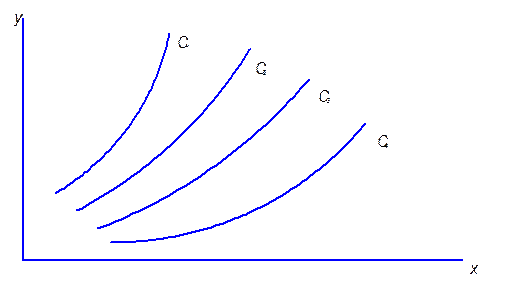 Задаваясь различными постоянными значениями наклона
Задаваясь различными постоянными значениями наклона ![]() , можно построить семейство изоклин, каждая
из которых имеет угловой коэффициент
, можно построить семейство изоклин, каждая
из которых имеет угловой коэффициент ![]() для данной системы.
Семейство изоклин используется для построения фазовых траекторий с различными
начальными условиями при помощи отрезков прямых, направленных в соответствии с
наклоном, определяемым изоклинами.
для данной системы.
Семейство изоклин используется для построения фазовых траекторий с различными
начальными условиями при помощи отрезков прямых, направленных в соответствии с
наклоном, определяемым изоклинами.
Рис. 9.2
Лекция 10
Задача.
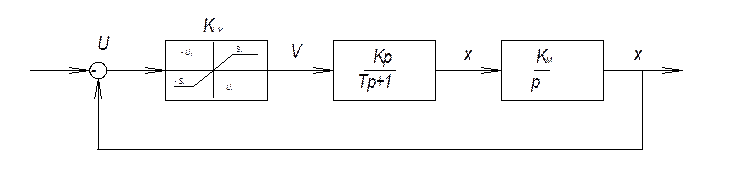
Величины ограничений ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
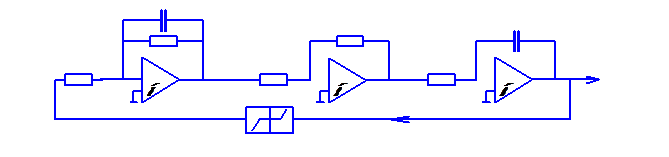
Характеристическое уравнение позволяет следить за свободным перемещением системы.
![]()
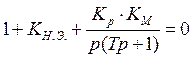
Приводим к общему знаменателю:
![]() т.к. на вход подается x
т.к. на вход подается x
Преобразуем операт. Уравнение в дифференциальное:
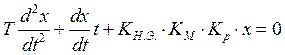
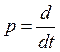
Фазовая плоскость описывается: 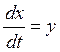
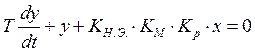
![]()
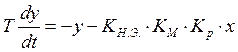
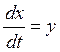
Разделим первое уравнение на втрое:
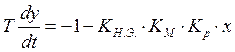
Рис.10.1
![]()
1.
![]() ;
; ![]()
2.
![]() ;
; ![]()
![]()
3.
![]() ;
; ![]()
![]()

Рис. 10.2 Фазовая плоскость
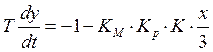
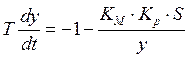
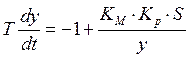
Они описывают три уравнения листа.
Если проинтегрировать эти уравнения, то получиться движение у от х
Способы:
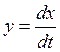
Изоклина
– линия фазовой плоскости через которую проходит все фазовые траектории
проходящие с одним наклоном к оси ![]()
Чтобы получить
изоклину: нужно 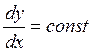
|
угол |
|
|
|
0 |
0 |
|
|
30 |
|
|
|
60 |
|
|
|
90 |
|
|
|
120 |
|
|
Уравнение
изоклины: 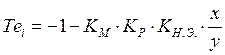
Для второй
изоклины (2-го уравнения): 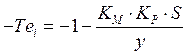
Угол наклона от стартовой точки выбирается самостоятельно.
При переходе с листа на лиcт происходит переход переменных (постоянных)
Лекция11
Рассмотрим нелинейный элемент в виде петли гистерезиса:
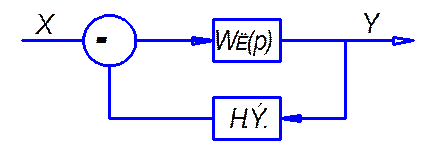
Петля гистерезиса Картина фазовых траекторий
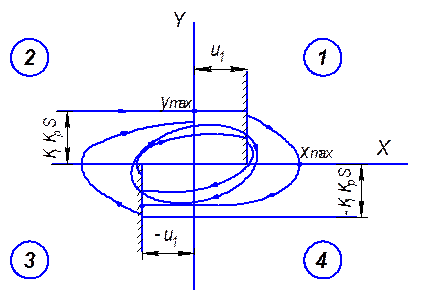
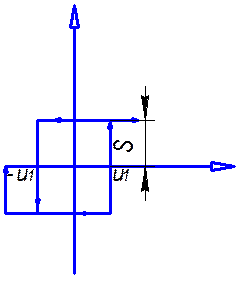
S- предельные значения
функции; Увеличение сигнала соответствует y>0![]() на
на
u- зона линейности; уровне +U1. Данная картина показывает, что в данной системе протекает процесс установившихся колебаний и при малых начальных отклонениях процесс является расходящимся, а при больших-сходящимся.
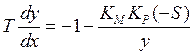

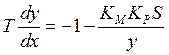
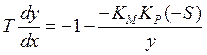

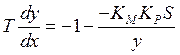

Предположим:
![]()
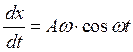 можем сделать оценку A и
можем сделать оценку A и ![]()
![]() A=
A=![]()
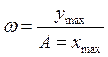
С нелинейными элементами вида гистерезиса чаще всего возникают установившиеся колебания.
Рассмотрим трехпозиционное реле, если реле имеет зону нечувствительности, то его нелинейную характеристику можно разделить на три участка:
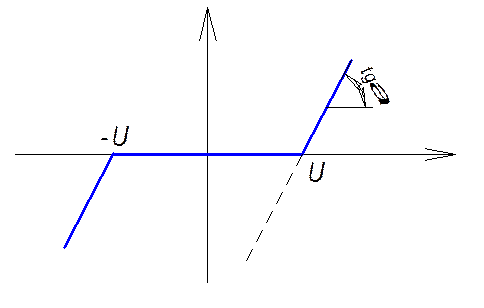
Дифференциальные уравнения фазовых траекторий будут иметь вид:
1.
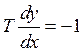
2. 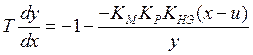 ;
; ![]()
3. 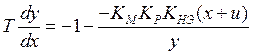 ;
; ![]() Фазовый портрет:
Фазовый портрет:
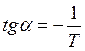
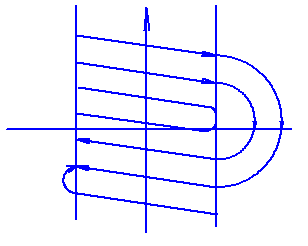
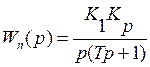
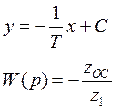
Построение переходного процесса по фазовой траектории.
Состояние автоматической системы в любой момент времени может быть охарактеризовано значениями рассматриваемой переменной и (n-1) ее производных. Каждому определенному переходному процессу автоматической системы в фазовом пространстве соответствует определенная траектория движения изображающей точки(точка, соответствующая состоянию системы в фазовом пространстве).Начальное положение изображающей точки определяется начальными условиями свободного движения системы. При равновесии системы все производные рассматриваемой переменной равны нулю; соответствующие этому точки фазового пространства называются особыми. Наиболее наглядно фазовые траектории могут быть представлены на фазовой плоскости.
Задача:
Оценить качество и время переходного процесса, соответствующего свободному движению системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.