Основы теории линейных импульсных (цифровых) систем управления, страница 5

Решение:

Предполагаем, что координата y заменяется наконечное приращениек .

Для удобства разбиваем отрезок фазовой траектории на участки x() и их размечаем:

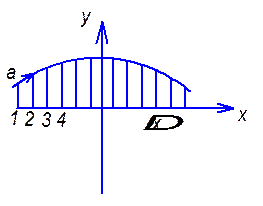
При изображении  процессов на фазовой плоскости  уравнения второго порядка заменяют эквивалентными первого порядка.

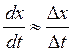Далее для каждого участка оцениваем среднее значение yy=, где

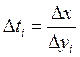
Фазовые траектории обладают следующими свойствами:

При y>0 переменная x всегда возрастает

При y<0 переменная x всегда убывает.

При возрастании t движение изображающей точки происходит слева направо в верхней полуплоскости и справа налево в нижней полуплоскости. Если трудно проинтегрировать уравнения, то фазовые траектории можно построить по методу изоклин. Изоклины- геометрическое место всех точек фазовой плоскости, для которых наклон фазовой траектории равен постоянному значению С_i. Пусть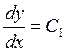, уравнение изоклин:, где  -угловой коэффициент изоклины.

Просчитываем для каждого значения и строим график:

Метод фазовой плоскости переводит аналитическую задачу решения дифференциальных уравнений второго порядка с любыми нелинейностями статического типа в графическую задачу. Задача решается следующим образом на фазовой плоскости задаем координаты x , а выходная координата линейной части системы y=.

Эта фазовая плоскость обладает особыми свойствами, которые позволяют судить о виде решения дифференциальных уравнений. Анализируя вид фазовой траектории можно определить какого типа особая точка характеризует поведение исследуемой САУ. Зная тип особой точки можно судить о виде движения САУ в свободном состоянии, т.е. судить о том будет ли сходиться или расходиться переходной процесс, будет ли он колебательный или апериодический, будут ли иметь место автоколебания в системе и какого рода они будут, устойчивыми или условно-устойчивыми.

Можно по виду фазовой траектории сделать оценку переходного процесса и даже его построить.

Достоинства метода фазовой плоскости:

Ø  наглядность

Ø  точность метода

Ø  малый объем вычислительной работы

Недостатки:

Ø  ограничен уравнениями второго порядка

Ø  фазовые траектории не отражают темпов изменения координаты по времени

Ø  относительно трудоемкий.

Лекция 12

Методы гармонического баланса

Лианеризация производится в частотной области. Этот метод является приближенным, порядок уравнений не ограничен(чем выше, тем лучше).

Гармоническая лианеризация.

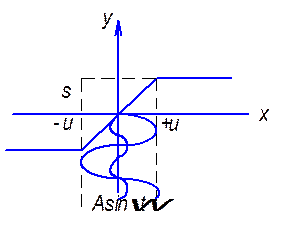y=kAsin, если сигнал меньше уровня насыщения

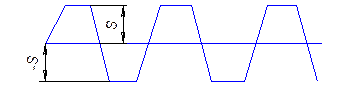Сигнал на выходе больше уровня насыщения , но меньше выходного сигнала. А=А_ВХОДk

Сигнал получается периодический, искаженный сложной формы.

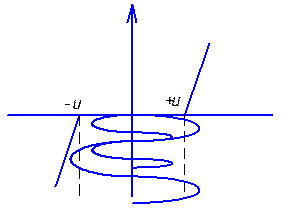                Меньше(-U;+U)на выходе 0.

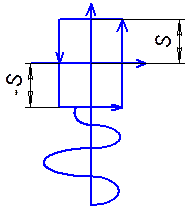
Для идеальной релейной характеристике построены графики sin и , которые определяют величину комплексного коэффициента усиления. Нелинейная характеристика в данном случае однозначна и симметрична и коэффициент усиления равен нулю.

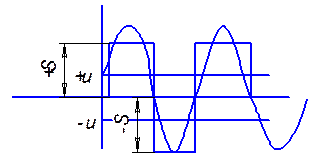
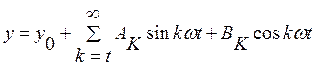- ряд Фурье.

Если нелинейные функции имеют симметрию относительно оси, то отсутствует в выходном сигнале. Если нелинейный элемент имеет однозначную величину, то cos отсутствует(cos отвечает за смещение по фазе относительно входного сигнала).Следовательно на линейную часть системы действует сигнал, содержащий весь спектр частот. Таким образом, на выходе системы установятся негармонические колебания, их спектр будет содержать все те же частоты, что и спектр колебаний на выходе нелинейного элемента, но амплитуда каждой гармоники будет зависеть от свойств линейной части и изменяться в раз. Амплитудная характеристика линейной части системы позволяет установить, во сколько раз изменяются амплитуды всех гармоник, порожденных нелинейностью, при прохождении их через линейную часть системы. Для этого надо при заданном значении  основной гармоники рассмотреть ординаты амплитудной характеристики k(j)  при ,….. Если ордината А₁ при  несоизмеримо больше амплитуд более высоких гармоник ,то система является фильтром и не пропускает высшие гармоники, порождаемые нелинейностью. Если в замкнутой системе имеются автоколебания , то при выходном сигнале х=0 в контуре системы есть сигнал, обеспечивающий автоколебания. Определение автоколебаний связано с предположением, что на выход нелинейного элемента поступает гармонический сигнал, а линейнаячастьгасит все высшие гармоники.