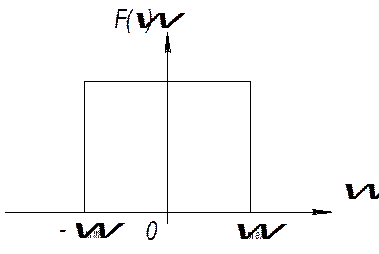Основы теории линейных импульсных (цифровых) систем управления, страница 3

Если импульсный сигнал восстанавливается с помощью полосового фильтра       имеющую частотную характеристику, то такая операция может быть осуществлена без потерь информации при условии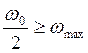     

Лекция 8

Нелинейные САУ.

Нелинейной системой автоматического регулирования называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением. Перечислим виды нелинейных звеньев:

1.  звено релейного типа (рис. 8.1);

2.  звено с кусочно – линейной характеристикой (рис. 8.2);

3.  звено с криволинейной характеристикой любого очертания;

4.  звено, уравнение которого содержит произведение переменных или их производных и других их комбинаций;

5.  нелинейное импульсное звено;

6.  логическое звено.

Часто при исследовании нелинейных систем автоматического регулирования удается выделить нелинейность так, чтобы она описывалась непосредственно зависимостью между выходной и входной величинами

которая может иметь любую форму (релейного типа, кусочно – линейного или криволинейного).

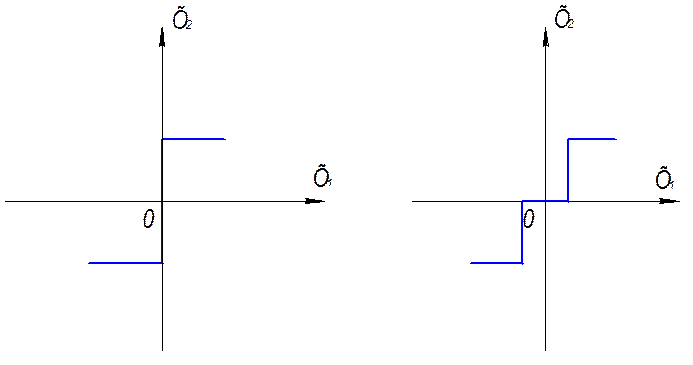
Рис. 8.1

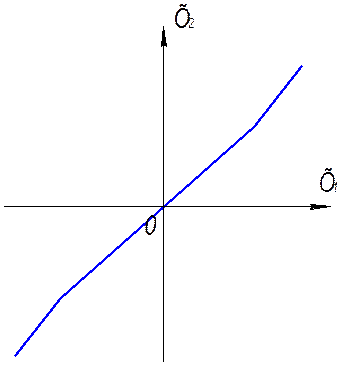Рис. 8.2

Нелинейные звенья это звенья уравнения которых не могут быть линеаризованы стандартными методами в связи с тем, что в некоторых точках первая производная стремится к бесконечности.

Существует классификация нелинейных элементов.

Нелинейные элементы делятся на:

1.  симметричные (рис. 8.3а);

2.  несимметричные (рис. 8.3б);

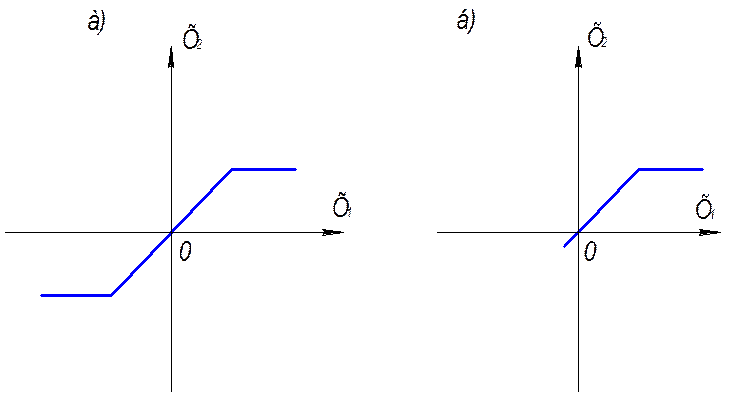
Рис. 8.3

3.  Однозначные;

4.  Неоднозначные, т.е. одному значению функции соответствует два значения аргумента (рис. 8.4);

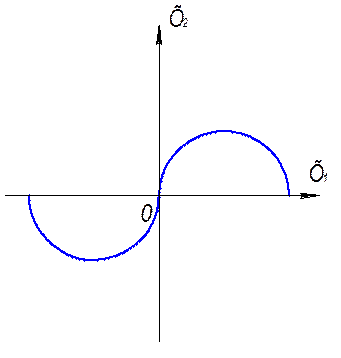Рис. 8.4

5.  Динамические нелинейные элементы (усилитель с ограничением рис. 8.5а);

6.  Статические нелинейные элементы (усилитель с зоной нечувствительности рис. 8.5б).

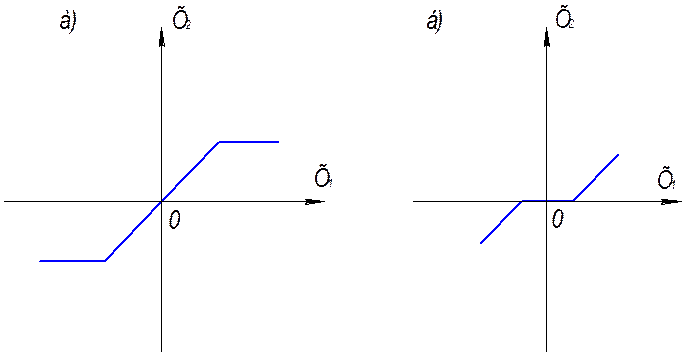   Рис. 8.5

При анализе нелинейных систем структурную схему приводят к расчетному виду (рис. 8.6).

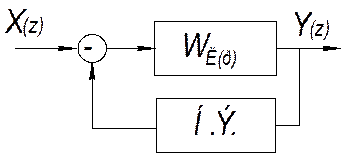Рис. 8.6

·  Н.Э. – нелинейный элемент.

Задачей анализа непрерывных систем является установление факта установившихся автоколебаний в контуре системы. Если автоколебания имеют место, то определяется их частота и амплитуда.

Существует два вида задач связанных с нелинейными системами:

1.  Задача исключения автоколебаний в САУ;

2.  Расчет системы чтобы были установившиеся устойчивые автоколебания.

Лекция 9

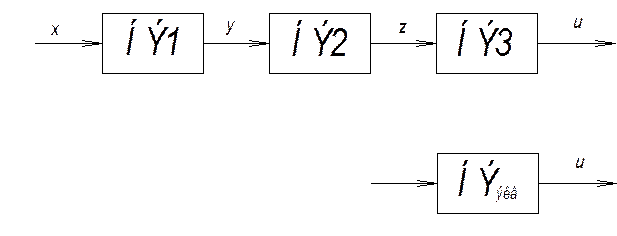
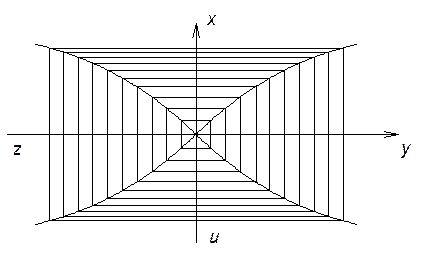
Рис.9.1 Усилитель с насыщением

Метод фазовой плоскости

Состояние автоматической системы в любой момент времени может быть охарактеризовано значениями рассматриваемой переменной и  ее производных. Для рассмотрения системы -го порядка необходимо использовать -мерное пространство, содержащее осей координат.

Если в данный момент времени по указанным осям отложить значения переменной  ее производных, то будет получена точка, изображающая состояние системы. Указанное пространство называется фазовым, а точка, соответствующая состоянию системы в фазовом пространстве, -  изображающей.

При равновесии системы все производные рассматриваемой переменной равны нулю; соответствующие этому точки фазового пространства называются  особыми. Совокупность фазовых траекторий для всевозможный начальных отклонений вместе с особыми траекториями и точками называется фазовым портретом системы.

Наиболее наглядно фазовые траектории могут быть представлены для систем второго порядка в системе координат (переменная величина) и ( скорость изменения переменной величины), т.е. на фазовой плоскости. Метод является частным случаем метода фазового пространства.       Недостатком метода является его ограничение с системами второго порядка.

В некоторых случая можно аппроксимировать системы высокого порядка системой второго порядка с эквивалентным запаздыванием, что расширяет область применения метода фазовой плоскости. При изображении процессов на фазовой плоскости уравнение второго порядка заменяют эквивалентными уравнениями первого порядка:

;

.

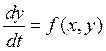
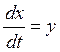Чтобы изобразить процесс на фазовой плоскости, из уравнений (9.1 ) исключают время, для  чего делят первое уравнение на второе:

     

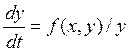
После решения нелинейного дифференциального уравнения (9.2) получается уравнение фазовой траектории:

         

Которое определяет кривую на фазовой плоскости. Каждой совокупности начальных условий ,   будет соответствовать свой решение  и своя фазовая траектория.

Интегрирование уравнения (9.2) может быть осуществлено аналитически (в простейших случаях), графически, численно и при помощи вычислительных машин.