Основы теории линейных импульсных (цифровых) систем управления, страница 2

Если в окружности - система устойчива.

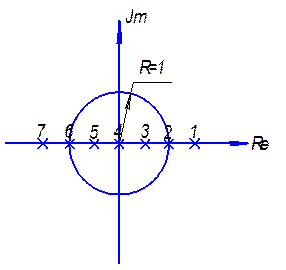
Один корень.

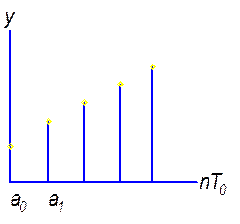
1.  Процесс вне окружности – расходящийся 

  

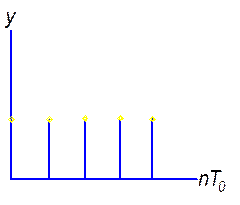
2.

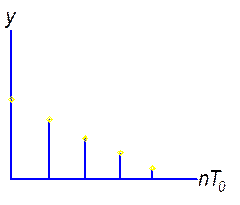
3.  Сходящийся процесс

4.  Корень находится по центру

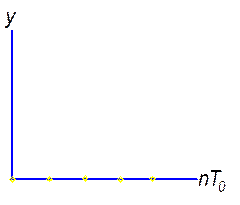
5.  Устойчивая, но колебания чередуются по знаку ординаты

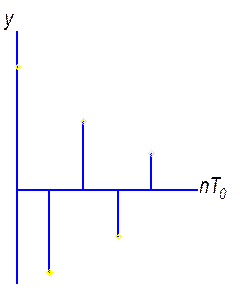
6.  Единичное значение, чередуется по знаку

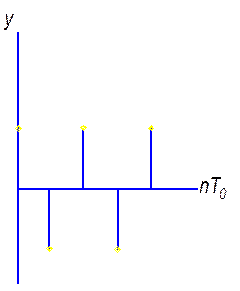
7.

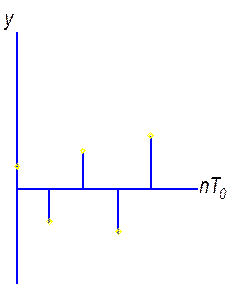
Если два корня.

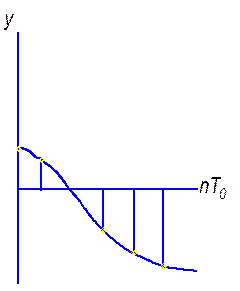
1.  Неустойчивая система

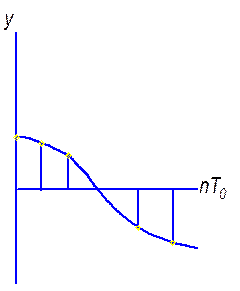
2.  Граница устойчивости

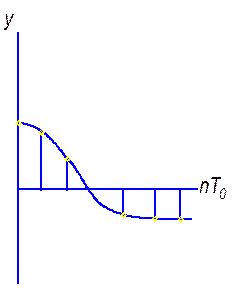
3.  Устойчивая система

4.

5.

W-комплексная функция зона чувствительности  

Билинейное преобразование

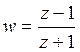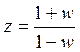;  -используем для  решения задач с импульсными системами.

получим псевдопреобразование системы

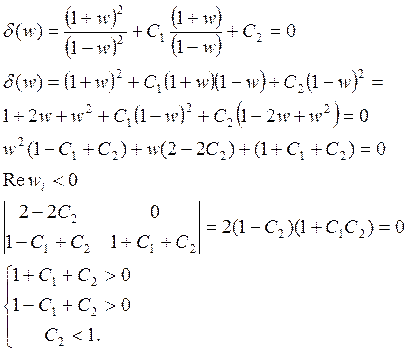
Лекция5

Использование критерия Гурвица на устойчивость системы

Пример:

При К=10        Найти Т₀=?

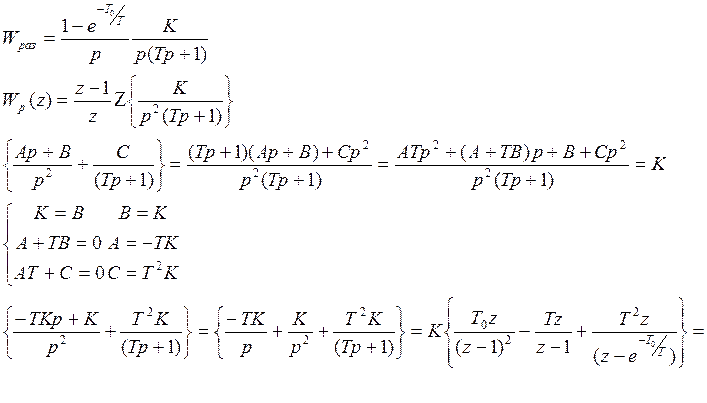
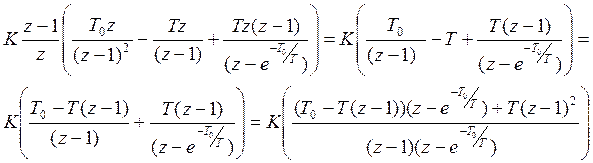
В результате преобразований приводим к такому виду уравнение:

Решая это уравнение находим T₀.

Лекция 5

Устойчивость и качество импульсных систем регулирования (продолжение).

Рассмотрим систему:

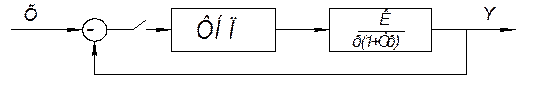
При К=10, найти -?. При котором система будет находится на границе устойчивости.

Запишем передаточную функцию:

 

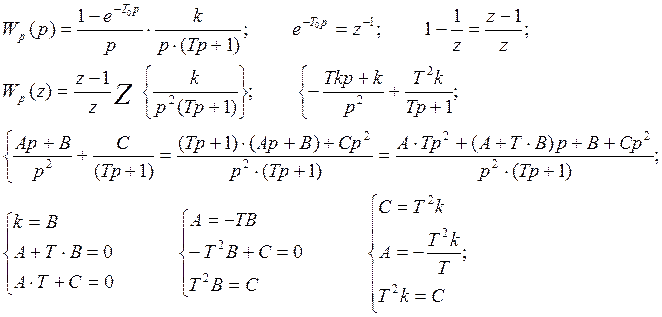
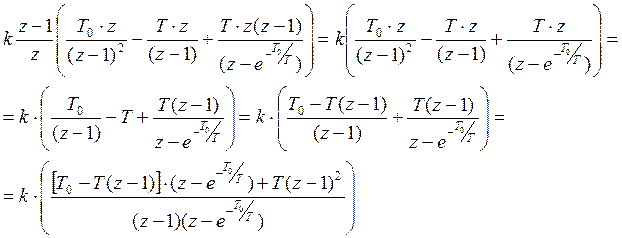
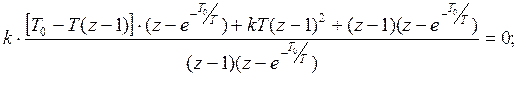
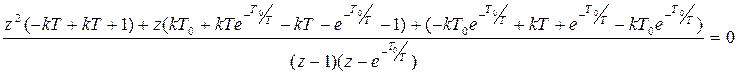
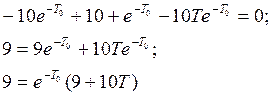
Лекция 6

Цифровое моделирование непрерывных объектов управления.

Рассмотрим систему:

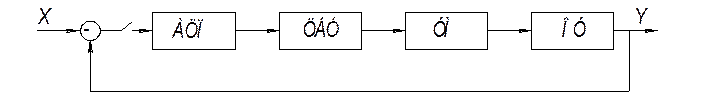
АЦП – аналого-цифровой преобразовать;

ЦБУ – цифровой блок управления;

УМ – усилитель мощности;

ОУ – операционный усилитель;

 - оператор сдвига.

Используя, оператор сдвига реализовать цифровой интегратор:

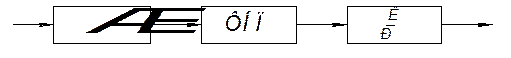
Запишем передаточную функцию:

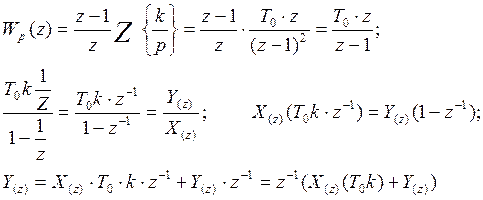
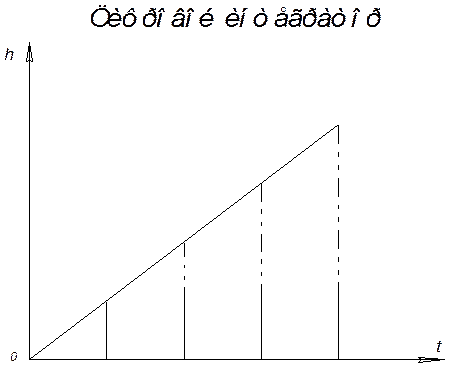
Реализуем более сложную функцию:

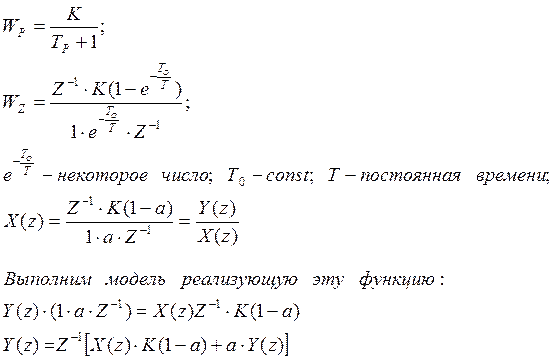
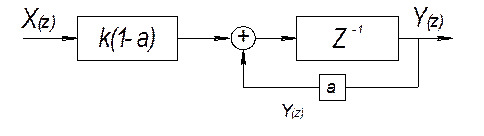
При

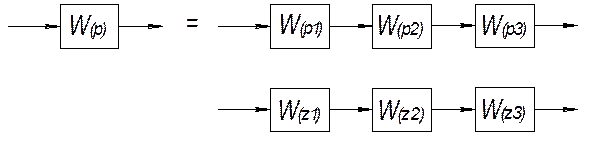
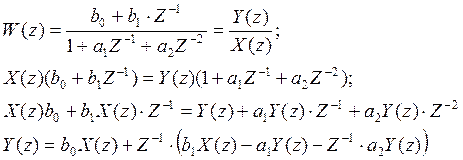
Реализованная модель функции:

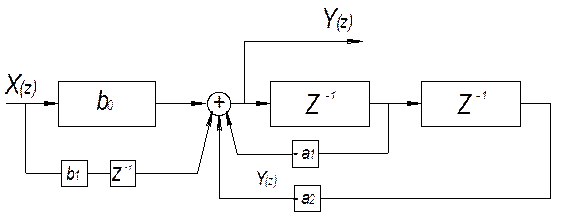
Если порядок знаменателя больше чем порядок числителя, то можно представить любое сложное звено:

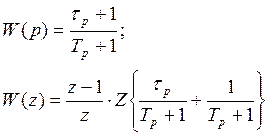
Лекция 7

Частотные методы анализа и синтез импульсных САУ.

В импульсных системах автоматического регулирования устойчивость будет иметь место, если все полюсы передаточной функции замкнутой системы, т.е. корни характеристического уравнения, лежат в левой полуплоскости корней. Граница устойчивости является мнимая ось. Для построения области устойчивости в плоскости комплексной величины z  сделаем подстановку p=jw и менять затем частоту w в пределах -¥ до +¥. Таким образом получаем, получаем  .

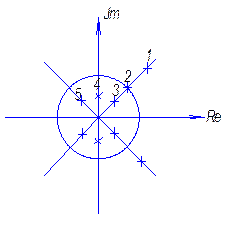
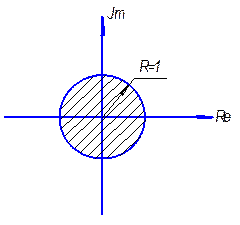
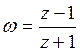Для уравнения более высокого порядка исследование устойчивости усложняется. Для облегчения задачи иногда используются так называемое w - преобразование, посредством которого окружность единичного радиуса отображается на мнимую ось плоскости комплексной величины w. Для преобразования используется подстановка   или соответственно   (рис 7.1).

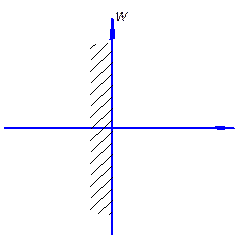
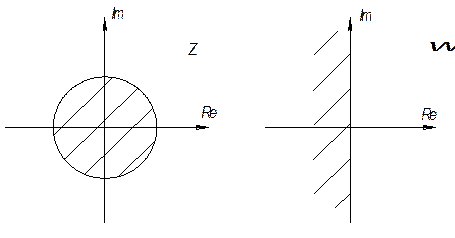     Рис. 7.1

Можно рассматривать как псевдочастоту:

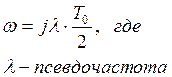
Введенная псевдочастота позволяет рассматривать импульсные системы разработанными методами для неприрывных систем.

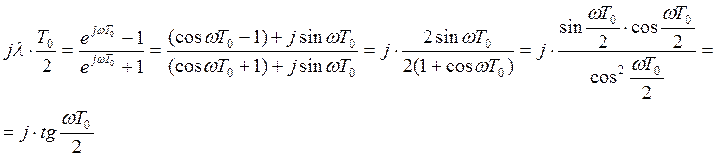
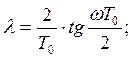
Следуют выводы:

При частоте w близкое к 0, то и l@0,

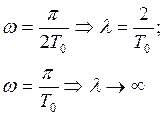
Задание:

Требуется построить логарифмическую частотную характеристику в области псевдочастоты l  импульсной системы с непрерывной частью:

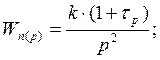
Получаем дискретную передаточную функцию разомкнутой САУ:

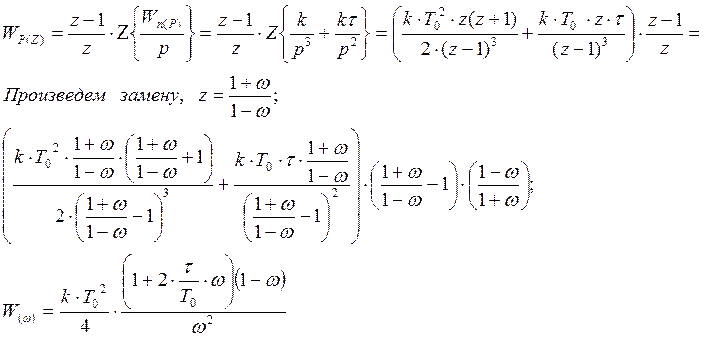
Переходим к псевдочастоте заменяем:

;

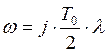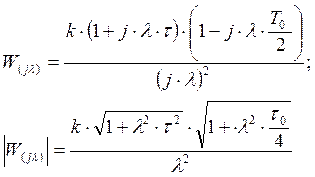
Строим ЛЧХ:

1 вид: Цифровое корректирующее устройство,

2 вид: Дискретное корректирующее устройство,

3 вид: Устройство с амплетудно - корректирующей модуляцией.

Методика расчета корректирующего устройства для

импульсных систем

1.  Привести импульсную САУ к расчетному виду.

2.  Определить дискретную передаточную функцию разомкнутой САУ.

3.  Определить комплексный коэффициент передачи импульсной САУ в области псевдочастоты.

Последовательно переходя от переменной z к переменной w  .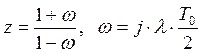

4.  Построить модуль логарифмической частотной характеристики разомкнутой САУ функции псевдочастоты l.

5.  На основании требований к качеству САУ построить желаемую ЛАЧХ.

6.  Определить ЛАЧХ корректирующего устройства путем вычитания  

7.  Если корректирующее устройство реализуется на устройстве сдвига или временной задержки определить дискретную передаточную функцию этого корректирующего устройства.

8.  В случае если КУ реализуется на непрерывных частотных элементах перейти к непрерывной передаточной функции .

Теорема о прерывании

Теорема Котельникова – Шеннона

Позволяет связать импульсные и непрерывные сигналы при которых квантование не искажает ??????????????

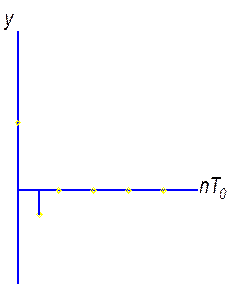
Если непрерывный сигнал имеет непрерывную плоскость  частот,

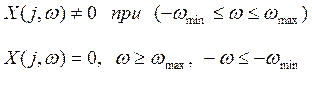  этот сигнал подвергается квантованию с периодом  (рис. 7.2).

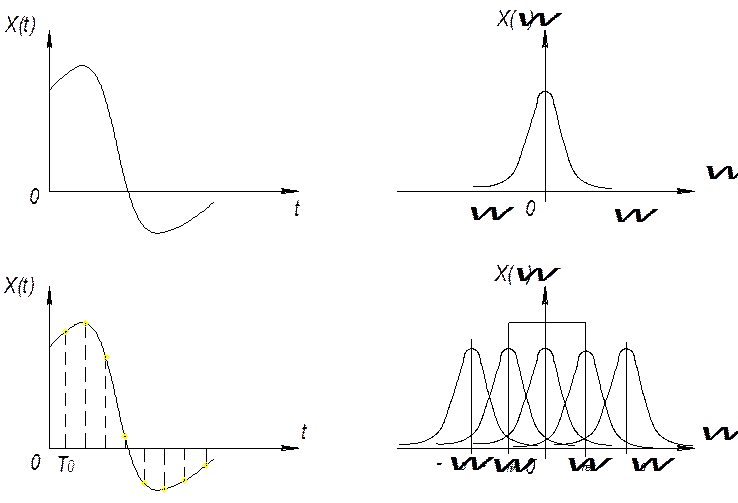Рис. 7.2

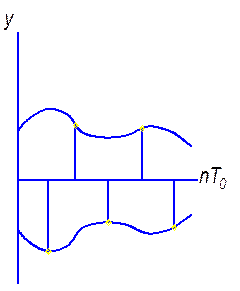
При квантовании сигнала в спектре появляется высокочастотное квантование и это все многократно повторяется.