МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Сибирский государственный индустриальный университет
Кафедра высшей математики
РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ
РАБОТ ПО КУРСУ «ВЫСШАЯ МАТЕМАТИКА»
2 семестр для студентов-заочников
Издание СибГИУ Новокузнецк 1999
УДК 519.075
Даны примеры и рекомендации по выполнению контрольных работ 4-6 по высшей математике для студентов-заочников 1 курса по программе второго семестра.
Рецензент – кафедра физики Сибирского государственного инду-стриального университета ( зав. кафедрой профессор Громов В.Е.)
Печатается по решению редакционно-издательского совета университета
ВВЕДЕНИЕ
Данные методические указания предназначены в помощь студентам-заочникам 1-го курса при выполнении ими контрольных работ по математике за второй семестр (контрольные работы №4, №5, №6). Номера задач по вариантам в сборнике заданий, распределены следующим образом
|
Ва-ри-ант |
Номера заданий для контрольных работ |
||
|
№4 |
№5 |
№6 |
|
|
1 2 3 4 5 6 7 8 9 10 |
171 181 191 201 172 182 192 202 173 183 193 203 174 184 194 204 175 185 195 205 176 186 196 206 177 187 197 207 178 188 198 208 179 189 199 209 180 190 200 210 |
281301 311 282 302 312 283 303 313 284 304 314 285 305 315 286 306 316 287 307 317 288 308 318 289 309 319 290 310 320 |
321 331 341 351 361 322 332 342 352 362 323 333 343 3 53 363 324 334 344 354 364 325 335 345 355 365 326 336 346 356 366 327 337 347 357 367 328 338 348 358 368 329 339 349 359 369 330 340 350 360 370 |
В конце данных указаний даны теоретические вопросы экзамена-ционных билетов за 2 семестр.
Тема: Приложение производной
Задание 1 (171-180). Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [ a; b].
Указания к решению. Наибольшее и наименьшее значения на отрезке непрерывная функция принимает либо на границах отрезка, либо в тех точках отрезка, где производная этой функции равна нулю или не существует. Поэтому для нахождения этих значений надо найти значения функции во всех перечисленных выше точках и затем определить среди них наибольшее и наименьшее.
Пример. y=x4 – 2x2 +5 ; [ -2; 2].
Решение. y¢=4x3 – 4x, y¢=0, то 4x3 – 4x=0 Þ 4x(x+1)(x-1)=0 Þ x1=0, x2=-1, x3=1. Все корни уравнения y¢ =0 попадают в отрезок [-2; 2], поэтому определим значения функции во всех этих точках, а также на концах отрезка: у(-2)=(-2)4 –2(-2)2 +5=13, у(-1)=4, у(0)=5, у(1)=4, у(2)=13.
Ответ: ymax=y(-2)=y(-2)=13; ymin=y(-1)=y(1)=4.
Задание 2. (181-190). Решить задачу оптимизации относительно размеров геометрической фигуры, количества расходуемого материала и т.д.
Указания к решению. ![]() Для решения такой задачи
необходимо составить целевую функцию и затем исследовать ее на экстремум с
помощью производной.
Для решения такой задачи
необходимо составить целевую функцию и затем исследовать ее на экстремум с
помощью производной.
Пример. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим.
Решение. Пусть h-высота воронки, r- радиус верхней окружности,
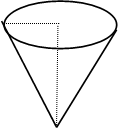 r
r
l h
l-образующая. Тогда ![]() , а
объем
, а
объем 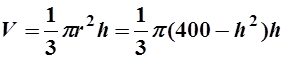
Функция
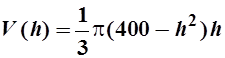
и является целевой. Отсюда
находим
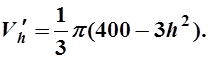 Тогда
Тогда 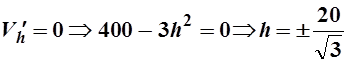 . Так
как h может принимать только положительные значения, то остается единственное
значение
. Так
как h может принимать только положительные значения, то остается единственное
значение 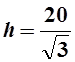 . Исследуем знак производной
. Исследуем знак производной 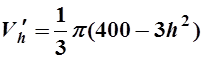 при переходе через точку
при переходе через точку 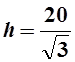 . Имеем
. Имеем ![]() , если
, если 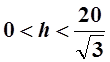 и
и ![]() , если
, если 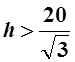 . Это означает, что в точке
. Это означает, что в точке 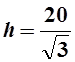 функция V(h) принимает наибольшее значение
функция V(h) принимает наибольшее значение
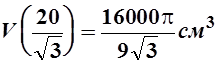 .
.
Ответ: 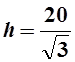 см.
см.
Задания 3, 4 (191-210). Исследовать методами дифференциального исчисления функцию y=f(x) и, используя результаты исследования, построить ее график.
Указания к решению. При построения графика функции y=f(x) необходимо выяснить его характерные особенности. Для этого надо:
1. Найти область определения функции и определить ее поведение на границах области определения; найти вертикальные асимптоты.
2. Исследовать функцию на четность и нечетность, периодичность.
3. Найти наклонные асимптоты.
4. Найти точки пересечения графика с осями координат.
5. Найти интервалы возрастания и убывания функции, ее экстремумы и вычислить значения функции в этих точках.
6. Найти интервалы выпуклости и вогнутости графика, точки перегиба и вычислить значения функции в этих точках.
7. Определить дополнительные значения функции в произвольно выбранных точках из области определения.
Пример. Построить график функции 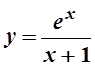 .
.
Решение. 1. Область определения![]() . На
границах области определения
. На
границах области определения
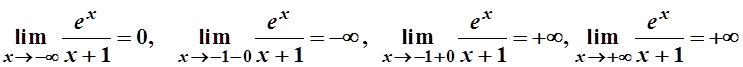 Отсюда видно, что х=-1 – вертикальная
асимптота.
Отсюда видно, что х=-1 – вертикальная
асимптота.
2.
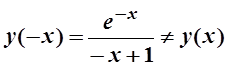 - функция не является четной,
- функция не является четной,
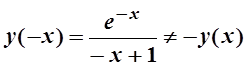 -функция не является нечетной.
-функция не является нечетной.
Функция непериодична, так как у(х+Т) ¹ у(х) при любом Т ¹0.
3. Ищем наклонные асимптоты в виде y=kx+b.
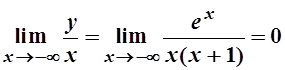 , поэтому k=o,
, поэтому k=o,
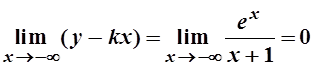 , поэтому b=0.
, поэтому b=0.
Таким
образом при ![]() - является асимптотой.
- является асимптотой.
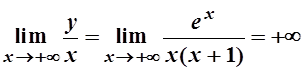 , поэтому при
, поэтому при ![]() асимптоты
нет.
асимптоты
нет.
4. Если х=0, то у=1; у¹0 при любых х.
5.
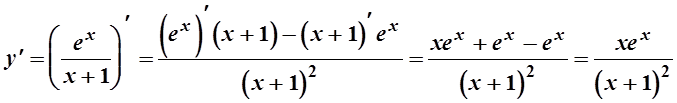 .
.
у¢=0 при хе х =0, то есть при х=0. у¢ - не определена при х =-1. Исследуем знак у¢:
![]()
![]()
![]() y < 0 y <0 у¢>0
y < 0 y <0 у¢>0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.