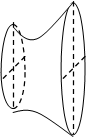
Объем тела, образованного вращением вокруг оси Ох плоской области, ограниченной прямыми х=а, х=b, y=0 и графиком функции y=f(x) ³ 0 при a £ x £ b, находится по формуле:
![]() у
у
 |
![]()
![]()

![]() а b
х
а b
х
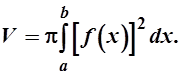
Если плоская область, ограниченная линиями у=с, y=d, x=0, x=j(y) вращается вокруг оси Оу, то объем полученного тела находится по формуле
![]() у
у
![]()
![]()
![]()
![]()
![]()
![]() d
d
 |
![]()
![]()
![]()
![]()
![]() с
с

![]() х
х
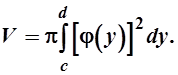
Длина кривой L в зависимости от способа ее задания определяется следующими формулами
![]() а) y
а) y
 |
y=f(x)
![]() a b
x
a b
x
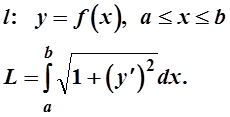
![]() б) y
б) y
![]()

![]() y(b)
y(b)
![]()
![]() y(a)
y(a)
![]() x(a) x(b) x
x(a) x(b) x
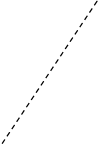
 r=r(j)
r=r(j)
 b
b
![]()
![]()
![]() a
a
Примеры.
 |
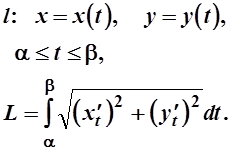
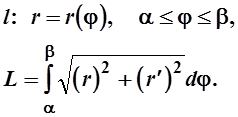
1. Вычислить площадь фигуры, ограниченной линиями
![]()
Решение.
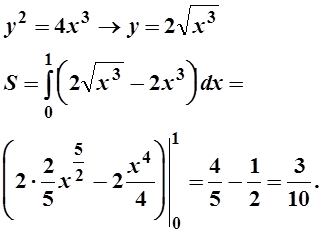
2.
Найти объем тела, образованного
вращением вокруг оси Ох фигуры, ограниченной линиями: ![]()
 |
Решение.
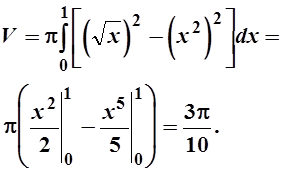
3.
Вычислить длину дуги кривой ![]() при
при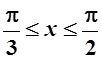 .
.
 у
у
![]()
![]()
![]()
![]()
![]()
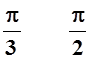
х
Решение. Найдем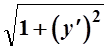 =
=
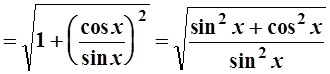
=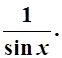
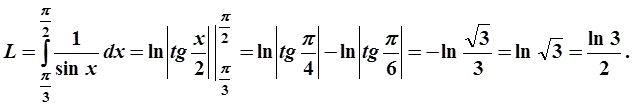
Контрольная работа 6
Тема: Дифференциальные уравнения
Задания 1, 2 (321-340). Найти общее решение дифференциаль-ного уравнения.
Указания к решению задания 1. В №№ 321-330 требуется решить дифференциальное уравнение 1-го порядка (ДУ-1). Это либо уравнения с разделяющимися переменными, либо однородные, либо линейные. Сначала следует проверить, является ли ДУ-1 уравнением с разделяющимися переменными, то есть нельзя ли представить его в виде: y¢=f(x)×g(x). Если это возможно, то уравнение записывается в разделенной форме
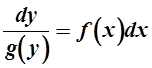
и затем интегрируется каждая часть равенства отдельно.
Если уравнение не является уравнением с разделяющимися переменными, то надо проверить, не будет ли оно однородным. Для этого надо записать ДУ-1 в виде y¢=f(x, y) и затем в правую часть равенства вместо х подставить tx, а вместо у подставить ty. Если при этом t сократится, то есть получится f(tx, ty)=f(x, y), то уравнение является однородным. В этом случае производят замену
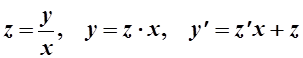 , после
чего ДУ-1 становится уравнением с разделяющимися переменными относительно новой
функции z=z(x) . Это уравнение решают, а затем производят
обратную замену.
, после
чего ДУ-1 становится уравнением с разделяющимися переменными относительно новой
функции z=z(x) . Это уравнение решают, а затем производят
обратную замену.
Если в ДУ-1 y¢и у входят в первой степени и между собой не перемножаются, то такое уравнение называется линейным. Его можно записать в виде y¢+p(x)y=q(x) . Для решения этого уравнения функцию у представляют как произведение функций y=u×v , которые определятся из решения следующей системы ДУ-1
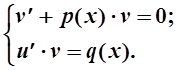
Каждое из этих уравнений является ДУ-1 с разделяющимися переменными. Сначала из первого уравнения находим v , затем, подставляя v , без учета произвольной постоянной во второе уравнение находим u .
Примеры : 1. 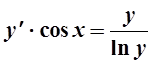 .
.
Решение. Это уравнение является уравнением с разделяющимися переменными:
![]()
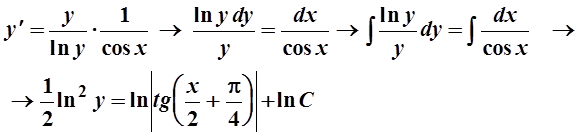
Ответ: 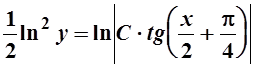 .
.
2. 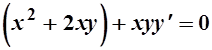
Разрешим относительно у¢: 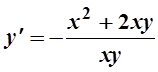 .
.
Это уравнение не является уравнением с разделяющимися перемен-ными. Проверим его на однородность:
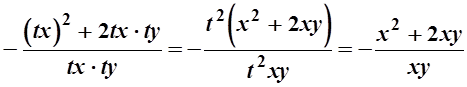 .
.
Условие однородности выполнено, поэтому подставляем в уравнение замену 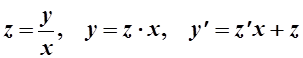 .
.
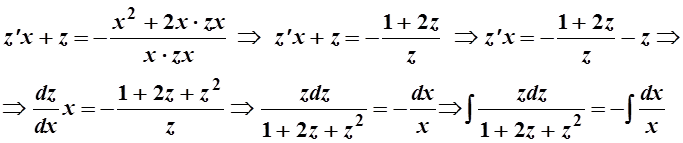
Вычислим первый интеграл
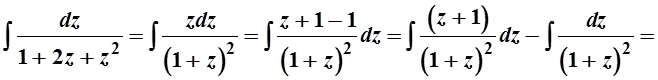
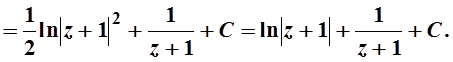
Приравняем полученное выражение к интегралу от правой части уравнения 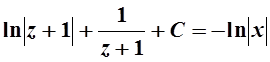 . Возвращаемся к искомой функции у:
. Возвращаемся к искомой функции у:
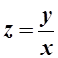
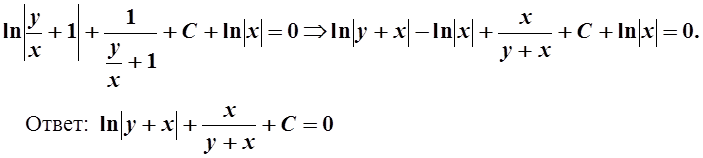
3. ![]()
Видно, что у и у¢входят в уравнение в первой степени, поэтому уравнение - линейное. Делаем замену y=u×v, y¢=u¢×v+u×v¢. Тогда получаем
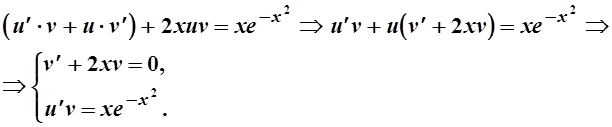
Решаем первое уравнение
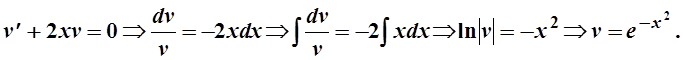
Подставляем во второе
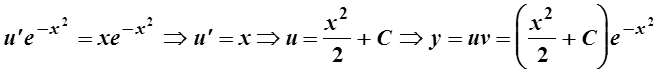
Ответ: 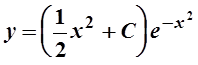
Указания к решению задачи 2. В №№ 331-346 для решения предлагаются дифференциальные уравнения 2-го порядка (ДУ-2): F(x, y, y¢, y² )=0, которые допускают понижение порядка, что позволяет свести их к решению двух ДУ-1. При этом имеют место два случая :
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.