Указания к решению. При решении физической задачи необходимо использовать какой либо физический закон. В задачах №№361-364 таким законом является второй закон Ньютона: F=a×m. В задаче №365 для составления ДУ надо рассмотреть изменение концентрации раствора за промежуток Dt .В задачах № 366-370 необходимо использовать уравнение касательной к кривой y=f(x) в точке М(х,у):
Y-y=y¢(x) (X-x),
Где Y и Х – текущие координаты касательной, а (х, у) –текущая точка кривой y=f(x).
Пример. 1. Моторная лодка движется в спокойной воде со скоростью v=10 км/ч. На полном ходу ее мотор был выключен и через t=20 сек скорость лодки уменьшилась до v1=6 км/ч. Считая, что сила сопротивления воды движению лодки пропорциональна ее скорости, найти скорость лодки через 2 мин после остановки.
Решение. По второму закону Ньютона F=a×m. По условию F=-kv (k- коэффициент пропорциональности), поэтому -kv=am, или
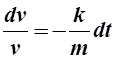. Обозначим 
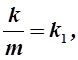тогда
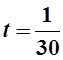ч, поэтому
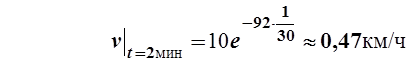
Ответ: Через 
2. Найти уравнение кривой, проходящей через точку А(0; 1) и обладающей тем свойством, что угловой коэффициент касательной в любой ее точке пропорционален ординате точки касания с коэффициентом пропорциональности k=2.
Решение. Так как у¢(х) –есть угловой коэффициент касательной а у- есть ордината точки касания, то исходя из условий задачи получаем уравнение: у¢=2у. Это уравнение есть уравнение с разделяющимися переменными, поэтому
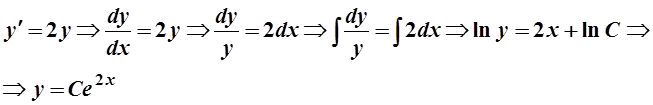
Последнее равенство есть общее решение уравнения. Подставим в него условие того, что кривая проходит через точку А (0; 1):
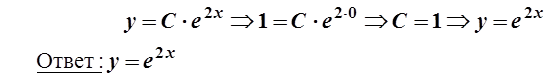
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО ВЫСШЕЙ МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ФАКУЛЬТЕТА(1 курс, 2 семестр)
1. Уравнение касательной и нормали к кривой.
2. Теорема Ролля.
3. Теорема Лагранжа.
4. Теорема Коши.
5. Правило Лопиталя.
6. Формула Тейлора.
7. Необходимые и достаточные условия возрастания и убывания функций.
8. Экстремум функции. Необходимые и достаточные условия экстремума.
9. Нахождение наибольшего и наименьшего значений функции на отрезке.
10.Выпуклость и вогнутость, точки перегиба.
11.Асимптоты кривых.
12.Первообразная и ее свойства.
13.Неопределенный интеграл и его свойства.
14.Таблица интегралов.
15.Интегрирование по частям.
16.Интегрирование подстановкой.
17.Интегрирование рациональных функций.
18.Интегрирование тригонометрических функций.
19.Интегрирование иррациональных выражений.
20.Определенный интеграл и его свойства.
21.Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
22.Вычисление определенных интегралов методом по частям.
23.Вычисление определенных интегралов методом подстановкой.
24.Приближенное вычисление определенного интеграла: формулы прямоугольников, трапеций, Симпсона.
25.Вычисление площадей плоских фигур в декартовых координатах.
26.Вычисление объемов тел вращения.
27.Вычисление длин дуг кривых.
28.Вычисление площади поверхности тела вращения.
29.Несобственные интегралы I-го рода.
30.Несобственные интегралы П-го рода.
31.ДУ-1. Общее и частное решения. Задача Коши.
32.ДУ-1 с разделяющимися переменными.
33.Однородные ДУ-1.
34.Линейные ДУ-1.
35.ДУ-2. Общее и частное решения. Задача Коши.
36.ДУ-2, допускающие понижение порядка.
37.ЛОДУ-2. Структура общего решения. Фундаментальная система решений.
38.Экспоненциальный метод решения ЛОДУ-2 с постоянными коэффициентами.
39.ЛНДУ-2. Теорема о структуре общего решения.
40.ЛНДУ-2 с постоянными коэффициентами и специальной правой частью.
41.Метод вариации произвольных постоянных для решения ЛНДУ-2.
42.Нормальная СДУ. Задача Коши.
43.Решение нормальной СДУ с постоянными коэффициентами с помощью характеристического уравнения.
СПИСОК ЛИТЕРАТУРЫ
1. Шипачев В.С. Высшая математика. М., Высшая школа,1985.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т.1, Т.2, М., Высшая школа. 1980.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление.
Т.1, Т.2, М., Наука, 1970.
Составитель
Сергей Андреевич Лактионов
РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ
РАБОТ ПО КУРСУ «ВЫСШАЯ МАТЕМАТИКА»
2 семестр для студентов-заочников
Утверждены на заседании кафедры высшей математики
15 декабря 1998 г., протокол № 283 и одобрены редакционной комиссией факультета
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.