-1 0
Из рисунка следует, что на ![]() функция убывает, а на
интервале
функция убывает, а на
интервале ![]() - возрастает. Точка х=0
является точкой локального минимума, уmin(0)=1.
- возрастает. Точка х=0
является точкой локального минимума, уmin(0)=1.
6.
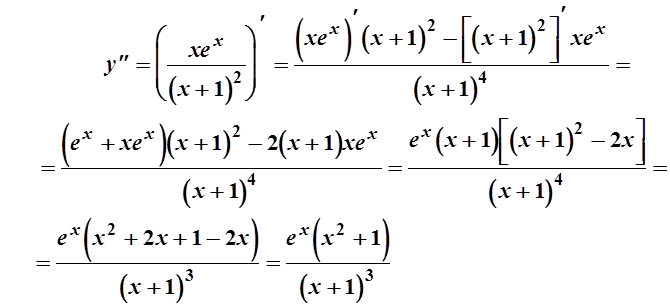
![]() при любом х ;
при любом х ;![]() не определена при х=-1.
Исследуем знак
не определена при х=-1.
Исследуем знак ![]()
 |
|||
|
|||
Поэтому
на интервале ![]() график выпуклый, а на интервале
график выпуклый, а на интервале ![]() - вогнутый. Точек перегиба нет.
- вогнутый. Точек перегиба нет.
7. Определим еще несколько дополнительных точек графика
х |
-4 |
-2 |
-1,5 |
-0,5 |
1 |
3 |
у |
-0,006 |
-0,13 |
-0,4 |
1,2 |
1,3 |
5 |
Исходя из полученных данных строим график.
 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Контрольная работа 5
Контрольная работа 5
Тема: Неопределенный и определенный интегралы.
Задание 1. (281-290) Найти неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием.
Указания к решению. В п. а) следует использовать прием подведения под знак дифференциала, например,
![]()
![]() , ×
, ×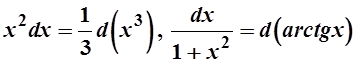 и т. д.
и т. д.
В п. б) необходимо использовать формулу интегрирования по частям ![]()
В п. в) применяется метод интегрирования рациональных дробей. Этот метод рассмотрен в примере. В п. г) применяется формула замены переменной в неопределенном интеграле:
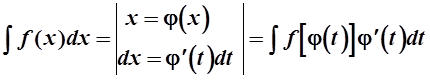
При решении задач надо использовать следующие правила интегрирования:
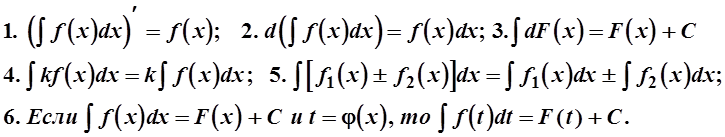
Приведем также таблицу основных интегралов:
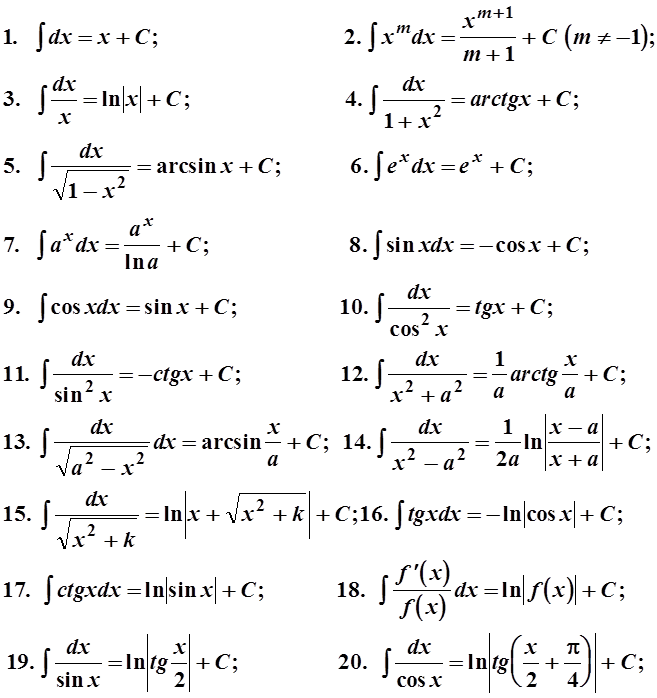
Примеры. 1. ![]() .
.
Решение.
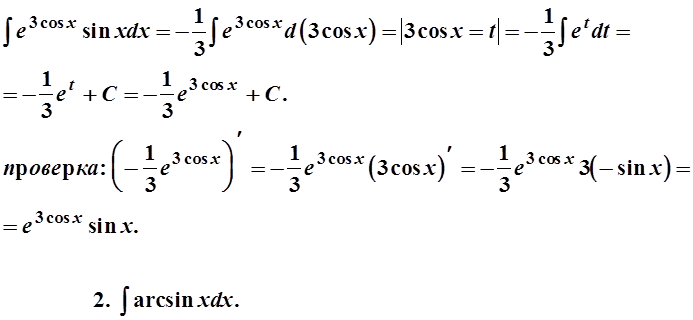 Решение
Решение
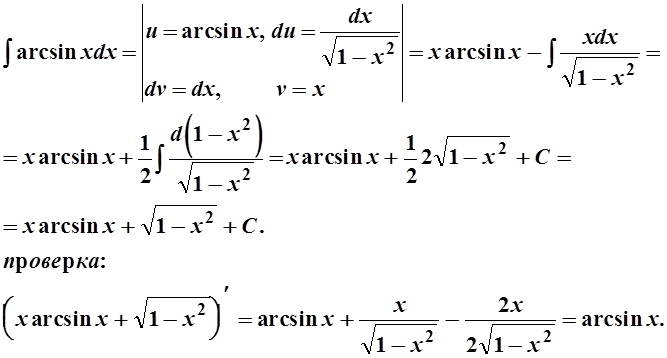
3. 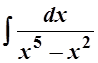 .
.
Решение. Разложим знаменатель на множители:
![]() , тогда
, тогда
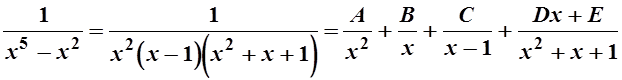 .
.
Приведем правую часть к общему знаменателю и приравняем числители левой и правой частей:
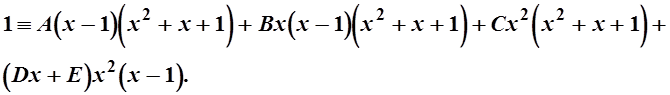 Так как х=0
и х=1 являются корнями знаменателя, то удобно придать эти
значения х в последнем равенстве.
Так как х=0
и х=1 являются корнями знаменателя, то удобно придать эти
значения х в последнем равенстве.
При х=0 имеем 1= - А , то есть А =-1.
При х=1 имеем 1=3С
, то есть С = ![]() .
.
Перепишем равенство в виде
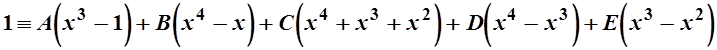 и приравняем
коэффициенты при х4, х3 и х2
в правой и левой частях равенства
и приравняем
коэффициенты при х4, х3 и х2
в правой и левой частях равенства
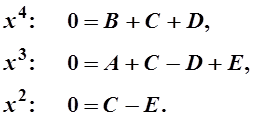
Из этой системы найдем: 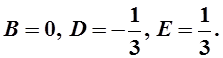 Итак
Итак
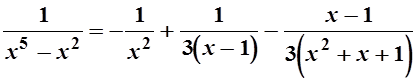
Следовательно,
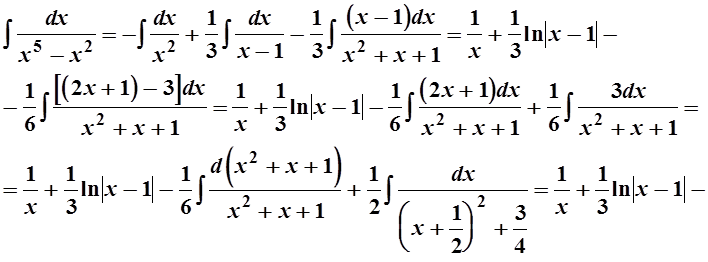
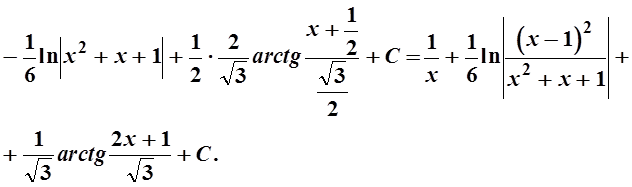
4. 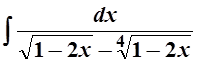
Решение. Сделаем замену ![]() , тогда
, тогда 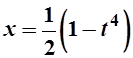 ,
,
![]() , поэтому
, поэтому
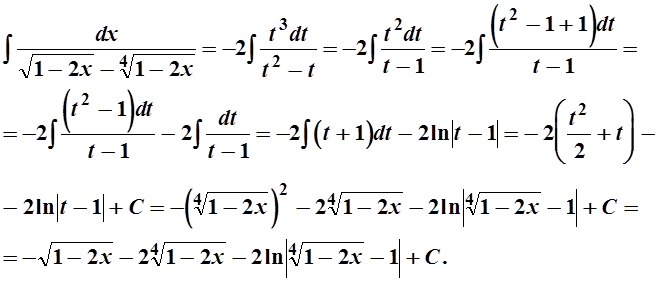
Задание 2. (301-310). Вычислить несобственный интеграл или доказать его расходимость.
Указания к решению. Несобственными интегралами I-го рода называются интегралы с бесконечными пределами. К таким интегралам относятся интегралы вида
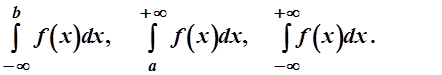
Эти интегралы вычисляются по формулам
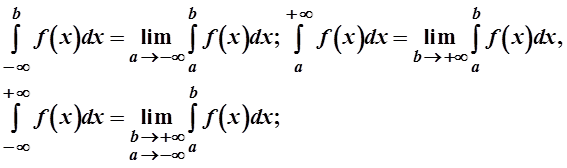
Где 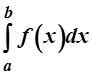 уже не является
несобственным интегралом.
уже не является
несобственным интегралом.
При этом, если пределы в правых частях формул существуют и конечны, то говорят, что соответствующие интегралы сходятся, а если пределы не существуют или бесконечны, то говорят, что интегралы расходятся.
Интеграл 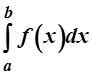 называется
несобственным интегралом П-го рода, если функция f(x) имеет
разрыв типа ¢¢бесконечность¢¢ на отрезке [a;
b]. Пусть этот разрыв происходит в точке х=с (с
может совпадать с а или b ). Тогда вычисление
интегралов происходит по формуле
называется
несобственным интегралом П-го рода, если функция f(x) имеет
разрыв типа ¢¢бесконечность¢¢ на отрезке [a;
b]. Пусть этот разрыв происходит в точке х=с (с
может совпадать с а или b ). Тогда вычисление
интегралов происходит по формуле
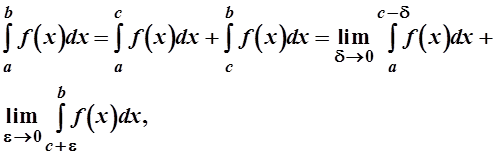
где на отрезках [a; c-d] и [c+e; b] функция f(x) является непрерывной. Если с=а, то формула примет вид
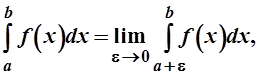
а в случае c=b вид
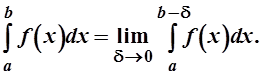
Во всех формулах e>0 и d>0. Сходимость и расходимость определяется теми же условиями, что и для несобственных интегралов I-го рода.
Примеры. 1. 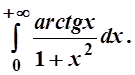
Решение .
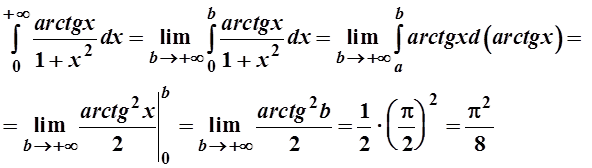
-интеграл сходится.
2.
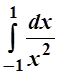 .
.
Решение. Функция 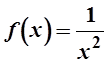 терпит бесконечный
разрыв на отрезке [-1; 1] в точке х=0, поэтому
терпит бесконечный
разрыв на отрезке [-1; 1] в точке х=0, поэтому
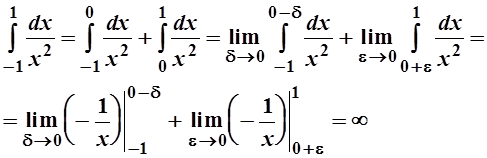
-интеграл расходится.
Задание 3. (311-320). Решить задачу на приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения или длин дуг кривых.
Указания к решению. Площадь плоской фигуры, ограниченной прямыми х=а и х=b и графиками функций
![]()
![]()
находится по формуле (см. рис.)
|
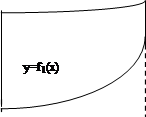 |
![]() a b х
a b х
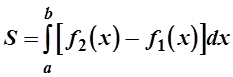
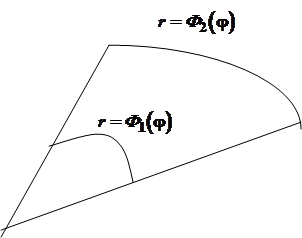
Если область задана в полярной системе координат ![]() и
ограничена кривыми
и
ограничена кривыми ![]() , а также лучами j = a и j = b,
, а также лучами j = a и j = b, ![]() , то площадь этой области находится по
формуле
, то площадь этой области находится по
формуле
 |
 b
b
![]() a
a
![]() p
p
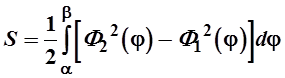
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.