Примеры и рекомендации по выполнению контрольных работ 4-6 по курсу «Высшая математика» (Приложение производной. Дифференциальные уравнения), страница 4

1) в уравнение не входит  у. В этом случае полагают   y¢=p(x), y²=p¢(x)  после чего уравнение принимает вид F(x, p, p¢)=0. Из этого уравнения определяют р, а затем из уравнения у¢=р  определяют у .

2) в уравнение не входит х. В таких уравнениях полагают у новой переменной, а у¢- функцией от нее: у¢=р(у), у²=р¢(у)×р(у). Подставляя эту замену в исходное уравнение, получаем  F(y, p, p¢p)=0. Решая это ДУ-1 находим у¢=р(у), а затем из этого уравнения определяем у=у(х).

Примеры.             1.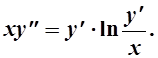

Решение. В уравнении нет у , положим у¢=р(х), у²=р¢:

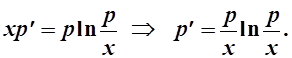
Это  уравнение  будет  однородным,  поэтому  положим  p=z×x,  p¢=z¢×x+z :

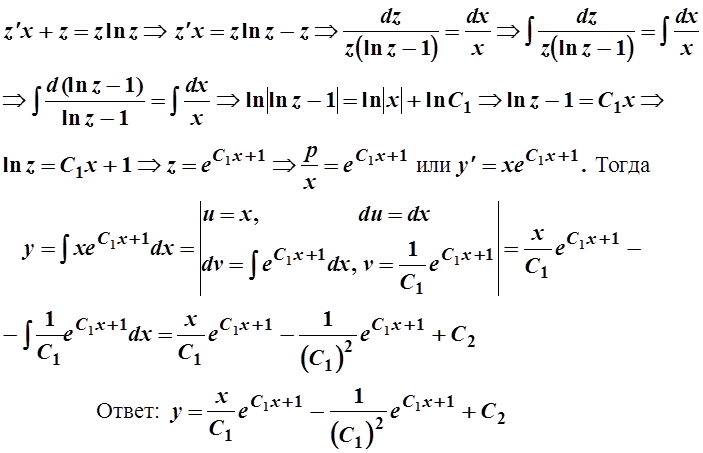
2.      уу²-(у¢)²=0

Решение. В уравнении нет х, поэтому положим у¢=р(у),  у²=р¢р, тогда, подставляя в уравнение, получаем  ур¢р-р²=0    или   р(ур¢-р)=0.

Таким образом, либо р=0 Þ у¢=0 Þ у=С (тривиальное решение), либо   ур¢-р=0, тогда

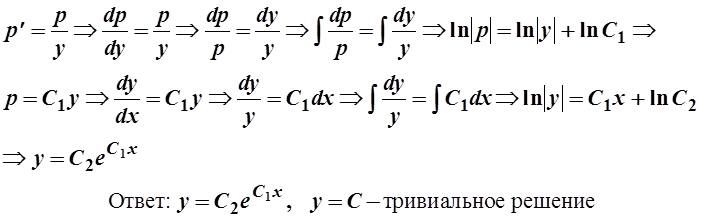
Задание 3.  (341-350). Найти частное решение дифферен-циального уравнения y²+py¢+qy=f(x) , удовлетворяющее начальным условиям у(0)=у₀, у¢(0)=у₀¢.

Указания к решению. Сначала надо найти общее решение однородного уравнения y²+py¢+qy=0. Для этого составляют характеристическое уравнение и определяют его корни по формуле: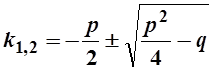.  Имеют место три случая:

1) 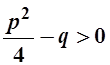, тогда корни вещественны и различны и общее решение однородного уравнения запишется в виде:

2)

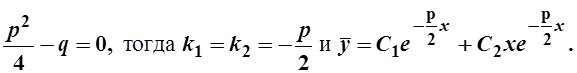
3)

  

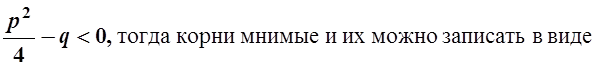
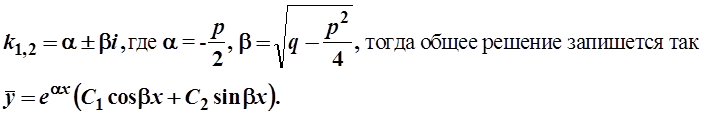
Общее решение неоднородного уравнения y²+py¢+qy=f(x) найдется как сумма   и  y* , где - общее решение однородного уравнения, а у*- частное решение неоднородного уравнения. Чтобы найти у*  необходимо представить его в виде правой части f(x)  с неопределенными коэффициентами перед функциями, домножая в силу необходимости на х, если f(x) совпадает с одной из функций в , стоящих перед С₁  и С₂  и на х² , если такое совпадение происходит дважды. Затем, подставляя y*  в уравнение, находим неопределенные коэффициенты в y* . После этого подставляем в общее решение неоднородного уравнения у= + y* заданные начальные условия и, определяя С₁  и С₂ , находим частное решение.

Пример. 

Решение. Соответствующее однородное уравнение имеет вид

Характеристическое уравнение

Правая часть  f(x)=e^4x. Эта функция совпадает дважды с функциями в , стоящими перед С₁ и С₂ , поэтому частное решение у* запишется в виде:

у*=Ае^4х×х², где А –неопределённый коэффициент. Подставим у* в уравнение

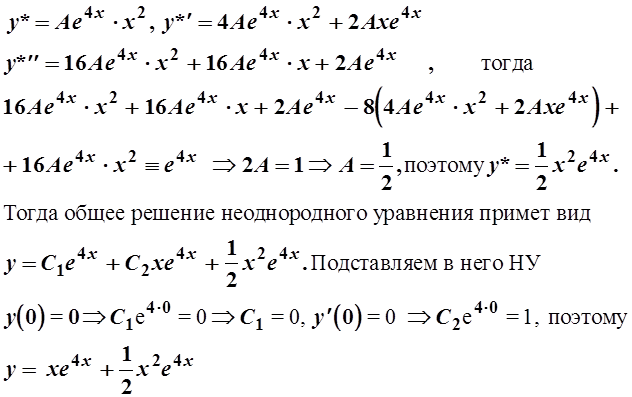
Ответ: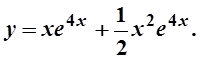

Задание 4. (351-360). Дана система линейных дифференциальных уравнений с постоянными коэффициентами

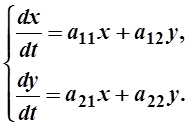                                                     (1)

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Указания к решению. Характеристическим уравнением системы (1) называется уравнение

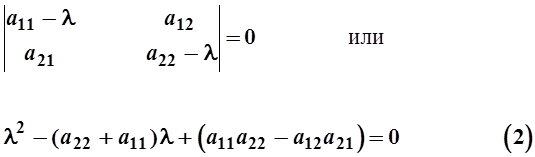
Пусть l₁ и l₂ – два различных корня уравнения (2). Составим для них системы уравнений

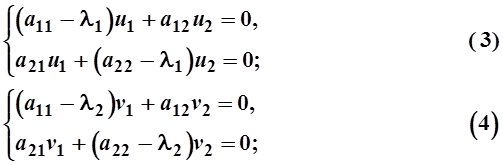
В каждой из систем одно из уравнений является следствием другого, поэтому вместо двух систем (3) и (4) получаются два уравнения, например

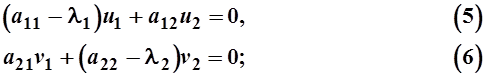
Если в (5) 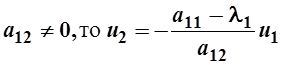, полагая u₁=1, получаем одно из решений (5) в виде 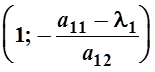 . Вектор с такими координатами является собственным вектором матрицы коэффициентов системы (1), соответствующим собственному числу l₁. Этот вектор еще можно записать в виде

Аналогично, решая уравнение (6), получаем собственный вектор

Общее решение системы  (1) запишется при этом в виде

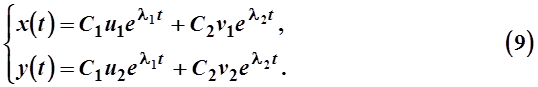
В матричной форме решение (9) запишется так:

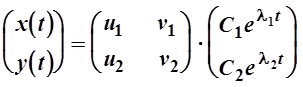
Пример.  

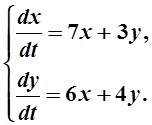
Решение.  Найдем характеристическое уравнение

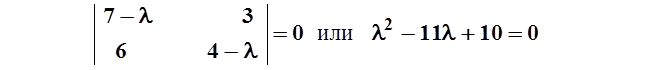
Отсюда l₁=1, l₂=10 –характеристические числа. Подставляя l₁=1  в систему (3) , получаем

  

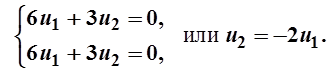
Поэтому, полагая u₁=1, в качестве собственного вектора можно взять (1; -2). При  l₂=10 из (4) получаем

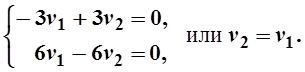
Полагая v₁=1, получаем собственный вектор (1;1). Соответствующее этим собственным векторам общее решение (9) запишется так

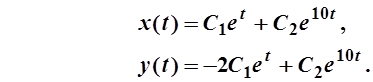
В матричной форме это можно записать так

.

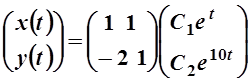Задание 5.  (361-370) Решить физическую или геометрическую задачу, используя дифференциальные уравнения.