Прежде всего
заметим, что функция определена на всей числовой оси. Найдем точки,
подозрительные на экстремум. Для этого вычислим производную: 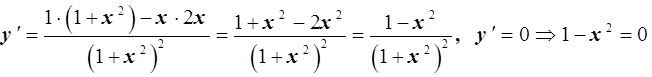
Имеем две
критические точки ![]() . Левее точки
. Левее точки ![]()
![]() , правее
, правее
![]() , значит в точке
, значит в точке ![]() функция
имеет минимум. Ясно, что в точке
функция
имеет минимум. Ясно, что в точке ![]() функция имеет максимум.
График функции изображен на рис.7.
функция имеет максимум.
График функции изображен на рис.7.
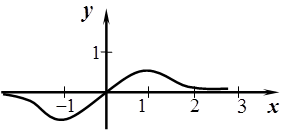 |
Рис. 7
Нетрудно
вычислить ![]() и
и ![]() .
Действительно,
.
Действительно, 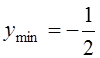 ,
, 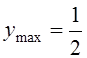 . Если учесть, что
. Если учесть, что ![]() и
и 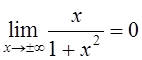 , то легко нарисовать график этой функции.
, то легко нарисовать график этой функции.
Второй достаточный признак экстремума.
Исследование функций с помощью второй производной
Теорема
. Если в окрестности точки x0 функция f (x) непрерывна и
дважды дифференцируема, причем в этой окрестности ![]() непрерывна,
а в точке x0 первая производная обращается в нуль, то если
непрерывна,
а в точке x0 первая производная обращается в нуль, то если ![]() , в точке x0 функция имеет
максимум, а если
, в точке x0 функция имеет
максимум, а если ![]() , в точке x0 функция имеет минимум.
, в точке x0 функция имеет минимум.
Доказательство. Докажем первую половину теоремы.
Пусть ![]()
Так как по условию теоремы ![]() непрерывна в некоторой d окрестности точки
непрерывна в некоторой d окрестности точки ![]() , то найдется некоторый малый отрезок,
окружающий точку
, то найдется некоторый малый отрезок,
окружающий точку ![]() , во всех точках которого
, во всех точках которого ![]()
Но по определению второй производной ![]() и
и ![]() ,
откуда следует монотонное убывание на этом отрезке функции
,
откуда следует монотонное убывание на этом отрезке функции ![]()
Так как по условию теоремы ![]() , то при
, то при ![]()
![]() , а при
, а при ![]()
![]() , т.е. производная
, т.е. производная ![]() меняет
знак с «+» на «-» при переходе через точку
меняет
знак с «+» на «-» при переходе через точку ![]() и в этой
точке согласно предыдущей теоремы функция
и в этой
точке согласно предыдущей теоремы функция ![]() достигает
максимума.
достигает
максимума.
Вторая часть теоремы доказывается аналогично.
Выпуклость и вогнутость кривых
Определение 1. Будем говорить, что непрерывная кривая на промежутке [a; b], выпукла вверх, или просто выпукла, если график располагается ниже касательной к графику функции, проведенной через любую точку графика (рис. 8а).
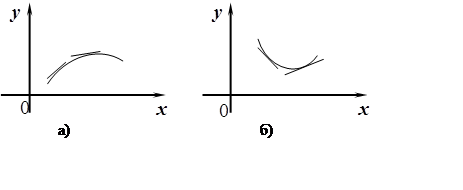 |
Рис. 8.
Определение 2. Будем говорить, что непрерывная кривая на промежутке [a; b], выпукла вниз, или вогнута, если ее график располагается выше касательной к графику функции, проведенной через любую точку графика (рис.8б).
Теорема. Если функция f (x) дважды дифференцируема на промежутке [a; b], причем ![]() на этом
промежутке, то на промежутке [a; b], график функции выпуклый, а если
на этом
промежутке, то на промежутке [a; b], график функции выпуклый, а если ![]() , то на промежутке [a; b], график функции вогнутый.
, то на промежутке [a; b], график функции вогнутый.
Доказательство. Пусть ![]()
Проведем в точке ![]() касательную
Т к графику функции. По условию теоремы необходимо доказать, что все точки
графика функции лежат выше касательной, т.е. ординаты любой точки кривой
касательную
Т к графику функции. По условию теоремы необходимо доказать, что все точки
графика функции лежат выше касательной, т.е. ординаты любой точки кривой ![]() больше ординаты
больше ординаты ![]() касательной
при том же значении аргумента.
касательной
при том же значении аргумента.
Уравнение касательной к кривой ![]() в точке
в точке ![]() имеет
вид:
имеет
вид:
![]() , откуда
, откуда ![]() ,
где
,
где ![]() - ординаты точек касательной.
- ординаты точек касательной.
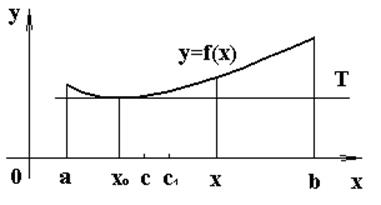
Рис. 9.
Разность ординат точек кривой и касательной ![]()
Применим теорему Лагранжа к функции ![]() на отрезке
на отрезке ![]() :
:
![]() , и тогда
, и тогда ![]()
![]() , или
, или ![]() , где
, где ![]()
![]()
![]() .
.
Применим
теперь теорему Лагранжа к функции ![]() на
на ![]() :
:
![]() , где
, где ![]()
![]()
![]() .
.
В
последнем равенстве ![]() а
а 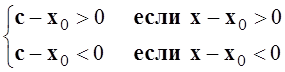 .
.
Следовательно,
![]() , т.е. ординаты точек кривой больше ординат
точек касательной при одной и той же абсциссе.
, т.е. ординаты точек кривой больше ординат
точек касательной при одной и той же абсциссе.
Значит,
график функции ![]() на
на ![]() -
вогнутый(см. рис.9).
-
вогнутый(см. рис.9).
Доказательство
выпуклости графика функции на ![]() проводится аналогично.
проводится аналогично.
Точки перегиба
Точка на графике
функции f (x), отделяющая выпуклую часть графика от вогнутой,
называется точкой перегиба. Из определения следует, что при прохождении через
точку перегиба вторая производная меняет знак. Если x0 – абсцисса точки перегиба, то ![]() ,
или
,
или ![]() , или
, или ![]() не
существует.
не
существует.
Пример. Найдем интервалы выпуклости и вогнутости и точки перегиба функции y = x³ -6x² + x – 12.
y′ = 3x² - 12x + 1, y′′ = 6x – 12.
y′′ = 0 при х = 2, y′′ < 0 при х < 2, y′′ > 0 при х > 2.
Таким образом, график функции является выпуклым при х < 2, вогнутым при х > 2, а х = 2 – точка его перегиба.
Наибольшее и наименьшее значение функции
 Допустим, что некоторая функция f (x) непрерывна на
промежутке [a; b], тогда на этом
промежутке она имеет наибольшее и наименьшее значения. Чтобы их найти, нужно
отыскать все максимумы и минимумы функции, вычислить ее значения на концах
промежутка, а затем сравнить их между собой и выбрать наименьшее и наибольшее.
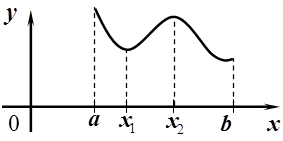
На рис.10 функция f (x) имеет наибольшее значение в точке x = a, которое больше
Допустим, что некоторая функция f (x) непрерывна на
промежутке [a; b], тогда на этом
промежутке она имеет наибольшее и наименьшее значения. Чтобы их найти, нужно
отыскать все максимумы и минимумы функции, вычислить ее значения на концах
промежутка, а затем сравнить их между собой и выбрать наименьшее и наибольшее.
На рис.10 функция f (x) имеет наибольшее значение в точке x = a, которое больше ![]() , а наименьшим значением является f (b), которое меньше
минимального значения функции
, а наименьшим значением является f (b), которое меньше
минимального значения функции ![]() .
.
Рис. 10.
Пример.
Найдем наибольшее и наименьшее значения функции y = x³ + 3x² - 9x –15 на отрезке [-4, 4].
y ′ = 3x² + 6x – 9 = 0 при х = -3 и х =1 . При этом обе найденные критические точки принадлежат данному отрезку. Вычислим значения функции при х = -4, х = -3, х = 1 и х =4.
|
х |
-4 |
-3 |
1 |
4 |
|
у |
5 |
12 |
-20 |
61 |
Таким образом, наибольшее значение функции на рассматриваемом отрезке равно 61 и принимается на его правой границе, а наименьшее равно –20 и достигается в точке минимума внутри отрезка.
Четность и нечетность функции
При исследовании
функции всегда нелишне проверить, является ли данная функция четной или
нечетной, так как в таком случае достаточно исследовать функцию только для ![]() , а затем отобразить ее для отрицательных x симметрично относительно оси 0y или симметрично относительно начала
координат.
, а затем отобразить ее для отрицательных x симметрично относительно оси 0y или симметрично относительно начала
координат.
Определение 1. Функция f (x) называется четной, если ![]() для любой точки x из области определения функции.
для любой точки x из области определения функции.
Например,
функция ![]() - четная функция; действительно,
- четная функция; действительно, ![]() .
Ясно, что график четной функции симметричен относительно оси 0y.
.
Ясно, что график четной функции симметричен относительно оси 0y.
Определение 2. Функция f (x) называется нечетной,
если ![]() .
.
Например, функция ![]() нечетная функция, так как
нечетная функция, так как ![]() , т.е.
, т.е. ![]() .
.
Ясно, что график нечетной функции симметричен относительно начала координат.
Асимптоты кривых
Определение. Прямая линия называется асимптотой
графика функции ![]() , если расстояние между текущей точкой графика и этой
прямой стремится к нулю по мере удаления точки от начала координат (рис. 2.8.5).
, если расстояние между текущей точкой графика и этой
прямой стремится к нулю по мере удаления точки от начала координат (рис. 2.8.5).
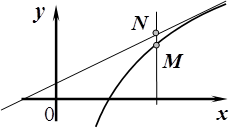 |
Рис. 11.
Итак,
предположим, что график функции имеет наклонную асимптоту ![]()
![]() , тогда очевидно, что
, тогда очевидно, что ![]() , т.е.
, т.е.
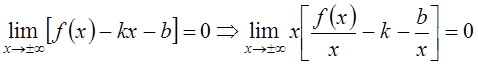 .
.
Вследствие того, что
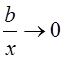 , при
, при ![]() , то
ясно, что последнее предельное равенство может иметь место, лишь когда выражение
, то
ясно, что последнее предельное равенство может иметь место, лишь когда выражение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.