Теоремы о дифференцируемых функциях. Геометрический смысл теоремы Коши. Исследование функций с помощью первой производной

Лекция 1. 10.02.03.

Теоремы о дифференцируемых функциях

1. Теорема Ролля

Теорема Ролля. Если функция f (x) непрерывна на замкнутом промежутке [a; b], в каждой точке интервала ]a; b[ существует конечная производная f '(x) и, кроме того, f (a) = f (b), то тогда между точками a и b найдется хотя бы одна точка c (a < c < b) такая, что f '(с)=0.

Доказательство. Функция f (x) непрерывна на промежутке [a; b], следовательно, на этом промежутке она принимает наименьшее значение m и наибольшее значение M.

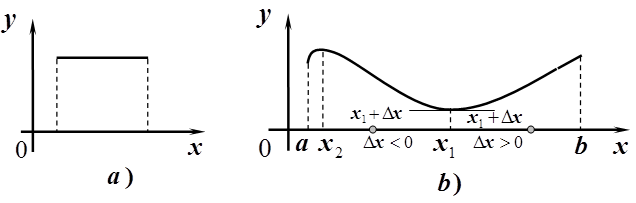Если окажется, что m = M, то f (x) постоянна на промежутке [a; b] (рис.1), т.е. f (x) = const, следовательно, f '(x) = 0, " xÎ[a; b], в частности и в некоторой точке cÎ]a; b[.

Рис.1

Если m < M, то существует точки x₁ и x₂ такие, что f (x₁) = m, f (x₂) = M, причем, если бы оказалось, что точки x₁ и x₂ находятся на концах отрезка [a; b], то мы пришли бы к первому случаю, поэтому хотя бы одна из точек x₁ или x₂ лежит внутри промежутка [a; b]. Пусть для определенности a < x₁ < b и f(x₁) = m. Тогда при любом достаточно малом по модулю Dx будет f (x₁+Dx) > f (x₁), откуда следует, что 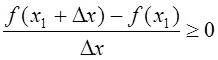 при Dx > 0;  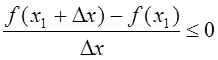при Dx < 0. Устремим теперь Dx к нулю. Так как функция f (x) дифференцируема в точке x, то это значит, что предел первой дроби должен быть равен пределу второй дроби, а это может быть только 0.

Итак, нашлась точка c = x₁ такая, что f '(c) = 0 (рис. 1).

Для точки x₂, в которой функция достигает наибольшего значения, доказательство аналогично.

Геометрический смысл теоремы Ролля

Если выполнены условия теоремы Ролля, то в некоторой точке x = c f '(c) = 0, а это означает, что касательная к графику функции y = f (x) в точке x = c параллельна оси 0x.

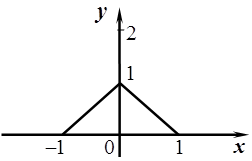Рис. 2

 Заметим, что если хотя бы в одной точке промежутка [a; b] функция не дифференцируема, то производная функции f (x) может в нуль и не обратиться (см. рис. 2). Например, функция y =1-½x½непрерывна на промежутке [-1; +1], дифференцируема на ]-1;+1[ за исключением точки x₀ = 0, причем  f(-1) = f(1) = 0, т.е. условие теоремы Ролля нарушено в единственной точке x₀ = 0 (в ней функция не дифференцируется). Очевидно, что ни в одной точке графика функции на промежутке [-1; 1] касательная       к графику не параллельна оси 0x.

2. Теорема Лагранжа

Теорема Лагранжа. Если функция y = f (x) непрерывна на замкнутом промежутке [a; b] и дифференцируема на интервале ]a; b[, то внутри промежутка [a; b] найдется хотя бы одна точка c (a < c < b) такая, что будет иметь место равенство

f (b)-f (a) = f '(c)(b - a)

– формула конечных приращений Лагранжа.

Доказательство. Введем в рассмотрение вспомогательную функцию Φ(x) = [f (x) - f (a)](b - a) - [f (b) - f (a)](x - a). Функция Φ(x) непрерывна на промежутке [a; b] как сложная функция непрерывных функций; кроме того, она дифференцируема на интервале ]a; b[, причем, Φ(a) = Φ(b) = 0. Следовательно, функция Φ(x) удовлетворяет условиям теоремы Ролля; значит, найдется точка c, лежащая внутри промежутка [a; b] такая, что Φ'(c) = 0.

Найдем Φ'(x). Ясно, что Φ'(x) = f '(x) × (b - a) - (f (b) - f (a)). Предположив здесь x = c, получим Φ'(c) = f '(c) × (b- a) - (f (b) - f (a)) = 0. Отсюда следует, что

f (b) - f (a) = f '(c) × (b - a).

Формулу конечных приращений Лагранжа можно записать несколько иначе, если положить b = x + Dx, a = x и обозначить c = x + q × Dx, где q – некоторое число, удовлетворяющее неравенству 0 < q < 1. А именно: формула Лагранжа будет иметь вид 

f (x + Dx) - f (x) = f '(x + q × Dx) × Dx     (0 < q < 1).

Геометрический смысл теоремы Лагранжа (рис. 3)

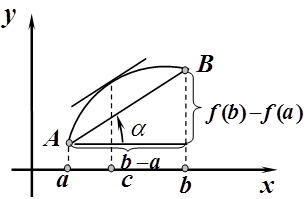Рис. 3

Итак, пусть выполнены условия теоремы Лагранжа, тогда справедлива формула конечных приращений Лагранжа.

Пусть точки A и B, лежащие на графике функции, имеют координаты A (a; f(a)), B (b; f (b)), тогда очевидно, что величина дроби 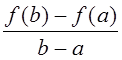 равна  тангенсу  угла  наклона  хорды  AB к  оси  0x,  т.е. .

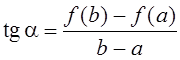С другой стороны, f '(c) = tga. Значит, в точке x = c касательная к графику функции y = f (x) параллельна хорде, стягивающей дугу кривой AB. В этом и заключается геометрический смысл теоремы Лагранжа.

3. Теорема Коши

Теорема Коши. Если на промежутке [a; b] функции j (x) и y (x) непрерывны и дифференцируемы в каждой точке интервала