Двухдвигательный электропривод передвижения мостового крана по системе ТП – ДПТ НВ, страница 8

Торможение при перемещении пустого крана.

На интервале времени t в пределах  угловая скорость и электромагнитный момент определяются соответственно:

,         (10.34)

          ,                          (10.35)

t=1 с,  тогда 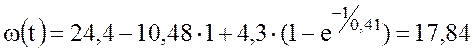   рад/с,

                        M(t)=28,15 – 23,16∙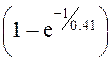=7,02 Н∙м

Таблица 10.6 – Значения ,

при торможении крана без груза.

t, с	M, Н∙м	, с-1	,Вт
0,00	28,15	24,40	534,59
0,20	19,22	23,96	455,32
0,40	13,74	22,89	420,40
0,60	10,37	21,42	403,65
0,80	8,29	19,70	394,71
1,00	7,02	17,84	389,35
1,20	6,24	15,89	385,79
1,40	5,76	13,89	383,24
1,60	5,46	11,85	381,32
1,80	5,28	9,78	379,86
2,00	5,17	7,71	378,74
2,20	5,10	5,62	377,92
2,40	5,06	3,54	377,37
2,50	5,04	2,49	377,19
2,60	5,03	1,44	377,07
2,70	5,02	0,40	377,00

    
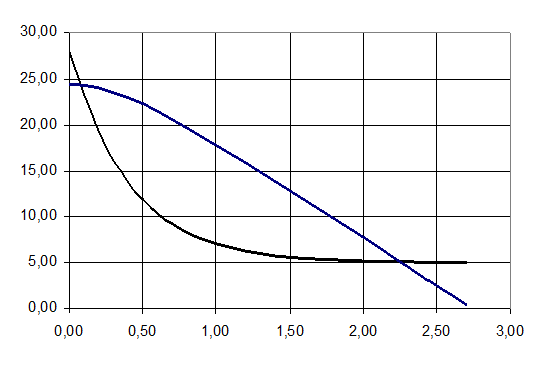
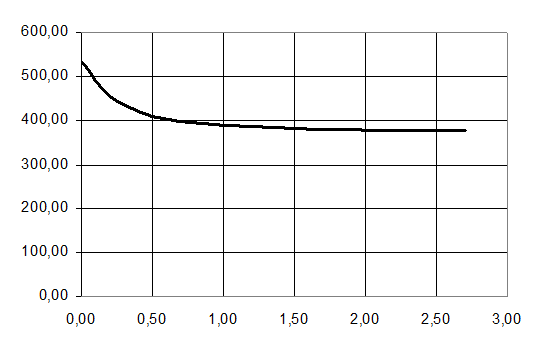
Рисунок 10.6 –Торможение при движении крана без груза.

10.3 Построение графиков переходных процессов

Потери мощности находим по формуле:

ΔP= ΔP_пост+ ΔP_пер;                                           (10.36)

Постоянные потери мощности находим по формуле:

ΔP_пост= ΔP_в+( ΔP_мх+ ΔP_ст)_ном(ω/ω_ном)²,                        (10.37)

где: - ΔP_в  - потери возбуждения:

ΔP_в=U∙I_в= U∙U/R_в =220²/130=372,3 Вт,             (10.38)

- ( ΔP_мх+ ΔP_ст)_ном – потери механические и в стали номинальные, которые находятся по формуле:

(ΔP_мх+ ΔP_ст)_ном= ΔP_{пост.ном} – ΔP_в =677 – 373,3=304,7 Вт,      (10.39)

Постоянные номинальные потери мощности:

ΔP_{пост.ном}= ΔP_ном – ΔP_{пер.ном}=1260 - 583=677 Вт,            (10.40)

ΔP_ном=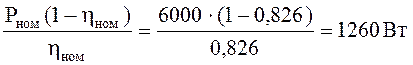,          (10.41)

Переменные номинальные потери мощности:

ΔP_{пер.ном}=I²_я.ном∙R_я=31,3²∙0,595=583 Вт,                       (10.42)

Номинальный ток якоря находим как:

I_я.ном= I_ном -I_в= I_ном-(=33 - (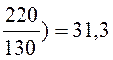 А,                (10.43)

Переменные потери мощности находим по формуле:

ΔP_пер=M²/β=М²/5,37,                                           (10.44)

Получим:  

ΔP_пост = ΔP_в +( ΔP_мх+ ΔP_ст)_ном(ω/ω_ном)²=372,3+304,7(ω/111) ²,

Тогда общая формула, по которой будем вычислять потери мощности , будет иметь вид:

ΔP= ΔP_пост+ ΔP_пер=372,3+304,7(ω/111) ²+ М²/5,37,

Теперь в эту формулу будем подставлять значения момента и угловой скорости, соответствующие определённому промежутку времени. Все данные и графики переходных процессов, полученные в результате этих расчётов для каждого из этапов переходных процессов, представлены в таблицах и на рисунках 10.1 – 10.6. 

Например, на этапе пуска крана с номинальным грузом, для t=1 с, получим:

ΔP= ΔP_пост+ ΔP_пер=372,3+304,7(0,23/111) ²+ 55,02²/5,37=936,04 Вт,

11 Окончательная проверка двигателя по нагреву и перегрузочной способности

В результате расчета переходных процессов и потерь мощности за цикл мы построили зависимости . Эти зависимости позволяют провести окончательную проверку двигателя по нагреву и перегрузочной способности.

Проверка по нагреву проводится методом средних потерь или эквивалентных величин.

В системах привода ТП – ДПТ, можно применить проверку выбранного двигателя методом эквивалентного момента, т. к. Ф=const и I пропорционален М.

Площадь под сложной кривой момента заменяется суммой площадей эквивалентных прямоугольников.

Эквивалентное значение момента:

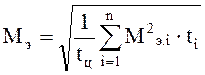,                                            (11.1)

где    - эквивалентное значение момента на i-ом интервале кривой.

Эквивалентное значение момента для трапеции:

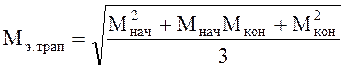,                              (11.2)

Эквивалентное значение момента для треугольника:

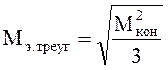,                                        (11.3)

Эквивалентное значение момента для прямоугольника:

,                                            (11.4)

В соответствии с формулами (11.2), (11.3), (11.4) и графиками получены следующие эквивалентные моменты.