Исследование переходных процессов и качества регулирования САУ. Исследование устойчивости САУ

2.  ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА РЕГУЛИРОВАНИЯ САУ

Переходные процессы и качество САУ

Устойчивость системы автоматического управления − необходимое, но далеко не достаточное условие, обеспечивающее высокое качество регулирования. Синтез систем управления должен осуществляться с учетом требований высоких показателей качества управления, достаточно хороших переходных процессов. Поэтому при исследовании САУ возникает задача расчета переходных процессов. Для этой цели используются аналитические (графо-аналитические) методы и моделирование.

Рассматривается задача построения переходных процессов аналитическими методами и моделированием, устанавливается связь между видом логарифмических частотных характеристик и характером переходных процессов.

Исследуем переходные процессы в системе стабилизации угла крена ЛА, которая задается следующей системой уравнений:

                                                            1) ;

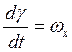                                                  2)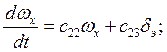                                                (3.1)

                                                            3)

где  − угол крена;  − угловая скорость крена; − угол отклонения рулей элеронов;  − заданное значение угла крена;  и   − передаточные числа контура стабилизации крена, ,  − динамические коэффициенты, определяемые формулами:

, ;

,

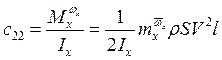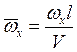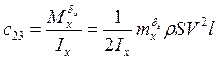где  − момент инерции ЛА относительно оси X, ,  − аэродинамические коэффициенты. Остальные обозначения в последних формулах описаны в 1-ой главе.

В (3.1) первое и второе уравнения - уравнения объекта регулирования, третье - уравнение систем управления. В системе (3.1) пренебрегают инерционностью  рулевой машинки и запаздыванием в рулевом тракте.

 Передаточная функция ЛА, характеризующая передачу воздействия от входа   до выхода  , имеет вид:

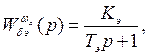                                                    (3.2)

где 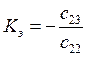  − коэффициент усиления ЛА; по движению крена 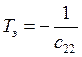− постоянная времени ЛА, характеризующая быстроту протекания переходного процесса. Численные значения коэффициентов приведены табл.3.1.

 Т а б л и ц а  3.1

Вари­анты					Вари­анты
I	-1,9	3,9	I	I	11	-2,3	14	I	1,5
2	-1,8	4,0	I	I	12	-2,5	15	I	1,5
3	-2,5	22	I	I	13	-2,7	12	I	1,5
4	-3,0	18	I	I	14	-3,0	14	I	0,8
5	-5,0	25	I	I	15	-0,8	6	0,6	0,9
6	-4,0	20	0,8	1,2	16	-5,0	22	0,8	1
7	-0,5	5	0,8	1,2	17	-3,2	19	0,5	1
8	-3,0	22	0,8	1,2	18	-3,5	20	0,8	1,2
9	-3,0	20	0,8	1,2	19	-3,0	21	0,7	1,5
10	-1,5	4	0,8	1,2	20	-2,0	5	1,1	1

Ставится задача исследовать переходные процессы в системе (3.1) при отработке заданного значения угла крена.

Весовые функции и частотные характеристики.

Динамика большого класса систем автоматического регулирования описывается системами дифференциальных уравнений с постоянными коэффициентами. С помощью такой математической модели может исследоваться и динамика  управляемого ЛА на участках полета, когда применимы метод линеаризации и приём «замораживания» параметров ЛА (параметры ЛА считаются постоянными, равными их средним значениям на рассматриваемом участке полета).

Основными характеристиками линейных стационарных динамических систем являются весовые функции и частотные характеристики. С помощью этих показателей могут решаться задачи анализа устойчивости и точности САУ при неслучайных и случайных воздействиях, а также задачи синтеза САУ.

          Весовые функции и частотные характеристики рассчитываются аналитическими  и экспериментальными методами. Экспериментальные методы имеют определённые преимущества перед аналитическими, если динамическая система описывается системой дифференциальных уравнений высокого порядка. Кроме того, экспериментальные методы применимы для исследования полунатуральной модели динамической системы, включающей в себя ЭВМ и элементы реальной аппаратуры.

           В е с о в о й  функцией   или   и м п у л ь с  н о й   п е р е х о д н о й  функцией динамической системы, имеющей один вход и один выход, называется реакция системы в момент  на единичный импульс, действующий на систему в момент :

,                                                     (1.15)

где  − весовая функция;  − оператор динамической системы, преобразующий функцию времени  на входе системы в реакцию системы;  − импульсная -функция.

Импульсная  – функция (Дельта-функция Дирака) определяется следующим образом:

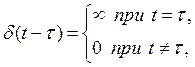                                                                                                      (1.16)

при этом 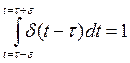 при любом .

          Имеет место, следующее фильтрующее свойство  – функции:

,        .

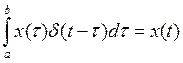Если импульс приложен в начале координат, то  и . Так как 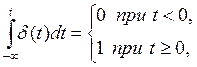, то можно записать 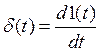. Можно показать, что -функция является четной функцией: .

Весовая функция может быть получена моделированием, если на вход системы подать -функцию.  Весовая функция удовлетворяет условию физической возможности:

                                       при                                                                 (1.17)

Это условие отражает тот факт, что любая физическая система может реагировать в момент  только на воздействия, приложенные к системе до этого момента времени, т.е. при . Для стационарных систем весовая функция зависит только от разности аргументов :

                                             .                                                                  (1.18)