Исследование переходных процессов и качества регулирования САУ. Исследование устойчивости САУ, страница 6

Для заданных значений параметров системы (2.7) требуется исследовать устойчивость системы стабилизации  угла рыскания с помощью критерия Гурвица.

Передаточная функция ЛА равна:

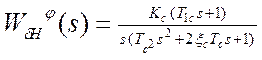                                       .                                                      (4.9)

Характеристическое уравнение системы (2.7) определяется уравнением

                                             .                                                          (4.10)            

После подстановки (2.9) в (2.10) характеристическое уравнение приводится к виду:

                                           ,                                                           (4.11)                        

где

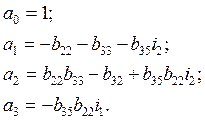                                                                                                                               (4.12)                                                             

    

Кроме определения устойчивости по критерию Гурвица,  исследуется устойчивость системы стабилизации угла рыскания моделированием. САУ устойчива, если параметры , ,  в переходном процессе отработки начальных условий затухают.

При моделировании система дифференциальных уравнений (2.7) решается методом Рунге-Кутта.

       Система уравнений (2.7) решается при  и при начальных условиях: , ; . По результатам моделирования строятся таблица и соответствующие графики функций , , .

4.3 Исследование устойчивости по критерию Михайлова.

Требуется исследовать устойчивость системы стабилизации угла рыскания по критерию Михайлова. Параметры системы (2.7) остаются без изменения, за исключением коэффициента b₃₂, который принимается равным , и коэффициента , который принимается равным нулю, т.е. . Для определения устойчивости по критерию Михайлова записывается характеристический полином

                                 .                                                              (4.13)

       Вместо  подставляется в (2.13)  и определяется вектор

                                    ,                                                                      (4.14)

где в нашем случае

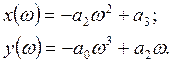                                                                                                            (4.15)

По формулам (2.15) на плоскости x, y строится годограф Михайлова, для чего  изменяется от 0 до , и делается вывод об устойчивости системы.

4.4 Исследование устойчивости по критерию Найквиста.

Требуется исследовать устойчивость САУ угла рыскания по критерию Найквиста. Параметры системы (4.7) принимаются такими же,  как и при решении задачи 4.1.

Исследование проводится при двух значениях коэффициента  . Для исследования устойчивости по критерию Найквиста определяется передаточная функция разомкнутой САУ:    

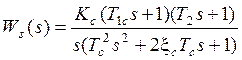                                        ,                                                      (4.16)

где                              

                   ;                         

                  

                  

                  

                    .

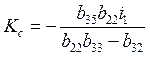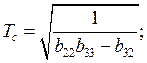
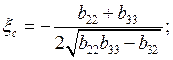
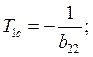
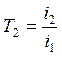Частотная характеристика разомкнутой САУ имеет вид:

                                                                                                    (4.17)

где

                  

                    .

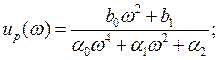
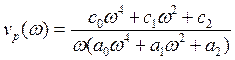Здесь

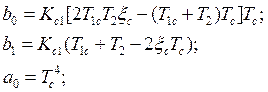                                                                                           (4.18)

                  

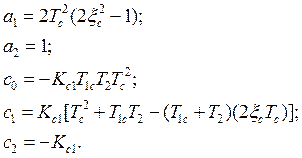
Результаты вычислений заносятся в таблицу: , .

По ее данным строится график амплитудно-фазовой характеристики разомкнутой САУ на плоскости ,  и делается вывод об устойчивости системы.

4.5 Построение области устойчивости в плоскости передаточных чисел автопилотаи   .

Характеристическое уравнение (2.11) системы стабилизации угларыскания имеет вид

                     ,                (4.19)

уравнение особой прямой определяется соотношением

                                                   .                                                                        (4.20)                                                     

Для построения границ области устойчивости в уравнение (2.19) подставим

                               (4.21)

Приравнивая нулю вещественную и мнимую части в (2.21), получим

два уравнения для определения     и  :

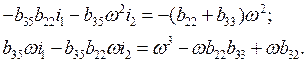                                                           (4.22)                                                              

Для решения этой системы воспользуемся правилом определителей. Определитель системы равен:

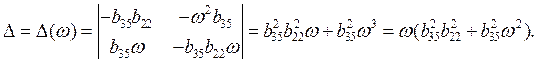                                      (4.23)

0пределители,  соответствующие     и  ,   равны:

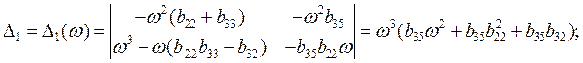                             (4.24)

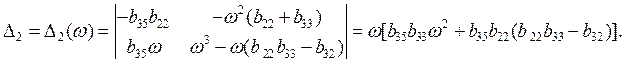                     (4.25)

Решение системы (4.22) имеет вид

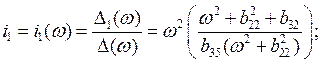                                                                                 (4.26)

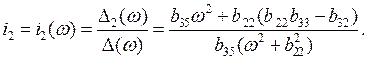                                                                        (4.27)

Уравнения (4.26) и (4.27) представляют собой уравнения D – кривой  в параметрической форме. Для построения D – кривой параметр    изменяется от  до  .

D - кривая штрихуется слева при увеличении  , если определитель системы    больше 0, и справа, если определитель    меньше  0. При этом ось  –  абсцисс,    –   ординат.

Результаты вычисления D-кривой записываются  в таблицу.

Область устойчивости ограничена  D-кривой, заданной урав­нениями (4.26), (4.27) и особой прямой (4.20).

Область устойчивости   может быть построена моделированием. Для этого задаются такие значения передаточных чисел   и  , при которых система находится на границе устойчивости. Далее изменяются передаточные числа    и    так, чтобы система стабилизации все время находилась на границе области устойчивости.