Исследование переходных процессов и качества регулирования САУ. Исследование устойчивости САУ, страница 4

Рассмотрим способ расчета частотных характеристик на примере системы стабилизации угла тангажа. Передаточная функция замкнутой САУ с отрицательной обратной связью определяется соотношением:

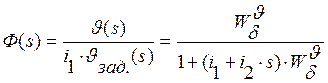                                       ,                     (1.34)

где

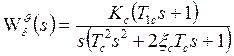                                                          .                                    (1.35)

После подстановки выражения (1.35) в (1.34) передаточная функция приводится к виду:

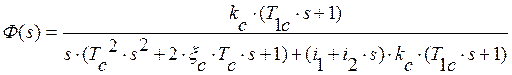                        .                  (1.36)

Для вычисления амплитудного-фазовой частотной характеристики замкнутой САУ в формулу (1.36) вместо  подставляем  и приводим частотную характеристику к виду:

                                                       ,                           (1.37)

где

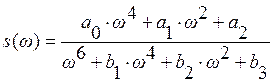                                                ;                                (1.38)

- вещественная частотная характеристика;

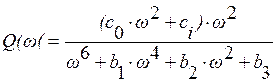                                                                      (1.39)

- мнимая частотная характеристика. Здесь

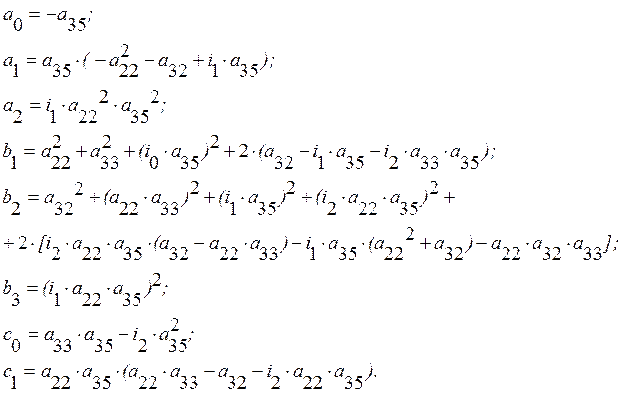          (1.40)

Амплитудная и фазовая частотные характеристики замкнутой САУ определяются с помощью выражений:

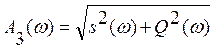                                                       ,                        (1.41)

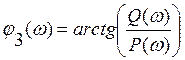                                                   .                                           (1.42)

Cтроятся графики ,  и годограф амплитудно-фазовой характеристики  замкнутой САУ. Амплитудная частотная характеристика  замкнутой САУ определяется также моделированием на ЭВМ.

При исследовании реальных систем гармоническое воздействие подается на вход системы. Рассматривается математическая модель (1.30). Для определения  моделированием воздействие  заменяется гармонической функцией

 .

Система уравнений (1.32) принимает следующий вид:

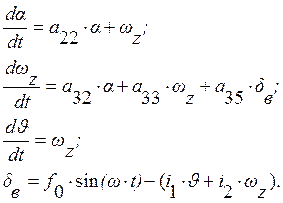                                           (1.43)     

Система (1.43) решается методом Рунге-Кутта  при десяти значениях частоты гармонических колебаний. Частота гармонических колебаний изменяется дискретно с постоянным шагом, равным начальному значению частоты колебаний , т.е.  

После окончания переходного процесса на выходе системы устанавливаются гармонические колебания с той же частотой, но с другой амплитудой и фазой. Перед началом интегрирования системы (1.43) должны быть присвоены значения следующим переменным:  − коэффициент ;  −  коэффициент ;  − коэффициент ;  − коэффициент ;  − амплитуда входного гармонического сигнала ; ОМ – начальное значение частоты гармонических колебаний  для каждой частоты  . После окончания переходного процесса на печать выводятся значения функций , ,  на интервале двух периодов колебаний.

Амплитудная характеристика

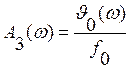                                                          (1.44)

определяется как отношение амплитуды сигнала на выходе к амплитуде сигнала на входе.

По результатам моделирования строится график . Амплитудные характеристики, рассчитанные по формуле (1.41) и полученные в результате моделирования, сравниваются.

Определение запасов устойчивости по амплитуде и фазе.

Для определения запасов устойчивости по амплитуде и фазе строятся логарифмические частотные характеристики ,  разомкнутой САУ, соответствующие ее передаточной функции:

                ,                          (1.45)

после подстановки (1.35) в (1.45) получим

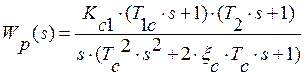     ,                               (1.46)

где ; . Логарифмическая амплитудная характеристика вычисляется по формуле:

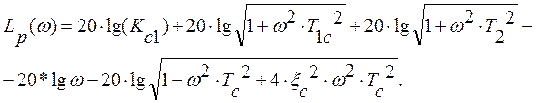                (1.47)

Фазовая частотная характеристика

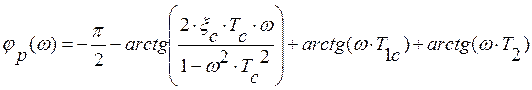.              (1.48)

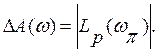В результате вычисления по формулам (1.47) и (1.48) строятся логарифмические частотные характеристики  и . Запас устойчивости по амплитуде  представляет собой абсолютную величину отрицательной ординаты ЛАХ  при частоте , при которой запаздывание по фазе достигает , т.е.

                                                                        (1.49)  

Запас устойчивости по фазе  определяется формулой

(1.50)

где  –  частота среза, т.е. частота, при которой  пересекает ось абсцисс:

.

Эта задача решается расчетным путем.

4. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ САУ.

4.1 Критерии устойчивости.

Устойчивость можно характеризовать как свойство САУ возвращаться к установившемуся состоянию после прекращения действия возмущения, которое ее из этого состояния вывело. К вопросам анализа устойчивости САУ большое практическое значение имеют общие теоремы устойчивости, сформулированные А.М.Ляпуновым. Теоремы формулируются следующим образом.

         1. Невозмущенное движение асимптотически устойчиво, если отрицательны все вещественные части корней характеристического уравнения системы, составленного для её линейного приближения.

         2. Невозмущенное движение неустойчиво, если хотя бы один корень характеристического уравнения линейного приближения имеет положительную вещественную часть. При наличии чисто мнимых корней указанного уравнения вопрос об устойчивости системы требует в каждом случае дополнительного исследования.

          Для того чтобы САУ могла нормально функционировать, она должна, прежде всего, удовлетворять требованию устойчивости. Поэтому исследование устойчивости является важной задачей ТАУ. Для суждения об ее устойчивости можно применять методы моделирования, рассматривая характер переходных процессов, а также разработанные в ТАУ критерии устойчивости.

          Рассмотрим сначала формулировки наиболее распространенных критериев: Гурвица, Михайлова и Найквиста. Критерий Гурвица является алгебраическим критерием и основан на рассмотрении характеристического уравнения замкнутой САУ. Пусть характеристическое уравнение замкнутой САУ имеет вид:

                                                    ,                                           (4.1)                                                                                              

где  – известные коэффициенты;  – порядок САУ. Критерий устойчивости Гурвица заключается в требовании положительности всех n определителей Гурвица (при ). 

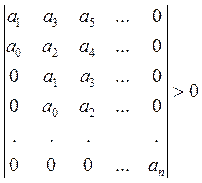                                                                                                         (4.2)                                        

        Критерий устойчивости Михайлова основан на построении кривой Михайлова, представляющей собой годограф вектора , вычерченный при изменении  от 0 до  в плоскости xy. Для устойчивости САУ -го порядка необходимо и достаточно, чтобы характеристическая  кривая Михайлова при изменении  от 0 до бесконечности, начинаясь на положительной вещественной оси, обошла последовательно в положительном направлении (против часовой стрелки) n квадрантов. При этом графики  и   для устойчивой системы пересекают ось , последовательно чередуясь, друг с другом.