Исследование переходных процессов и качества регулирования САУ. Исследование устойчивости САУ, страница 5

        Критерий Найквиста основан на рассмотрении амплитудно-фазовой характеристики     разомкнутой системы, которая однозначно связана с характеристическим уравнением замкнутой САУ:

                                                                            .                                            (4.3)

Согласно критерию Найквиста, если разомкнутая САУ устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы амплитудно-фазовая характеристика   на плоскости   не охватывала точку (-1, j0).

Если же разомкнутая  САУ неустойчива и имеет m корней в правой полуплоскости, то для устойчивости замкнутой САУ требуется, чтобы характеристика   охватывала точку (-1,j0) в положительном направлении m/2 раз при изменении   от нуля до бесконечности.

       Аналогичным образом критерий Найквиста формулируется и для логарифмических частотных характеристик. САУ устойчива, если разность между числом положительных (снизу вверх) и отрицательных (сверху вниз) переходов логарифмической фазовой характеристики  уровней -p, -3p,…равна m/2. При этом рассматриваются те диапазоны частот, для которых логарифмическая амплитудная характеристика

 больше нуля. В простейшем случае САУ будет устойчива, если частота среза  лежит левее частоты .

Другой важной задачей является построение областей устойчивости в плоскости одного или двух параметров САУ. В качестве таких параметров могут приниматься коэффициент усиления, передаточные числа системы управления. Построение областей устойчивости осуществляется при выборе параметров САУ. Построение областей устойчивости может осуществляться моделированием и аналитически с помощью метода D- разбиений.

       При графоаналитическом решении задачи исследуется характеристическое уравнение

замкнутой САУ:

.

Коэффициенты этого уравнения являются функциями исследуемых параметров , :

 , . При изменении параметров a и b корни характеристического уравнения изменяют свое положение в плоскости корней комплексного переменного s.

        Переход из области устойчивости (левой полуплоскости) в область неустойчивости (правую полуплоскость) осуществляется при значении :

                                       .                                        (4.4)

Выделяя вещественную и мнимую части в (2.4) и приравнивая их к нулю, получим два уравнения:

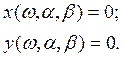                                                                                                                       (4.5)

Решая эти уравнения, определяем уравнение D-кривой в параметрической форме:

                                                            .                                               (4.6)

D-кривая строится в плоскости a, b при изменении  от 0 до . Для построения границ области устойчивости также используются особые кривые, которые получаются приравниваем к нулю коэффициентов  и : . Если коэффициенты  и  не зависят от параметров a и b, то особая линия уходит в бесконечность и на плоскости (a, b) не вычерчивается.

         Для определения области устойчивости используется правило штриховки. С этой же целью могут применяться критерии устойчивости.

         Рассматривается задача исследования устойчивости системы стабилизации угла рыскания ЛА с помощью сформулированных критериев и моделированием. Кроме того, с помощью метода  D-разбиения и моделированием строится область устойчивости в плоскости передаточных чисел  и  автопилота.

Исследование устойчивости с использованием критерия Гурвица и моделированием.

Рассмотрим систему стабилизации углового движения ЛА относительно центра масс в горизонтальной плоскости. В качестве программного движения принимается полет ЛА на заданной высоте с постоянной скоростью. Принимается, что динамика системы стабилизации угла рыскания описывается линейными дифференциальными уравнениями в отклонениях относительно программного движения:

                                                1)

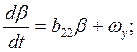
                                                2)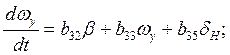                                                (4.7)

                                                3)

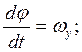
                                                4) 

где  – угол скольжения,  – угол рыскания, – угловая  скорость рыскания, – угол отклонения руля направления,  – известные динамические коэффициенты, определяемые аналогично коэффициентам  в системе (1.30), ,  
– передаточные числа автопилота,   – известная функция, задающая программу угла рыскания.

В системе уравнений индекс  отклонений от программных значений опущен. Значения динамических коэффициентов для различных вариантов представлены в табл.2.1. Уравнения 1) – 3)  описывают динамику ЛА, 4) – систему управления. При этом рулевая машинка считается безинерционной.

Таблица  4.1

варианты	b22	b32	b33	b35	i1	i2
1	-1,0	-3,50	-0,9	2,5	2	1
2	-1,5	-4,0	-1,0	4,0	2	0,4
3	-0,7	-2,0	-0,7	2,4	1,2	0,3
4	-1,2	-3,7	-0,9	3,2	2,0	1,4
5	-1,1	-3,4	-1,3	3,2	4,0	0,3
6	-1,4	-4,1	-1,15	4,7	2,0	0,4
7	-1,6	-4,5	-1,6	5,4	1,0	0,2
8	-1,5	-1,2	-1,5	3,0	1,2	0,5
9	-1,4	-1,3	-1,3	3,3	1	0,5
10	-1,3	-1,4	-1,1	3,2	1	0,4
11	-1,2	-1,3	-1,3	3,0	2	0,3
12	-1,05	-1,0	-2,4	8,0	1,3	0,8
13	-1,5	-2,4	-2,0	4,0	1	0,6
14	-2,0	-4,5	-0,5	2,5	1	0,6
15	-1,7	-3,8	-1,4	3,6	1,8	0,5
16	-1,6	-3,6	-1,2	3,4	1,9	0,4
17	-1,5	-3,5	-1,0	3,2	1,8	0,4
18	-1,4	-3,2	-0,9	3,0	1,7	0,6
19	-1,3	-3,0	-0,8	2,9	1,6	0,7
20	-1,2	-2,8	-0,8	2,8	1,5	0,8
21	-1,1	-2,6	-0,7	2,7	1,4	0,5
22	-1,0	-2,4	-1,2	2,6	1,2	0,4
23	-1,2	-3,2	-0,8	3,0	1,1	0,45
24	-1,3	-3,4	-0,9	3,2	1,1	0,5
25	-1,4	-3,6	-1,0	3,1	1,2	0,6