Электротехника \ Электронные устройства

Исследование переходных процессов и качества регулирования САУ. Исследование устойчивости САУ, страница 3

Численные значения коэффициентов приведены в табл.1.1, некоторые значения коэффициентов взяты из работ [8,9]. Значения коэффициентов , , , приведены в табл.1.2.

Т а б л и ц а 1.1

Варианты
1	-0,73	-2,02	-0,68	2,41	1,2	0,3
2	-1,15	-3,75	-0,94	3,18	2,0	1,3
3	-1,13	-3,14	-1,28	3,20	4,0	0,3
4	-1,39	-4,10	-1,14	4,72	2,0	0,4
5	-1,61	-4,50	-1,65	5,40	1,0	0,4
6	-1,0	-3,50	-0,90	2,5	2	1
7	-1,5	-4	-1,0	4,0	2	1
8	-1,4	-4	-1,2	5,0	2	0,5
9	-1,2	-1,3	-1,3	3,0	2	0,3
10	-1,3	-1,4	-1,1	3,2	1	0,4
11	-1,4	-1,3	-1,3	3,3	1	0,5
12	-1,5	-1,2	-1,5	3,0	1,2	0,5
13	-1,6	-1,0	-1,4	3,5	1,5	0,8
14	-1,35	-1,2	-1,5	4,0	1	0,8
15	-2,0	-1,5	-1,2	3,0	1,2	0,6
16	-1,0	-2,4	-0,7	2,6	1,2	0,4
17	-1,1	-2,6	-0,8	2,7	1,4	0,45
18	-1,2	-2,8	-0,8	2,8	1,5	0,50
19	-1,3	-3,0	-0,8	2,9	1,6	0,50
20	-1,4	-3,2	-0,9	3,0	1,7	0,50
21	-1,5	-3,5	-1,0	3,2	1,8	0,4
22	-1,6	-3,6	-1,2	3,4	1,9	0,4
23	-1,7	-3,8	-1,4	3,6	1,8	0,35
24	-2,0	-4,5	-0,5	2,5	1	0,6
25	-1,5	-6,5	-2,0	4,0	1	0,6
26	-1,05	-10	-2,4	8,0	1,3	0,8
27	-0,6	-3,0	-0,5	2,3	1	0,4
28	-0,65	-3,1	-,9	2,6	1,2	0,5
29	-0,75	-2,4	-1,0	3,0	1,1	0,6
30	-1,1	-10	-1,2	2,8	1,2	0,5

Т а б л и ц а 1.2

	Кс	Тс		T1с
1	0.6991	0.6304	0.4444	1.3699
2	0.7570	0.4550	0.4754	0.8696
3	0.7884	0.4669	0.5627	0.8850
4	1.1541	0.4194	0.5306	0.7194
5	1.2148	0.3738	0.6093	0.6211
6	0.5682	0.4767	0.4529	1.0000
7	1.0909	0.4264	0.5330	0.6667
8	1.2324	0.4196	0.5455	0.7143
9	1.2587	0.5913	0.7391	0.8333
10	1.4700	0.5944	0.7133	0.7692
11	1.4808	0.5661	0.7643	0.7143
12	1.3043	0.5384	0.8076	0.6667
13	1.7284	0.5556	0.8333	0.6250
14	1.6744	0.5568	0.7935	0.7407
15	1.5385	0.5064	0.8102	0.5000
16	0.8387	0.5680	0.4828	1.0000
17	0.8534	0.5361	0.5093	0.9091
18	0.8936	0.5157	0.5157	0.8333
19	0.9332	0.4975	0.5224	0.7692
20	0.9417	0.4735	0.5445	0.7143
21	0.9600	0.4472	0.5590	0.6667
22	0.9855	0.4256	0.5959	0.6250
23	0.9903	0.4023	0.6235	0.5882
24	0.9091	0.4264	0.5330	0.5000
25	0.6316	0.3244	0.5678	0.6667
26	0.6709	0.2826	0.4875	0.9524
27	0.4182	0.5505	0.3028	1.6667
28	0.4586	0.5209	0.4037	1.5385
29	0.7143	0.5634	0.4930	1.3333
30	0.2721	0.2972	0.3418	0.9091

Рассматривается задача определения весовых функций , соответствующих входу и выходам , и .

Весовые функции определяются моделированием, если на вход системы вместо подать -функцию:

На основании свойства − функции, определяемого соотношением (1.16), можно заменить воздействие в виде − функции начальными условиями. Весовые функции определяются моделированием системы:

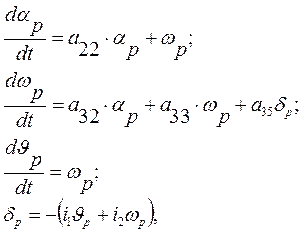(1.32)

с начальными условиями

; ; . (1.33)

Таким образом, для определения весовых функции ; ; , необходимо выполнить моделирование системы (1.32) с начальными условиями (1.33). Система дифференциальных уравнений решается методом Рунге-Кутта с постоянным шагом. По результатам моделирования строятся весовые функции:

Определение частотных характеристик замкнутой САУ.

Частотные характеристики исследуемой динамической системы, описываемой дифференциальными уравнениями (1.30), рассчитываются теоретически или определяются экспериментальными методами.

1 2 3 4 5 6

Скачать файл