Выбирая момент ![]() , получаем
, получаем ![]() .
Многомерная динамическая система, имеющая несколько входов и выходов, характеризуется
матрицей весовых функций:
.
Многомерная динамическая система, имеющая несколько входов и выходов, характеризуется
матрицей весовых функций:
![]() .
(1.19)
.
(1.19)
Весовой функцией ![]() , соответствующей
, соответствующей ![]() -му выходу и
-му выходу и ![]() -му
входу, называется реакция системы в момент
-му
входу, называется реакция системы в момент ![]() на
на
![]() -м выходе при действии в момент
-м выходе при действии в момент ![]() импульсного возмущения на
импульсного возмущения на ![]() -м входе. Весовые функции являются
важными характеристиками динамических систем и позволяют определить реакцию
системы на произвольные воздействия:
-м входе. Весовые функции являются
важными характеристиками динамических систем и позволяют определить реакцию
системы на произвольные воздействия:
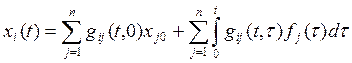 , (1.20)
, (1.20)
![]()
где ![]() фазовые
координаты;
фазовые
координаты; ![]() начальные условия;
начальные условия; ![]() входные воздействия.
входные воздействия.
Другими исчерпывающими характеристиками стационарной линейной системы являются ч а с т о т н ы е, которые определяют в установившемся режиме реакцию системы на гармоническое воздействие.
Если известна передаточная
функция системы ![]() , то частотная
характеристика
, то частотная
характеристика ![]() может быть найдена
аналитически и представляет собой передаточную функцию при чисто мнимых
значениях аргумента
может быть найдена
аналитически и представляет собой передаточную функцию при чисто мнимых
значениях аргумента ![]() :
:
![]() . (1.21)
. (1.21)
Частотная характеристика может быть
найдена методами моделирования. Для этого на вход системы подаётся
гармоническое воздействие частоты ![]() :
:
![]() .
(1.22)
.
(1.22)
Реакция система после окончания переходного процесса представляет собой также периодическую функцию
![]() ,
(1.23)
,
(1.23)
отличающуюся от входной функции по амплитуде и фазе, но имеющую ту же частоту:
![]() ,
(1.24)
,
(1.24)
![]() .
.
Таким способом определяются частотные характеристики реальных динамических систем, например, динамического стенда, полунатурных моделей, включающих в замкнутый контур элементы систем управления. Амплитуда входного воздействия должна выбираться так, чтобы динамика системы достаточно хорошо соответствовала линейной модели. При изменении амплитуды можно исследовать влияние нелинейностей на процессы в системе управления. Частотная амплитудно-фазовая характеристика системы или комплексный коэффициент усиления системы мы определяем выражением
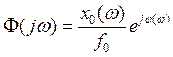 .
.
Здесь ![]() и
и
![]() − амплитуды выходной реакции системы
и входного воздействия;
− амплитуды выходной реакции системы
и входного воздействия; ![]() − разность фаз выходной реакции и входного
воздействия. При моделировании частота
− разность фаз выходной реакции и входного
воздействия. При моделировании частота ![]() изменяется
дискретно от 0 до достаточно большого значения
изменяется
дискретно от 0 до достаточно большого значения ![]() ,
которое определяется из физических соображений.
,
которое определяется из физических соображений.
Выражение для ![]() может быть представлено в виде
может быть представлено в виде
![]() (1.25)
(1.25)
или в виде
![]() .
(1.26)
.
(1.26)
Здесь ![]() − амплитудная частотная характеристика, равная
отношению амплитуд выходного и входного гармонических сигналов:
− амплитудная частотная характеристика, равная
отношению амплитуд выходного и входного гармонических сигналов:
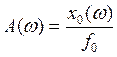 ,
(1.27)
,
(1.27)
![]() − фазовая частотная характеристика;
− фазовая частотная характеристика; ![]() − вещественная
частотная характеристика;
− вещественная
частотная характеристика; ![]() − мнимая частотная характеристика.
− мнимая частотная характеристика.
Для получения частотных характеристик экспериментальным путем для каждого значения частоты определяют амплитуду гармонического воздействия, амплитуду выходной величины, а также фазовый сдвиг между обоими колебаниями. Частотные характеристики могут быть получены как для замкнутых систем, так и для разомкнутых, а также для отдельных звеньев системы.
Метод частотных
характеристик является удобным аппаратом для исследования устойчивости и
качества регулирования. Частотная характеристика ![]() и
весовая функция связаны интегральными соотношениями (преобразование Фурье):
и
весовая функция связаны интегральными соотношениями (преобразование Фурье):
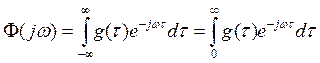 ;
(1.28)
;
(1.28)
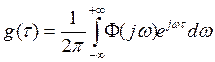 . (1.29)
. (1.29)
Рассмотрим систему стабилизации углового движения ЛА относительно ц.м. в продольной плоскости. В качестве программного движения принимается полет ЛА на заданной высоте с постоянной скоростью. Принимается, что динамика системы стабилизации описывается линейными дифференциальными уравнениями в отклонениях
относительно программного движения:
1) 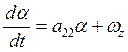 ;
;
2)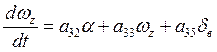 ;
(1.30)
;
(1.30)
3) 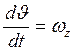 ;
;
4) ![]() ,
,
где ![]() − угол атаки,
− угол атаки, ![]() − угол тангажа,
− угол тангажа, ![]() − угловая скорость тангажа,
− угловая скорость тангажа, ![]() − угол отклонения руля высоты,
− угол отклонения руля высоты, ![]() − известные
динамические коэффициенты,
− известные
динамические коэффициенты, ![]() ,
, ![]() − передаточные
числа. Причем
− передаточные
числа. Причем
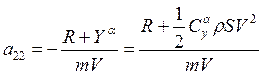 ,
,
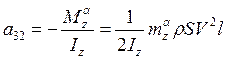 ,
,
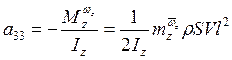 ,
,
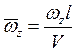 ,
,
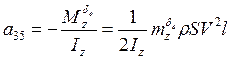 ,
,
где ![]() − тяга ЛА,
− тяга ЛА, ![]() − масса ЛА,
− масса ЛА,
![]() − момент
инерции ЛА,
− момент
инерции ЛА, ![]() ,
, ![]() ,
,
![]() ,
, ![]() − аэродинамические коэффициенты,
− аэродинамические коэффициенты, ![]() − массовая
плотность воздуха,
− массовая
плотность воздуха, ![]() − характерная площадь,
− характерная площадь, ![]() − характерная длина. В системе уравнений индекс
− характерная длина. В системе уравнений индекс ![]() отклонений от программных значений
опущен. Уравнения 1) − 3) описывают динамику
ЛА, уравнение 4) − уравнение системы управления.
При этом рулевая машинка считается безынерционной.
отклонений от программных значений
опущен. Уравнения 1) − 3) описывают динамику
ЛА, уравнение 4) − уравнение системы управления.
При этом рулевая машинка считается безынерционной.
Для получения передаточной функции (1.31) необходимо применить преобразование Лапласа к системе (1.30) и решить полученную систему алгебраических уравнений.
Передаточная функция ЛА,
характеризующая передачу воздействия от входа ![]() до
выхода
до
выхода ![]() , имеет вид
, имеет вид
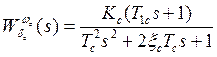 ,
(1.31)
,
(1.31)
где 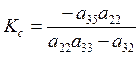 − коэффициент усиления ЛА;
− коэффициент усиления ЛА;
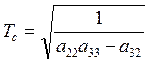 − постоянная времени ЛА;
− постоянная времени ЛА;
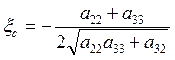 − коэффициент демпфирования;
− коэффициент демпфирования;
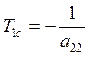 − постоянная времени форсирующего звена (скоростная
постоянная времени). Можно записать:
− постоянная времени форсирующего звена (скоростная
постоянная времени). Можно записать:
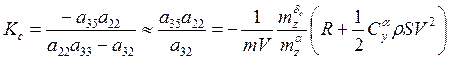 ,
,
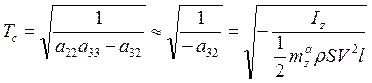 ,
,
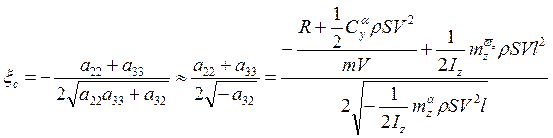 ,
,
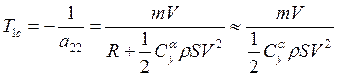 .
.
Из последних формул следует, что
коэффициент усиления ЛА ![]() увеличивается с
ростом скорости
увеличивается с
ростом скорости ![]() и уменьшается с ростом
коэффициента статической устойчивости
и уменьшается с ростом
коэффициента статической устойчивости 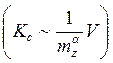 .
Величина коэффициента демпфирования
.
Величина коэффициента демпфирования ![]() почти не зависит
от скорости
почти не зависит
от скорости ![]() , но убывает с ростом высоты
, но убывает с ростом высоты ![]() . Таким образом собственное
демпфирование ЛА, особенно при подъеме на высоту, может оказаться недостаточным
для получения переходного процесса с заданным затуханием. Требуемое значение
. Таким образом собственное
демпфирование ЛА, особенно при подъеме на высоту, может оказаться недостаточным
для получения переходного процесса с заданным затуханием. Требуемое значение ![]() управляемого ЛА достигается выбором
параметров системы угловой стабилизации. Для баллистических ракет
управляемого ЛА достигается выбором
параметров системы угловой стабилизации. Для баллистических ракет ![]() . Для ЗУР
. Для ЗУР ![]() меняется
в пределах [0,35 – в начале полета до 0,08 – в конце полета]. Скоростная
постоянная времени
меняется
в пределах [0,35 – в начале полета до 0,08 – в конце полета]. Скоростная
постоянная времени ![]() уменьшается с увеличением
скорости
уменьшается с увеличением
скорости 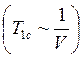 и резко увеличивается с ростом
высоты
и резко увеличивается с ростом
высоты 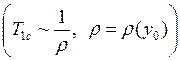 . При увеличении
. При увеличении ![]() ЛА становится более инерционным по
отношению к стремлению внешних сил изменить направление его движения.
Собственная частота ЛА
ЛА становится более инерционным по
отношению к стремлению внешних сил изменить направление его движения.
Собственная частота ЛА 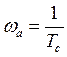 увеличивается с
ростом скорости
увеличивается с
ростом скорости ![]() , а с ростом высоты
уменьшается
, а с ростом высоты
уменьшается ![]() . Для маловысотных ЛА
. Для маловысотных ЛА ![]() , для большевысотных ЛА
, для большевысотных ЛА ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.