Составление математической модели полета неуправляемого летательного аппарата. Расчет дальности полета НЛА по параболической теории

2. Расчёт траектории неуправляемого РС

Во второй главе необходимо решить следующие задачи:

1.  составление математической модели полета неуправляемого летательного аппарата и решение ее.

2.  расчет дальности полета НЛА по параболической теории.

Для решения поставленных задач и получения траектории движения неуправляемого ЛА необходимо сначала задать исходные данные (параметры ЛА). Параметры неуправляемого ЛА (в системе СИ) в соответствии с вариантом задания на проектирование представлены в таблице 2.1:

По данным таблицы 2.1 рассчитываются все остальные необходимые параметры неуправляемого ЛА для расчета его траектории. Результаты этих расчетов представлены в таблице 2.2:

1. Секундный массовый расход q:

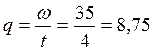 кг/с

2. Тяга двигателя R:

  

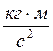
3. Коэффициент лобового сопротивления :

 

где  где  - коэффициент лобового сопротивления эталонного ЛА. Принимаем

где  =0,3

4. Площадь миделя ЛА S:

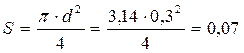 м²

5. Закон изменения массовой плотности воздуха от высоты полета принимаем в виде, где =1,23, высота над уровнем  моря Н=7800 м.

6. Закон изменения массы принимаем в виде

2.1 Модель  динамики   движения   по   направляющим,   на активном и пассивном участках траектории

Траектория полета неуправляемого ЛА (снаряда РСЗО) состоит из трех характерных участков:

1.  движение по направляющим;

2.  активный участок полет (когда работает двигательная установка);

3.  пассивный участок полета (когда двигательная установка не работает и снаряд движется, как свободно брошенное тело);

Для каждого из этих участков требуются свои начальные условия. Например, для пассивного участка полета начальными условиями будут являться параметры конца активного участка, в свою очередь, начальными условиями для активного будут являться параметры конца участка движения по направляющим.

Движение ЛА по направляющим

При расчете движения по направляющим принимается во внимание действие на ЛА следующих сил: R - тяга, G - вес ЛА, F - реакция направляющих, которая   состоит из силы трения F_тр и   нормальной составляющей N. Аэродинамическими силами при расчете движения по направляющим пренебрегают. В идеальном случае направляющая считается абсолютно жесткой, неподвижной, прямолинейной. ЛА схематизируется в виде точки. Расчетная схема представлена на рисунке:

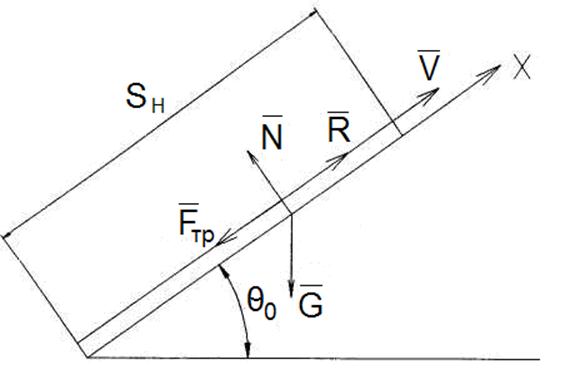
Запишем векторное уравнение движения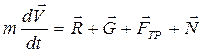

Уравнение движения ЛА по направляющим в проекциях на направление скорости запишется в виде:

, ,

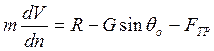где - коэффициент трения скольжения, - принимаем в работе закон изменения массы ЛА (для стали), .

1.  Рассмотрим случай, когда  

,

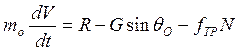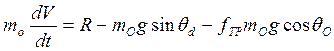
Далее интегрируя выражение, получаем

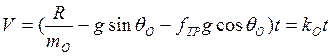
Учитывая, 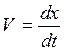 получаем

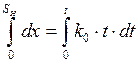
Находим  через длину направляющей , а потом V: 

; ;

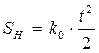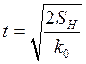2.  Рассмотрим случай, когда

, 

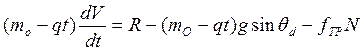
Отсюда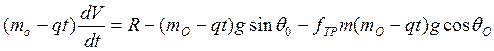

Здесь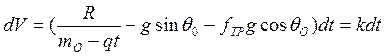

Проинтегрировав соотношение, получаем

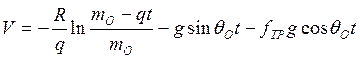
С учетом 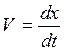, вычисляем

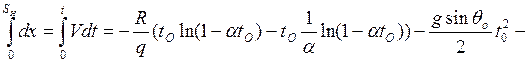
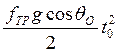
где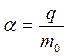

Полагая в формулах t=t₀ получаем выражение для дульной скорости V₀ и длины направляющих :

V_t=t0=V₀, S_t=t0=S_H

Если задана длина направляющих, то решая численно уравнение, определяем t₀. Если пренебречь изменением массы при движении ЛА по направляющим, то, заменяя массу ЛА средним значением m=m₀, получим

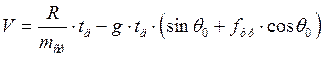
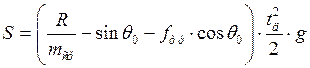
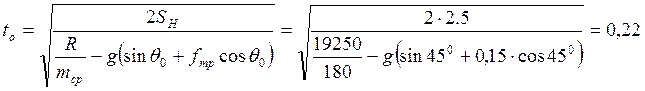 (c)

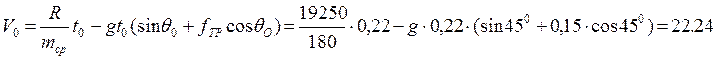 (м/с)

Результаты расчета приведены в таблице 2.3:

Дульная скорость V0, м/с	Дульное время , с	Угол наклона , град
22.24	0.22	45

Активный участок полета.

 При расчете траектории неуправляемого ЛА принимаемся за материальную точку переменной массы, которая совпадает с центром масс ЛА. Это эквивалентно допущению, что вращательное движение ЛА относительно центра масс не оказывает влияния на движение центра масс ЛА.

При расчете  активного участка полета ЛА принимают следующие допущения:

1.  угол атаки равен нулю;

2.  тяга R постоянна.

 При сделанных допущениях уравнения для расчета траектории ЛА на активном участке полета в проекции на касательную и нормаль к траектории запишутся    в виде следующей системы дифференциальных уравнений первого порядка:

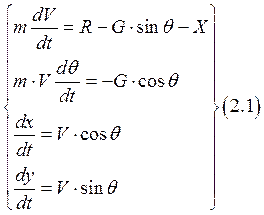
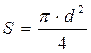Здесь - сила лобового сопротивления и - безразмерный коэффициент лобового сопротивления, - плотность воздуха, - площадь миделя соответственно.

Начальными условиями служат: , , , .

Система является нелинейной и точного аналитического решения не имеет.

Пассивный участок полета.

При расчете пассивного участка полета полагается что:

 1. тяга R равна нулю;

2. масса ЛА постоянна

Тогда уравнения активного участка переходят в уравнения пассивного участка:

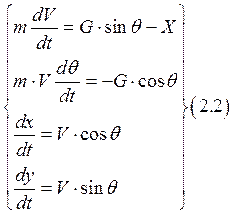
Уравнение интегрируется при начальных условиях , , ,

, где - время конца активного участка. Основным методом расчета полученной системы уравнений является численное интегрирование. Расчет ведется до тех пор, когда не выполнится условие =0.

2.2.  Методы и алгоритмы численного интегрирования

Метод Эйлера

Рассмотрим метод Эйлера - линейное приближение, использующее первые два члена ряда Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле 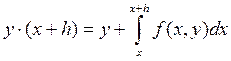 можно вычислить, используя теорему о среднем, т.е. вынося подынтегральную функцию из-под знака интеграла средним значением.

В методе Эйлера  подынтегральная функция выносится при нижнем пределе интегрирования: . Это приближение геометрически соответствует движению от точки х к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера:

, 

,